第一章 勾股定理单元质量检测试卷B(含答案)
文档属性
| 名称 | 第一章 勾股定理单元质量检测试卷B(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 21:08:09 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版2022-2023学年八年级(上)第一章勾股定理检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 如图所示,在 中,,,点 , 是中线 上的两点,则图中阴影部分的面积是
A. B. C. D.
2. 如图,若圆柱的底面周长是 ,高是 ,从圆柱底部 处沿侧面缠绕一圈丝线到顶部 处做装饰,则这条丝线的最小长度是
A. B. C. D.
3. 已知,如图长方形 中,,,将此长方形折叠,使点 与点 重合,折痕为 ,则 的面积为
A. B. C. D.
4. 丁明同学测量一个等腰三角形的腰、底边和底边上的高,得到了三个数据,但他把这三个数据与其它三组数据弄混了,请帮助丁明同学辨别.正确的数据所在的选项是
A. ,, B. ,, C. ,, D. ,,
5. 已知直角平面内点 ,,那么线段 的长等于
A. B. C. D.
6. 如图,在 中,,,, 是 的平分线.若 , 分别是 和 上的动点,则 的最小值是
A. B. C. D.
7. 正方体盒子的棱长为 , 的中点为 ,一只蚂蚁从点 爬行到点 的最短距离为
A. B. C. D.
8. 如图, 中,,,,将 折叠,使点 与 的中点 重合,折痕为 ,则线段 的长为
A. B. C. D.
9. 已知 , 是线段 上的两点,,,以点 为圆心, 长为半径画弧,再以点 为圆心, 长为半径画弧,两弧交于点 ,连接 ,,如图所示,则 一定是
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
10. 如图,在实践活动课上,小华打算测量学校旗杆的高度,她发现旗杆顶端的绳子垂到地面后还多出 ,当她把绳子斜拉直,且使绳子的底端刚好接触地面时,测得绳子底端距离旗杆底部 ,由此可计算出学校旗杆的高度是
A. B. C. D.
11. 如图是一个圆柱形饮料罐,底面半径是 ,高是 ,上底面的中心有一个小圆孔,已知一条到达底部的直吸管在罐内部分的长度为 ,若直吸管在罐外部分的长度为 ,则吸管的总长度 (罐壁的厚度和小圆孔的大小忽略不计)的取值范围是
A. B. C. D.
12. 【例 】如图,长方体的长为 ,宽为 ,高为 ,点 离点 的距离为 ,一只蚂蚁如果要沿着长方体的表面从点 爬到点 ,需要爬行的最短距离是
A. B. C. D.
二、填空题(共6小题;每小题4分,共24分)
13. 如图,在一个长为 米,宽为 米的纸板上有一长方体木块,它的长和纸板宽 平行且大于 ,木块的正面是边长为 米的正方形,一只蚂蚁从 处爬行到 处需要走的最短路程是 米.
14. 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图①所示)中各板块的边长之间的关系拼成一个凸六边形(如图②所示),则该凸六边形的周长是 .
15. 如图,在一款名为超级玛丽的游戏中,马里奥到达一个高为 米的高台 ,利用旗杆顶部的绳索划过 ,到达与高台 水平距离为 米,高为 米的矮台 ,马里奥在荡绳索过程中离地面的最低点的高度 .
16. 如图所示的网格是正方形网格,则 (点 ,, 是网格线的交点).
17. 如图, 中,,,,将 折叠,使点 与点 重合,折痕为 ,则 的周长等于 .
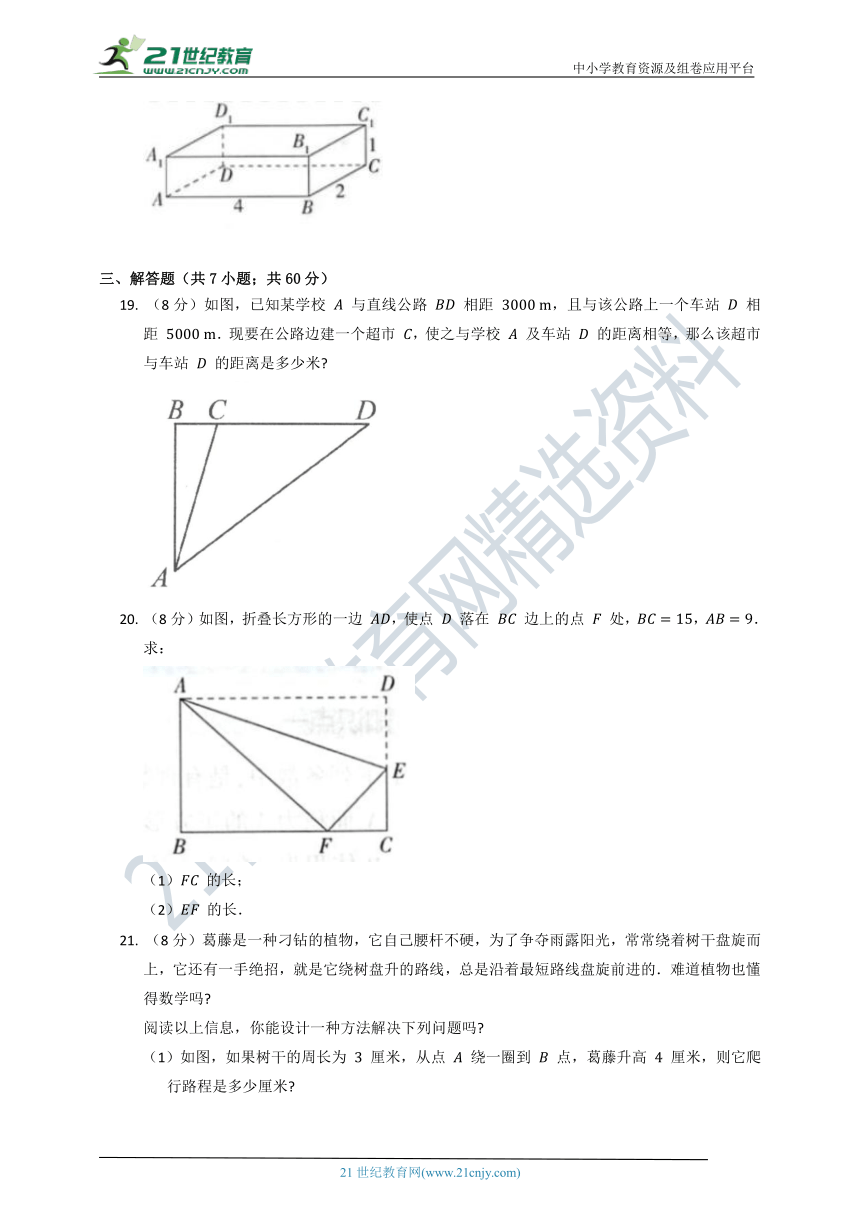
18. 如图,一只蚂蚁从实心长方体的顶点 出发,沿长方体的表面爬到对角顶点 处,蚂蚁爬行的最短距离为 .
三、解答题(共7小题;共60分)
19. (8分)如图,已知某学校 与直线公路 相距 ,且与该公路上一个车站 相距 .现要在公路边建一个超市 ,使之与学校 及车站 的距离相等,那么该超市与车站 的距离是多少米
20. (8分)如图,折叠长方形的一边 ,使点 落在 边上的点 处,,.
求:
(1) 的长;
(2) 的长.
21. (8分)葛藤是一种刁钻的植物,它自己腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线,总是沿着最短路线盘旋前进的.难道植物也懂得数学吗
阅读以上信息,你能设计一种方法解决下列问题吗
(1)如图,如果树干的周长为 厘米,从点 绕一圈到 点,葛藤升高 厘米,则它爬行路程是多少厘米
(2)如果树干的周长为 厘米,绕一圈爬行 厘米,则爬行一圈升高多少厘米 如果爬行 圈到达树顶,那么树干的高是多少厘米
22. (10分)如图,在 中, 是 边上一点,连接 ,若 ,,,.
(1)求 的度数;
(2)求 的长.
23. (10分)如图,在 中,,,,点 从点 出发,以每秒 的速度向点 运动,到 点停止.连接 ,设运动时间为 秒 .
(1)求 的面积;
(2)当 时,求 的值.
24. (8分)为筹备迎新晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图.已知圆筒的高为 ,其横截面周长为 ,如果在表面均匀缠绕油纸 圈,应裁剪多长的油纸
25. (8分)如图,长方形纸片 沿对角线 折叠,设点 落在 处, 交 于点 ,,,求阴影部分的面积.
答案
第一部分
1. A
【解析】,, 是 的中线,
,,
,,
,
故选:A.
2. D 【解析】圆柱的侧面展开图如图,连接 ,
则 的长即为丝线的最小长度.
由勾股定理得 ,
即 .
3. C
4. A
5. B
6. C
【解析】如图,过点 作 于点 ,交 于点 ,过点 作 于点 ,
是 的平分线,
,这时 有最小值,即 的长度,
,,,
,
,
,
即 的最小值为 .
7. A
【解析】将正方体展开,如图所示,连接 ,
因为点 是 的中点,
所以 ,
所以 ,
所以 .
蚂蚁从 点爬行到 点的最短距离为 .
8. A
【解析】设 ,由折叠的性质可得 ,
是 的中点,
,
在 中,,
解得 ,即 .
9. B
【解析】依据作图可以得到 ,,,
则 ,即可得出 是直角三角形.
10. C
11. D
【解析】如图,设圆柱底面圆的圆心为 ,连接 ,,
当吸管底部在 点时,吸管在罐内部分最短,即 的值最小,此时 ;
当吸管底部在 点时,吸管在罐内部分最长,此时 的值最大,
在 中,,故此时 ,
所以 ,
则吸管的总长度 (罐壁的厚度和小圆孔的大小忽略不计)的取值范围是 .
故选D.
12. B 【解析】将长方体展开,连接 ,,
根据两点之间线段最短,
()如图 ,
,,
由勾股定理得:.
()如图 ,
,,
由勾股定理得,.
()只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如图 :
长方体的宽为 ,高为 ,点 离点 的距离是 ,
,,
在直角三角形 中,根据勾股定理得:
;
由于 ,
故选:B.
第二部分
13.
【解析】如图,将木块看成是由纸片折成的,将其拉平成一个长方形,连接 ,
米, 米,
,
米,
妈蚁从 处爬行到 处需要走的最短路程为 米.
14.
15. 米
【解析】如图,作 ,,
,
,
在 和 中,
,
,,即 ,
,
,
,,
,
由勾股定理得 ,
,
马里奥在荡绳索过程中离地面的最低,点的高度 为 米.
16.
【解析】如图,延长 交网格线的边缘于 ,连接 ,
设每个小正方形的边长为 ,
则 ,,
,
,
,
.
17.
【解析】 中,,,,
,
将 折叠,使点 与点 重合,折痕为 ,
,
.
18.
【解析】分三种情况进行讨论:
①将四边形 与四边形 展开放在同一平面内.连接 ,如图 所示,
所走的最短路线显然为线段 ,
在 中,由勾股定理得 ;
②将四边形 与四边形 展开放在同一平面内.连接 ,如图 所示,
所走的最短路线显然为线段 ,
在 中,由勾股定理得 ;
③将四边形 与四边形 展开放在同一平面内.连接 ,如图 所示,
所走的最短路线显然为线段 ,
在 中,由勾股定理得 .
因为 ,
所以情况①的路线最短,故蚂蚁需要爬行的最短路程是 .
第三部分
19. 该超市与车站 的距离是 .
20. (1) 因为四边形 是长方形,
所以 ,
由折叠的性质可知 ,
在 中,由勾股定理得,,
所以 ,
的以 .
(2) 由折叠的性质可知 .
设 ,则 ,
在 中,由勾股定理得,,
即 ,解得 ,
即 的长为 .
21. (1) 如果树干的周长为 厘米,绕一圈升高 厘米,则葛藤绕树爬行的最短路线的长为 厘米.
(2) 如果树干的周长为 厘米,绕一圈爬行 厘米,则爬行一圈升高 厘米.
如果爬行 圈到达树顶,那么树干的高为 厘米.
22. (1) 在三角形 中,,,,
,
三角形 为直角三角形,且 .
(2) 由()知,,
,
三角形 为直角三角形,
,
,
.
23. (1) 在 中,,,,
,
.
(2) 设 ,则 ,
在 中,
,
由勾股定理,得:,
即 ,
解得:,
当点 运动到 时, 的值为 .
24. 如图为该灯罩的展开图,
在 中,
因为 ,(),
所以由勾股定理,得 ,
所以 ,
所以应裁剪 的油纸.
25. 在 和 中,
,,,
,
,
设 ,则 ,
在 中,,
即 ,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版2022-2023学年八年级(上)第一章勾股定理检测试卷B
(时间120分钟,满分120分)
一、选择题(共12小题;每小题3分,共36分)
1. 如图所示,在 中,,,点 , 是中线 上的两点,则图中阴影部分的面积是
A. B. C. D.
2. 如图,若圆柱的底面周长是 ,高是 ,从圆柱底部 处沿侧面缠绕一圈丝线到顶部 处做装饰,则这条丝线的最小长度是
A. B. C. D.
3. 已知,如图长方形 中,,,将此长方形折叠,使点 与点 重合,折痕为 ,则 的面积为
A. B. C. D.
4. 丁明同学测量一个等腰三角形的腰、底边和底边上的高,得到了三个数据,但他把这三个数据与其它三组数据弄混了,请帮助丁明同学辨别.正确的数据所在的选项是
A. ,, B. ,, C. ,, D. ,,
5. 已知直角平面内点 ,,那么线段 的长等于
A. B. C. D.
6. 如图,在 中,,,, 是 的平分线.若 , 分别是 和 上的动点,则 的最小值是
A. B. C. D.
7. 正方体盒子的棱长为 , 的中点为 ,一只蚂蚁从点 爬行到点 的最短距离为
A. B. C. D.
8. 如图, 中,,,,将 折叠,使点 与 的中点 重合,折痕为 ,则线段 的长为
A. B. C. D.
9. 已知 , 是线段 上的两点,,,以点 为圆心, 长为半径画弧,再以点 为圆心, 长为半径画弧,两弧交于点 ,连接 ,,如图所示,则 一定是
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
10. 如图,在实践活动课上,小华打算测量学校旗杆的高度,她发现旗杆顶端的绳子垂到地面后还多出 ,当她把绳子斜拉直,且使绳子的底端刚好接触地面时,测得绳子底端距离旗杆底部 ,由此可计算出学校旗杆的高度是
A. B. C. D.
11. 如图是一个圆柱形饮料罐,底面半径是 ,高是 ,上底面的中心有一个小圆孔,已知一条到达底部的直吸管在罐内部分的长度为 ,若直吸管在罐外部分的长度为 ,则吸管的总长度 (罐壁的厚度和小圆孔的大小忽略不计)的取值范围是
A. B. C. D.
12. 【例 】如图,长方体的长为 ,宽为 ,高为 ,点 离点 的距离为 ,一只蚂蚁如果要沿着长方体的表面从点 爬到点 ,需要爬行的最短距离是
A. B. C. D.
二、填空题(共6小题;每小题4分,共24分)
13. 如图,在一个长为 米,宽为 米的纸板上有一长方体木块,它的长和纸板宽 平行且大于 ,木块的正面是边长为 米的正方形,一只蚂蚁从 处爬行到 处需要走的最短路程是 米.
14. 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图①所示)中各板块的边长之间的关系拼成一个凸六边形(如图②所示),则该凸六边形的周长是 .
15. 如图,在一款名为超级玛丽的游戏中,马里奥到达一个高为 米的高台 ,利用旗杆顶部的绳索划过 ,到达与高台 水平距离为 米,高为 米的矮台 ,马里奥在荡绳索过程中离地面的最低点的高度 .
16. 如图所示的网格是正方形网格,则 (点 ,, 是网格线的交点).
17. 如图, 中,,,,将 折叠,使点 与点 重合,折痕为 ,则 的周长等于 .
18. 如图,一只蚂蚁从实心长方体的顶点 出发,沿长方体的表面爬到对角顶点 处,蚂蚁爬行的最短距离为 .
三、解答题(共7小题;共60分)
19. (8分)如图,已知某学校 与直线公路 相距 ,且与该公路上一个车站 相距 .现要在公路边建一个超市 ,使之与学校 及车站 的距离相等,那么该超市与车站 的距离是多少米
20. (8分)如图,折叠长方形的一边 ,使点 落在 边上的点 处,,.
求:
(1) 的长;
(2) 的长.
21. (8分)葛藤是一种刁钻的植物,它自己腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线,总是沿着最短路线盘旋前进的.难道植物也懂得数学吗
阅读以上信息,你能设计一种方法解决下列问题吗
(1)如图,如果树干的周长为 厘米,从点 绕一圈到 点,葛藤升高 厘米,则它爬行路程是多少厘米
(2)如果树干的周长为 厘米,绕一圈爬行 厘米,则爬行一圈升高多少厘米 如果爬行 圈到达树顶,那么树干的高是多少厘米
22. (10分)如图,在 中, 是 边上一点,连接 ,若 ,,,.
(1)求 的度数;
(2)求 的长.
23. (10分)如图,在 中,,,,点 从点 出发,以每秒 的速度向点 运动,到 点停止.连接 ,设运动时间为 秒 .
(1)求 的面积;
(2)当 时,求 的值.
24. (8分)为筹备迎新晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸,如图.已知圆筒的高为 ,其横截面周长为 ,如果在表面均匀缠绕油纸 圈,应裁剪多长的油纸
25. (8分)如图,长方形纸片 沿对角线 折叠,设点 落在 处, 交 于点 ,,,求阴影部分的面积.
答案
第一部分
1. A
【解析】,, 是 的中线,
,,
,,
,
故选:A.
2. D 【解析】圆柱的侧面展开图如图,连接 ,
则 的长即为丝线的最小长度.
由勾股定理得 ,
即 .
3. C
4. A
5. B
6. C
【解析】如图,过点 作 于点 ,交 于点 ,过点 作 于点 ,
是 的平分线,
,这时 有最小值,即 的长度,
,,,
,
,
,
即 的最小值为 .
7. A
【解析】将正方体展开,如图所示,连接 ,
因为点 是 的中点,
所以 ,
所以 ,
所以 .
蚂蚁从 点爬行到 点的最短距离为 .
8. A
【解析】设 ,由折叠的性质可得 ,
是 的中点,
,
在 中,,
解得 ,即 .
9. B
【解析】依据作图可以得到 ,,,
则 ,即可得出 是直角三角形.
10. C
11. D
【解析】如图,设圆柱底面圆的圆心为 ,连接 ,,
当吸管底部在 点时,吸管在罐内部分最短,即 的值最小,此时 ;
当吸管底部在 点时,吸管在罐内部分最长,此时 的值最大,
在 中,,故此时 ,
所以 ,
则吸管的总长度 (罐壁的厚度和小圆孔的大小忽略不计)的取值范围是 .
故选D.
12. B 【解析】将长方体展开,连接 ,,
根据两点之间线段最短,
()如图 ,
,,
由勾股定理得:.
()如图 ,
,,
由勾股定理得,.
()只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如图 :
长方体的宽为 ,高为 ,点 离点 的距离是 ,
,,
在直角三角形 中,根据勾股定理得:
;
由于 ,
故选:B.
第二部分
13.
【解析】如图,将木块看成是由纸片折成的,将其拉平成一个长方形,连接 ,
米, 米,
,
米,
妈蚁从 处爬行到 处需要走的最短路程为 米.
14.
15. 米
【解析】如图,作 ,,
,
,
在 和 中,
,
,,即 ,
,
,
,,
,
由勾股定理得 ,
,
马里奥在荡绳索过程中离地面的最低,点的高度 为 米.
16.
【解析】如图,延长 交网格线的边缘于 ,连接 ,
设每个小正方形的边长为 ,
则 ,,
,
,
,
.
17.
【解析】 中,,,,
,
将 折叠,使点 与点 重合,折痕为 ,
,
.
18.
【解析】分三种情况进行讨论:
①将四边形 与四边形 展开放在同一平面内.连接 ,如图 所示,
所走的最短路线显然为线段 ,
在 中,由勾股定理得 ;
②将四边形 与四边形 展开放在同一平面内.连接 ,如图 所示,
所走的最短路线显然为线段 ,
在 中,由勾股定理得 ;
③将四边形 与四边形 展开放在同一平面内.连接 ,如图 所示,
所走的最短路线显然为线段 ,
在 中,由勾股定理得 .
因为 ,
所以情况①的路线最短,故蚂蚁需要爬行的最短路程是 .
第三部分
19. 该超市与车站 的距离是 .
20. (1) 因为四边形 是长方形,
所以 ,
由折叠的性质可知 ,
在 中,由勾股定理得,,
所以 ,
的以 .
(2) 由折叠的性质可知 .
设 ,则 ,
在 中,由勾股定理得,,
即 ,解得 ,
即 的长为 .
21. (1) 如果树干的周长为 厘米,绕一圈升高 厘米,则葛藤绕树爬行的最短路线的长为 厘米.
(2) 如果树干的周长为 厘米,绕一圈爬行 厘米,则爬行一圈升高 厘米.
如果爬行 圈到达树顶,那么树干的高为 厘米.
22. (1) 在三角形 中,,,,
,
三角形 为直角三角形,且 .
(2) 由()知,,
,
三角形 为直角三角形,
,
,
.
23. (1) 在 中,,,,
,
.
(2) 设 ,则 ,
在 中,
,
由勾股定理,得:,
即 ,
解得:,
当点 运动到 时, 的值为 .
24. 如图为该灯罩的展开图,
在 中,
因为 ,(),
所以由勾股定理,得 ,
所以 ,
所以应裁剪 的油纸.
25. 在 和 中,
,,,
,
,
设 ,则 ,
在 中,,
即 ,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
