4.2.3 线段的性质及其应用 教案
图片预览


文档简介
中小学教育资源及组卷应用平台
4.2.3 线段的性质及其应用 教学设计
课题 4.2.3 线段的性质及其应用 单元 第4 单元 学科 数学 年级 七年级(上)
教材分析 两点之间线段最短这一性质是度量的基础,在生产实际中经常要用到,这节课主要是让学生体验两点之间线段最短这一性质以及两点间距离的概念.
核心素养分析 经历从具体事例抽象出性质,再根据性质应用到具体事例的活动过程,体会从具体到抽象,再由抽象到具体的辩证关系.
学习目标 1.知道两点间的距离的含义,掌握“两点之间,线段最短”的性质并能运用.2.经历观察、实验、猜想等数学活动,发展合情推理能力,能有条理地、清晰地阐述自己的观点.
重点 知道两点间的距离的含义,掌握“两点之间,线段最短”的性质并能运用.
难点 理解两点之间线段最短,并能运用这一基本事实解决问题.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题)情境1:如图4-2.3-1,(1)绿地里本没有路,走的人多了……你能解释一下原因何在?为什么要建隧道?情境2:数学活动:在纸上任意画出两点,用线连接它们,量一下它们的长短,比较哪个最短?. 思考探究,获取新知问题1:最短路径.如图4-2.3-2(1),从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短的道路?如果能,请你联系以前所学过的知识,在图上画出最短路线.问题2:河道长度.如图4-2.3-2(2),把原来弯曲的河道改直,A,B两地间的河道长度有什么变化?问题3:九曲桥.如图4-2.3-2(3),公园里设计了曲折迂回的桥,这样做对游人观赏湖面风光有什么影响?与修一座笔直的桥相比,这样做是否增加了游人在桥上行走的路程?说出其中的道理.教师提问:你还能举出一些类似的例子吗?教师指导,学生阅读教材相关内容并总结.(1)两点之间,线段最短;(2)两点的距离:连接两点间的线段的长度. 思考自议引导学生发现两点间线段最短的特征。毛 从实际生活出发激发学生的兴趣,让学生欣赏并体会最短路线,培养学生的鉴别能力和正确的选择能力。
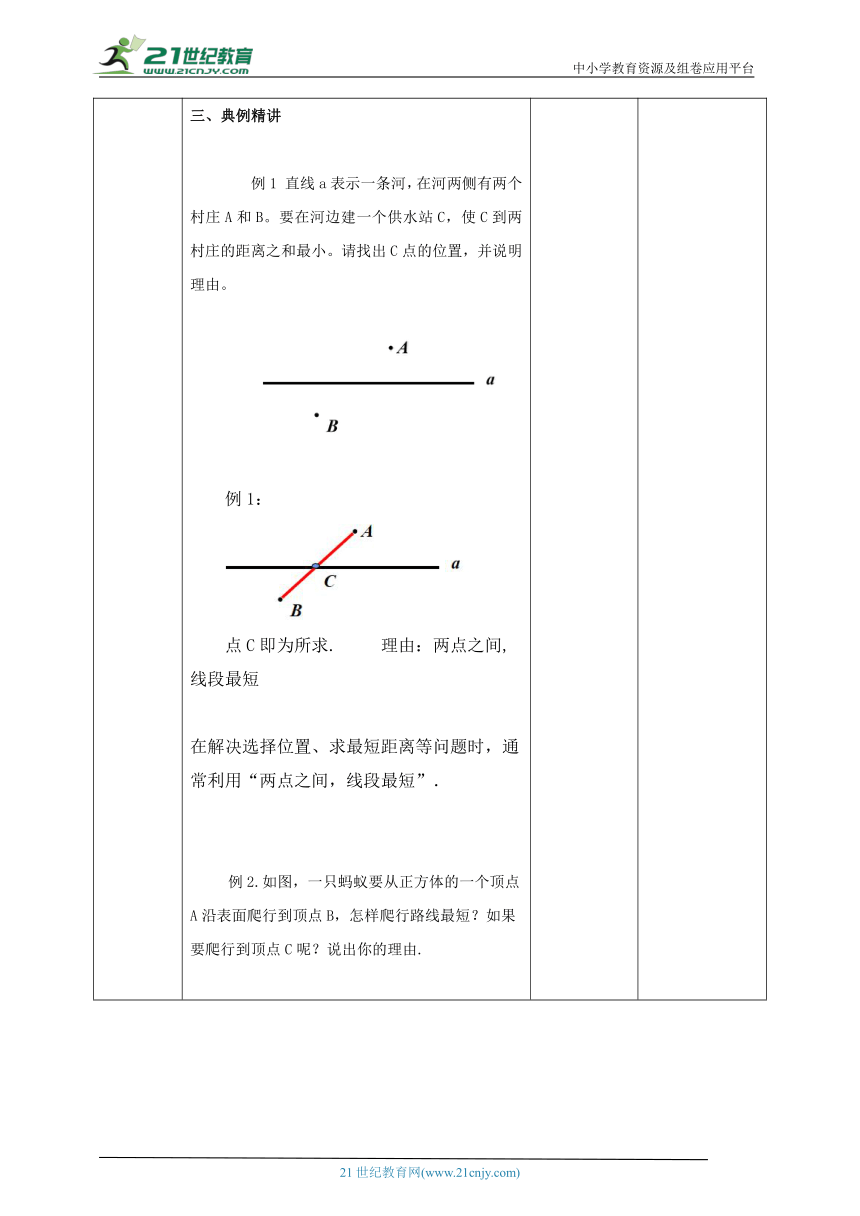
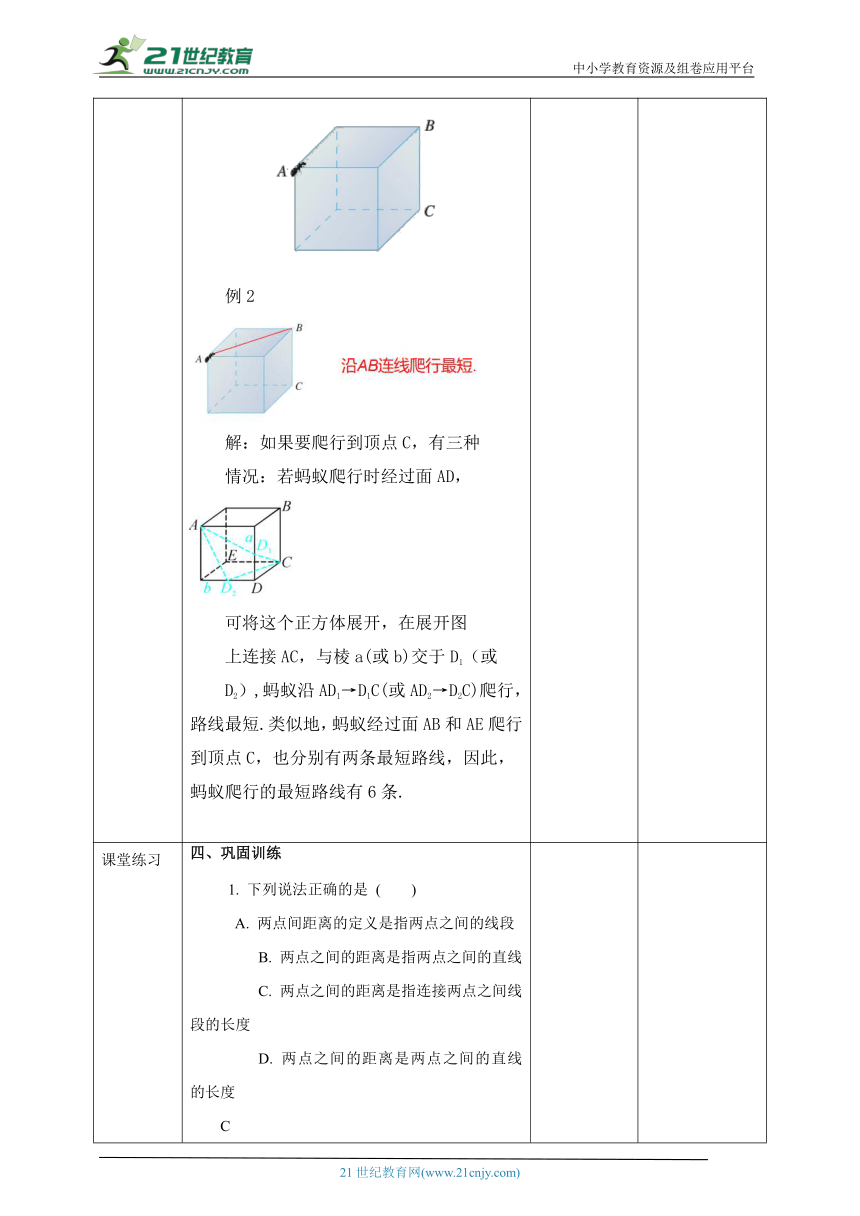
讲授新课 提炼概念 总结:距离不是线段.线段是一个几何图形;距离是一个量,它反映的是线段的长短.距离是一个数量且有长度单位.典例精讲例1 直线a表示一条河,在河两侧有两个村庄A和B。要在河边建一个供水站C,使C到两村庄的距离之和最小。请找出C点的位置,并说明理由。例1:点C即为所求. 理由:两点之间,线段最短在解决选择位置、求最短距离等问题时,通常利用“两点之间,线段最短”. 例2.如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点B,怎样爬行路线最短?如果要爬行到顶点C呢?说出你的理由. 例2 解:如果要爬行到顶点C,有三种情况:若蚂蚁爬行时经过面AD,可将这个正方体展开,在展开图上连接AC,与棱a(或b)交于D1(或D2),蚂蚁沿AD1→D1C(或AD2→D2C)爬行,路线最短.类似地,蚂蚁经过面AB和AE爬行到顶点C,也分别有两条最短路线,因此,蚂蚁爬行的最短路线有6条. 在学习中学会合作,在深入思考和交流讨论中获得感悟。 让学生在体验中思考,在讨论中交流。鼓励学生独立而富有个性的学习,倡导主动参与。
课堂练习 四、巩固训练 1. 下列说法正确的是 ( ) A. 两点间距离的定义是指两点之间的线段 B. 两点之间的距离是指两点之间的直线 C. 两点之间的距离是指连接两点之间线段的长度 D. 两点之间的距离是两点之间的直线的长度C2 如图所示,由M到N有①②③④共4条路线,最短的路线选①的理由是( ) A.因为它是直线 B.两点确定一条直线 C.两点之间的距离 D.两点之间,线段最短 D3.下列说法正确的是( ) A.两点之间,直线最短 B.线段MN就是M,N两点间的距离 C.在连接两点的所有线中,最短的连线的长度就是这两点间的距离 D.从武汉到北京,火车行走的路程就是武汉到北京的距离C4.下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程.其中可用基本事实“两点之间,线段最短”来解释的现象有( ) A. ①② B.①③ C.②④ D.③④D5.已知A、B、C三点在同一直线上,如果线段AB=6 cm,BC=3 cm,A、C两点的距离为d,那么( ) A.d=9cm B.d=3cm C.d=9cm或d=3cm D.d大小不确定C6.如下图,设A、B、C、D为4个居民小区,现在要在居民小区内建一个购物中心,试问把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小?说明理由。 7.A是锐角MON内部任意一点,在∠MON的两边OM,ON上各取一点B,C,组成三角形,使三角形周长最小。(如图所示) 解:作A与OM的 ( http: / / www.21cnjy.com )对称点D,再作A与ON的对称点E。连接DE(如图所示),据上题铺垫,我们可得,AB=BD,AC=CE,又因为D,B,C,E在一条直线上,所以,这时的周长是最短的。
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
4.2.3 线段的性质及其应用 教学设计
课题 4.2.3 线段的性质及其应用 单元 第4 单元 学科 数学 年级 七年级(上)
教材分析 两点之间线段最短这一性质是度量的基础,在生产实际中经常要用到,这节课主要是让学生体验两点之间线段最短这一性质以及两点间距离的概念.
核心素养分析 经历从具体事例抽象出性质,再根据性质应用到具体事例的活动过程,体会从具体到抽象,再由抽象到具体的辩证关系.
学习目标 1.知道两点间的距离的含义,掌握“两点之间,线段最短”的性质并能运用.2.经历观察、实验、猜想等数学活动,发展合情推理能力,能有条理地、清晰地阐述自己的观点.
重点 知道两点间的距离的含义,掌握“两点之间,线段最短”的性质并能运用.
难点 理解两点之间线段最短,并能运用这一基本事实解决问题.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题)情境1:如图4-2.3-1,(1)绿地里本没有路,走的人多了……你能解释一下原因何在?为什么要建隧道?情境2:数学活动:在纸上任意画出两点,用线连接它们,量一下它们的长短,比较哪个最短?. 思考探究,获取新知问题1:最短路径.如图4-2.3-2(1),从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短的道路?如果能,请你联系以前所学过的知识,在图上画出最短路线.问题2:河道长度.如图4-2.3-2(2),把原来弯曲的河道改直,A,B两地间的河道长度有什么变化?问题3:九曲桥.如图4-2.3-2(3),公园里设计了曲折迂回的桥,这样做对游人观赏湖面风光有什么影响?与修一座笔直的桥相比,这样做是否增加了游人在桥上行走的路程?说出其中的道理.教师提问:你还能举出一些类似的例子吗?教师指导,学生阅读教材相关内容并总结.(1)两点之间,线段最短;(2)两点的距离:连接两点间的线段的长度. 思考自议引导学生发现两点间线段最短的特征。毛 从实际生活出发激发学生的兴趣,让学生欣赏并体会最短路线,培养学生的鉴别能力和正确的选择能力。
讲授新课 提炼概念 总结:距离不是线段.线段是一个几何图形;距离是一个量,它反映的是线段的长短.距离是一个数量且有长度单位.典例精讲例1 直线a表示一条河,在河两侧有两个村庄A和B。要在河边建一个供水站C,使C到两村庄的距离之和最小。请找出C点的位置,并说明理由。例1:点C即为所求. 理由:两点之间,线段最短在解决选择位置、求最短距离等问题时,通常利用“两点之间,线段最短”. 例2.如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点B,怎样爬行路线最短?如果要爬行到顶点C呢?说出你的理由. 例2 解:如果要爬行到顶点C,有三种情况:若蚂蚁爬行时经过面AD,可将这个正方体展开,在展开图上连接AC,与棱a(或b)交于D1(或D2),蚂蚁沿AD1→D1C(或AD2→D2C)爬行,路线最短.类似地,蚂蚁经过面AB和AE爬行到顶点C,也分别有两条最短路线,因此,蚂蚁爬行的最短路线有6条. 在学习中学会合作,在深入思考和交流讨论中获得感悟。 让学生在体验中思考,在讨论中交流。鼓励学生独立而富有个性的学习,倡导主动参与。
课堂练习 四、巩固训练 1. 下列说法正确的是 ( ) A. 两点间距离的定义是指两点之间的线段 B. 两点之间的距离是指两点之间的直线 C. 两点之间的距离是指连接两点之间线段的长度 D. 两点之间的距离是两点之间的直线的长度C2 如图所示,由M到N有①②③④共4条路线,最短的路线选①的理由是( ) A.因为它是直线 B.两点确定一条直线 C.两点之间的距离 D.两点之间,线段最短 D3.下列说法正确的是( ) A.两点之间,直线最短 B.线段MN就是M,N两点间的距离 C.在连接两点的所有线中,最短的连线的长度就是这两点间的距离 D.从武汉到北京,火车行走的路程就是武汉到北京的距离C4.下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程.其中可用基本事实“两点之间,线段最短”来解释的现象有( ) A. ①② B.①③ C.②④ D.③④D5.已知A、B、C三点在同一直线上,如果线段AB=6 cm,BC=3 cm,A、C两点的距离为d,那么( ) A.d=9cm B.d=3cm C.d=9cm或d=3cm D.d大小不确定C6.如下图,设A、B、C、D为4个居民小区,现在要在居民小区内建一个购物中心,试问把购物中心建在何处,才能使4个居民小区到购物中心的距离之和最小?说明理由。 7.A是锐角MON内部任意一点,在∠MON的两边OM,ON上各取一点B,C,组成三角形,使三角形周长最小。(如图所示) 解:作A与OM的 ( http: / / www.21cnjy.com )对称点D,再作A与ON的对称点E。连接DE(如图所示),据上题铺垫,我们可得,AB=BD,AC=CE,又因为D,B,C,E在一条直线上,所以,这时的周长是最短的。
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
