专题2.7 二次根式 课件(共56张PPT)
文档属性
| 名称 | 专题2.7 二次根式 课件(共56张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 10:00:48 | ||
图片预览










文档简介
(共56张PPT)
八上数学同步精优课件
北师大版八年级上册
第二章 实数
2.7 二次根式
精优教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、掌握二次根式的概念,最简二次根式的概念;
2、运用二次根式的有意义条件解决有关问题;
3、掌握二次根式乘除法运算,熟练掌握二次根式乘除法法则;
4、掌握二次根式加减法运算,熟练掌握二次根式加减法法则;
导入新课
温故知新
1、什么叫做平方根
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根。
2、什么叫算术平方根
一般地,如果一个非负数的平方等于a,那么这个正数叫做a的算术平方根。
问题:如图,正方形ABCD的边长为2,它的对角线AC
的长是多少?
乙同学:
甲同学:
O
讲授新课
知识点一 二次根式的概念及有意义的条件
50米
a米
塔座所形成的这个直角三角形的
斜边长为______________米。
塔座
米
如图示的值表示正方形的面积,则
正方形的边长是
b-3
a叫被开方数
2. a可以是数,也可以是式;
3. 形式上含有二次根号 ;
5. 既可表示开平方运算,也可表示运算的结果.
1. 表示a的算术平方根;
( 双重非负性);
二次根式的特点:
典例精析
⑴
⑵
(3)
(4) .
,
例1:判断下列式中哪些是二次根式.
,
解:(1)、(3)、(4)是二次根式,(2)不是二次根式.
解:由x-2≥0,得
x≥2.
例2 (1)当x取何值时, 在实数范围内有意义
当x≥2时, 在实数范围内有意义.
当x=9时,
A. x>1 B. x>-1 C. x ≥1 D. x ≥-1
A
(2)当x=0,9时,求二次根式 的值.
(3)要使式子 有意义,则x的取值范围是( )
当x=0时,x-2=-2<0,此时二次根式无意义;
要使二次根式在实数范围内有意义,即需满足被开方数≥0,列不等式求解即可.若二次根式处在分母的位置,应同时考虑分母不为零.
归纳
练一练
1.x取何值时,下列二次根式有意义
求二次根式中字母的取值范围的依据:
1.根号内的式子是非负数。
2.若含有分母,则分母不为零.
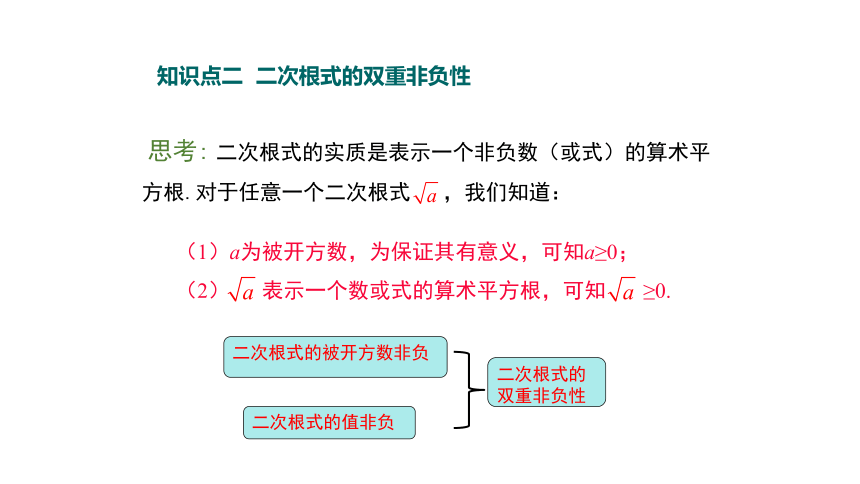
知识点二 二次根式的双重非负性
思考: 二次根式的实质是表示一个非负数(或式)的算术平方根.对于任意一个二次根式 ,我们知道:
(1)a为被开方数,为保证其有意义,可知a≥0;
(2) 表示一个数或式的算术平方根,可知 ≥0.
二次根式的被开方数非负
二次根式的值非负
二次根式的双重非负性
典例精析
(2)设 ,试求2x+y的值.
例3(1)若 ,求a -b+c的值.
解:
(1)由题意可知a-2=0,b-3=0,c-4=0,解得a=2,b=3,c=4
所以a-b+c=2-3+4=3;
(2)由题意知,1-x≥0,且x-1≥0,联立解得x=1.从而知y=2017,
所以2x+y=2×1+2017=2019.
多个非负数的和为零,则可得每个非负数均为零.初中阶段学过的非负数主要有绝对值、偶次幂及二次根式.
归纳
知识点三 二次根式的性质与化简
问题:观察比较
积的算术平方根的性质
两个非负数的积的算术平方根等于这两个非负数的算术平方根的积
=
=
=
那么 与 是否相等 ?
要点归纳
(a≥0,b≥0)
,
(a≥0, b>0).
商的算术平方根等于算术平方根的商
积的算术平方根等于算术平方根的积
典例精析
例4:化简
解:(1)
(2)
(3)
(1) ;(2) ;(3) .
最简二次根式:
一般地,被开方数不含分母,也不含能开得尽方的因数或因式,这样的二次根式,叫做最简二次根式.
最简二次根式的条件:
①是二次根式;
②被开方数中不含分母;
③被开方数中不含能开得尽方的因数或因式.
练一练
1:化简:
解:
知识点四 二次根式的乘除法运算
根据什么法则化成
还记得吗
(a≥0,b≥0),
(a≥0,b>0).
二次根式的乘法法则和除法法则
典例精析
例5:计算:
练一练
1:计算:
1.试回顾如何计算3a2·2a3= .
还记得单项式乘以单项式的法则吗?
2. 如何计算呢?
6a5
解:
归纳总结
二次根式的乘法扩充法则
第一步:根号外的系数与系数相乘,积为结果的系数;
第二步:根式和根式按公式相乘.
利用它可以进行二次根式的化简.
想一想
知识点五 二次根式的加减运算
(2)x2+2x2+4y= ;
1.(1)3x2+2x2= ;
2.类比合并同类项的方法,想想如何计算:
解:
3. 能不能再进行计算 为什么
答:不能,因为它们都是最简二次根式,被开方数不相同,所以不能合并.
5x2
3x2+4y
合作探究
同样,二次根式也可以进行加减运算,这时,以前学习的实数的运算法则、运算律仍然适用.当然,如果运算结果中出现某些项,它们各自化简后的被开方数相同,那么应当将这些项合并.
典例精析
解: (1)原式=
例5:计算:
(2)原式=
(3)原式=
练一练
解: (1)原式=
1:计算:
(2)原式=
(3)原式=
(4)原式=
归纳总结
二次根式的加减法法则
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
要点提醒
1.加减法的运算步骤:“一化简二判断三合并”.
2.合并的前提条件:只有被开方数相同的最简二次根式才能进行合并.
知识点六 二次根式的化简求值
下列每组二次根式化成最简二次根式,有什么特点?
与
与
几个二次根式化成最简二次根式后,如果它们的被开方式相同,那么,它们是同类二次根式。
说明:(1)必须是最简二次根式
(2)根指数与被开方数相同
(3)与二次根式的系数无关
与
被开方式相同
交流与发现
要用栅栏围成两个相邻的正方形羊圈,它们的面积分别为27平方米和48平方米,栅栏的长度为多少米?
小羊圈
大羊圈
这两个正方形的边分别为 米 米,栅栏的长度为(3 +4 )米
你能把3 +4 进一步化简吗?
几个二次根式化成最简二次根式后,如果它们的被开方式相同,那么,它们是同类二次根式。
说明:(1)必须是最简二次根式
(2)根指数与被开方数相同
(3)与二次根式的系数无关。
化简
,
3
3
3
3
27
2
=
×
=
3
4
3
4
48
2
=
×
=
典例精析
例6:已知 ,求
解析:先化简已知条件,再利用乘法公式变形,即a2+b2=(a+b)2-2ab,最后代入求解.
解:
练一练
1.如果最简二次根式 与 是同类二次根式,求m、n 的值.
解:由题意,得
m+n-2=2
m-n =2
∴ m=3 , n =1
2:计算:
解:
(1)
(2)
解法一:
(3)
你还有其他解法吗?
解法二: 原式=
解: (4)原式=
思考:还可以继续化简吗?为什么?
如果算式当中有个别二次根式化简最简二次根式仍不能与其它最简二次根式合并同类项,结果中可保留,不必化为最简式.
提醒
知识点七 二次根式的加减运算
例7:教师节就要到了,李欣同学准备做两张大小不同的正方形贺卡送给老师以表示祝贺,其中一张面积为288平方厘米,另一张面积为338平方厘米.如果用彩带把贺卡镶边会更漂亮,她现在有1.5米的彩带,请你帮忙算一算她的彩带够不够用.
解析:可以通过两个正方形的面积分别计算出正方形的边长,进一步求出两个正方形的周长之和,与1.5米比较即可得出结论.
解:贺卡的周长为
答:李欣的彩带够用.
练一练
1.在一个边长为 cm的正方形内部,挖去一个边长为 cm的正方形,求剩余部分的面积.
解:由题意得,
即剩余部分的面积是
当堂练习
课堂小结
(1)二次根式的性质
(2)最简二次根式的定义
(3)二次根式值的化简
二次根式的乘法法则和除法法则:
算术平方根的积等于各个被开方数积的算术平方根
两个二次根式相除,将它们的被开方数相除的商作为商的被开方数
同类二次根式:
(1)必须是最简二次根式
(2)根指数与被开方数相同
(3)与二次根式的系数无关
二次根式的加减实质是合并同类二次根式
法则:同类二次根式的系数相加减,做为结果的系数,根号及被开方术都不变
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精优课件
北师大版八年级上册
第二章 实数
2.7 二次根式
精优教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、掌握二次根式的概念,最简二次根式的概念;
2、运用二次根式的有意义条件解决有关问题;
3、掌握二次根式乘除法运算,熟练掌握二次根式乘除法法则;
4、掌握二次根式加减法运算,熟练掌握二次根式加减法法则;
导入新课
温故知新
1、什么叫做平方根
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根。
2、什么叫算术平方根
一般地,如果一个非负数的平方等于a,那么这个正数叫做a的算术平方根。
问题:如图,正方形ABCD的边长为2,它的对角线AC
的长是多少?
乙同学:
甲同学:
O
讲授新课
知识点一 二次根式的概念及有意义的条件
50米
a米
塔座所形成的这个直角三角形的
斜边长为______________米。
塔座
米
如图示的值表示正方形的面积,则
正方形的边长是
b-3
a叫被开方数
2. a可以是数,也可以是式;
3. 形式上含有二次根号 ;
5. 既可表示开平方运算,也可表示运算的结果.
1. 表示a的算术平方根;
( 双重非负性);
二次根式的特点:
典例精析
⑴
⑵
(3)
(4) .
,
例1:判断下列式中哪些是二次根式.
,
解:(1)、(3)、(4)是二次根式,(2)不是二次根式.
解:由x-2≥0,得
x≥2.
例2 (1)当x取何值时, 在实数范围内有意义
当x≥2时, 在实数范围内有意义.
当x=9时,
A. x>1 B. x>-1 C. x ≥1 D. x ≥-1
A
(2)当x=0,9时,求二次根式 的值.
(3)要使式子 有意义,则x的取值范围是( )
当x=0时,x-2=-2<0,此时二次根式无意义;
要使二次根式在实数范围内有意义,即需满足被开方数≥0,列不等式求解即可.若二次根式处在分母的位置,应同时考虑分母不为零.
归纳
练一练
1.x取何值时,下列二次根式有意义
求二次根式中字母的取值范围的依据:
1.根号内的式子是非负数。
2.若含有分母,则分母不为零.
知识点二 二次根式的双重非负性
思考: 二次根式的实质是表示一个非负数(或式)的算术平方根.对于任意一个二次根式 ,我们知道:
(1)a为被开方数,为保证其有意义,可知a≥0;
(2) 表示一个数或式的算术平方根,可知 ≥0.
二次根式的被开方数非负
二次根式的值非负
二次根式的双重非负性
典例精析
(2)设 ,试求2x+y的值.
例3(1)若 ,求a -b+c的值.
解:
(1)由题意可知a-2=0,b-3=0,c-4=0,解得a=2,b=3,c=4
所以a-b+c=2-3+4=3;
(2)由题意知,1-x≥0,且x-1≥0,联立解得x=1.从而知y=2017,
所以2x+y=2×1+2017=2019.
多个非负数的和为零,则可得每个非负数均为零.初中阶段学过的非负数主要有绝对值、偶次幂及二次根式.
归纳
知识点三 二次根式的性质与化简
问题:观察比较
积的算术平方根的性质
两个非负数的积的算术平方根等于这两个非负数的算术平方根的积
=
=
=
那么 与 是否相等 ?
要点归纳
(a≥0,b≥0)
,
(a≥0, b>0).
商的算术平方根等于算术平方根的商
积的算术平方根等于算术平方根的积
典例精析
例4:化简
解:(1)
(2)
(3)
(1) ;(2) ;(3) .
最简二次根式:
一般地,被开方数不含分母,也不含能开得尽方的因数或因式,这样的二次根式,叫做最简二次根式.
最简二次根式的条件:
①是二次根式;
②被开方数中不含分母;
③被开方数中不含能开得尽方的因数或因式.
练一练
1:化简:
解:
知识点四 二次根式的乘除法运算
根据什么法则化成
还记得吗
(a≥0,b≥0),
(a≥0,b>0).
二次根式的乘法法则和除法法则
典例精析
例5:计算:
练一练
1:计算:
1.试回顾如何计算3a2·2a3= .
还记得单项式乘以单项式的法则吗?
2. 如何计算呢?
6a5
解:
归纳总结
二次根式的乘法扩充法则
第一步:根号外的系数与系数相乘,积为结果的系数;
第二步:根式和根式按公式相乘.
利用它可以进行二次根式的化简.
想一想
知识点五 二次根式的加减运算
(2)x2+2x2+4y= ;
1.(1)3x2+2x2= ;
2.类比合并同类项的方法,想想如何计算:
解:
3. 能不能再进行计算 为什么
答:不能,因为它们都是最简二次根式,被开方数不相同,所以不能合并.
5x2
3x2+4y
合作探究
同样,二次根式也可以进行加减运算,这时,以前学习的实数的运算法则、运算律仍然适用.当然,如果运算结果中出现某些项,它们各自化简后的被开方数相同,那么应当将这些项合并.
典例精析
解: (1)原式=
例5:计算:
(2)原式=
(3)原式=
练一练
解: (1)原式=
1:计算:
(2)原式=
(3)原式=
(4)原式=
归纳总结
二次根式的加减法法则
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
要点提醒
1.加减法的运算步骤:“一化简二判断三合并”.
2.合并的前提条件:只有被开方数相同的最简二次根式才能进行合并.
知识点六 二次根式的化简求值
下列每组二次根式化成最简二次根式,有什么特点?
与
与
几个二次根式化成最简二次根式后,如果它们的被开方式相同,那么,它们是同类二次根式。
说明:(1)必须是最简二次根式
(2)根指数与被开方数相同
(3)与二次根式的系数无关
与
被开方式相同
交流与发现
要用栅栏围成两个相邻的正方形羊圈,它们的面积分别为27平方米和48平方米,栅栏的长度为多少米?
小羊圈
大羊圈
这两个正方形的边分别为 米 米,栅栏的长度为(3 +4 )米
你能把3 +4 进一步化简吗?
几个二次根式化成最简二次根式后,如果它们的被开方式相同,那么,它们是同类二次根式。
说明:(1)必须是最简二次根式
(2)根指数与被开方数相同
(3)与二次根式的系数无关。
化简
,
3
3
3
3
27
2
=
×
=
3
4
3
4
48
2
=
×
=
典例精析
例6:已知 ,求
解析:先化简已知条件,再利用乘法公式变形,即a2+b2=(a+b)2-2ab,最后代入求解.
解:
练一练
1.如果最简二次根式 与 是同类二次根式,求m、n 的值.
解:由题意,得
m+n-2=2
m-n =2
∴ m=3 , n =1
2:计算:
解:
(1)
(2)
解法一:
(3)
你还有其他解法吗?
解法二: 原式=
解: (4)原式=
思考:还可以继续化简吗?为什么?
如果算式当中有个别二次根式化简最简二次根式仍不能与其它最简二次根式合并同类项,结果中可保留,不必化为最简式.
提醒
知识点七 二次根式的加减运算
例7:教师节就要到了,李欣同学准备做两张大小不同的正方形贺卡送给老师以表示祝贺,其中一张面积为288平方厘米,另一张面积为338平方厘米.如果用彩带把贺卡镶边会更漂亮,她现在有1.5米的彩带,请你帮忙算一算她的彩带够不够用.
解析:可以通过两个正方形的面积分别计算出正方形的边长,进一步求出两个正方形的周长之和,与1.5米比较即可得出结论.
解:贺卡的周长为
答:李欣的彩带够用.
练一练
1.在一个边长为 cm的正方形内部,挖去一个边长为 cm的正方形,求剩余部分的面积.
解:由题意得,
即剩余部分的面积是
当堂练习
课堂小结
(1)二次根式的性质
(2)最简二次根式的定义
(3)二次根式值的化简
二次根式的乘法法则和除法法则:
算术平方根的积等于各个被开方数积的算术平方根
两个二次根式相除,将它们的被开方数相除的商作为商的被开方数
同类二次根式:
(1)必须是最简二次根式
(2)根指数与被开方数相同
(3)与二次根式的系数无关
二次根式的加减实质是合并同类二次根式
法则:同类二次根式的系数相加减,做为结果的系数,根号及被开方术都不变
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
