12.1.1同底数幂的乘法 课件(19张PPT)
文档属性
| 名称 | 12.1.1同底数幂的乘法 课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 20:43:17 | ||
图片预览






文档简介
(共19张PPT)
12.1.1同底数幂的乘法
华师大版 八年级上册
教学目标
1.掌握同底数幂的乘法法则,并能运用它进行熟练的计算.
2.能利用同底数幂的乘法法则解决简单实际的问题.
【教学重点】同底数幂乘法法则的推导与运用.
【教学难点】同底数幂乘法法则的运用.
新知导入
我们来看下面的问题吧
2009年10月29日,我国国防科技大学成功研制 的“天河一号”其运算速度每秒可达1015次运算,那么它工作103秒可进行多少次运算
1015×103
= ?
新知探究
根据乘方的意义,计算下列各式:
(1)23×24 (2)53×54 (3)a3×a4.
=(2×2×2)×(2×2×2×2)
=2×2×2×2×2×2×2
=27
23 × 24
(1)
(根据 。)
(根据 。)
(根据 。)
乘法结合律
幂的意义
幂的意义
=23+4
新知探究
(2)53×54=
(5×5×5)×(5×5×5×5)
=5×5×5×5×5×5×5
=57
=3+4
3
4
3个5
4个5
7个5
(3)a3·a4=
(a · a · a)(a · a · a · a)
=a · a · a · a · a · a · a
=a7
=3+4
3
4
3个a
4个a
7个a
新知探究
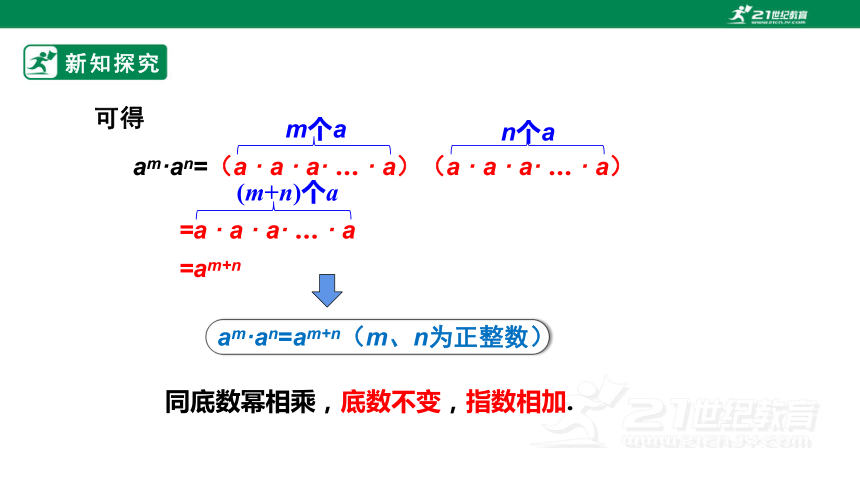
am·an=(a · a · a· … · a)(a · a · a· … · a)
=a · a · a· … · a
=am+n
am·an=am+n(m、n为正整数)
同底数幂相乘,底数不变,指数相加.
可得
m个a
n个a
(m+n)个a
例题讲解
例1 计算
(1)103x104
(2)a·a3
(3)a·a3·a5
解:
(1)103x104=103+4=107
(2)a·a3=a1+3=a4
(3)a·a3·a5=a1+3+5=a9
拓展:am·an·ap=am+n+p
巩固练习
1、计算a2 a的结果是( )
易错点:当指数为1时,可以不写,但不能认为没有指数.
B
巩固练习
2、下列结果等于a6的是( )
D
易错点:注意公式的灵活选用
新知讲解
例2、(转化思想)计算:(x-y)2 (y-x)3
互为相反数
解题策略:当底数为多项式,且互为相反数时,时常用下面的公式转化为同底数幂相乘:
典例讲解
例3、如果xm-n·x2n+1=x11,且ym-1·y4-n=y5,求m、n的值.
解:根据同底数幂的乘法法则得:
(m-n)+(2n+1)=11
(m-1)+(4-n)=5
解得 m=6,n=4
典例讲解
例4、若2x=16,2y=8则2x+y+2=_______
312
思路分析:
解题策略:逆用同底数幂的乘法法则,将2x+y+2转化为同底数幂相乘,再将数值代入计算即可得到结果。
课堂小结
同底数幂相乘,底数不变,指数相加.
am·an=am+n(m、n为正整数)
同底数幂的乘法
当堂检测
1.判断下列计算是否正确,并说明理由:
(1)a·a2=a2
(2)a+a2=a3
(3)a3·a3=a9
(4)a3+a3=a6
×
a·a2=a2+1=a3
×
×
a3·a3=a3+3=a6
×
a3+a3=2a3
当堂检测
2.计算:
(1)102×105
(2)a3·a7
(3)x·x5·x7
=107
=a10
=x13
当堂检测
3.已知x xm xn=x14(x≠1),且m比n大3,求mn的值
当堂检测
4.已知ax=5,ax+y=25,求ax+ay的值
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
12.1.1同底数幂的乘法
华师大版 八年级上册
教学目标
1.掌握同底数幂的乘法法则,并能运用它进行熟练的计算.
2.能利用同底数幂的乘法法则解决简单实际的问题.
【教学重点】同底数幂乘法法则的推导与运用.
【教学难点】同底数幂乘法法则的运用.
新知导入
我们来看下面的问题吧
2009年10月29日,我国国防科技大学成功研制 的“天河一号”其运算速度每秒可达1015次运算,那么它工作103秒可进行多少次运算
1015×103
= ?
新知探究
根据乘方的意义,计算下列各式:
(1)23×24 (2)53×54 (3)a3×a4.
=(2×2×2)×(2×2×2×2)
=2×2×2×2×2×2×2
=27
23 × 24
(1)
(根据 。)
(根据 。)
(根据 。)
乘法结合律
幂的意义
幂的意义
=23+4
新知探究
(2)53×54=
(5×5×5)×(5×5×5×5)
=5×5×5×5×5×5×5
=57
=3+4
3
4
3个5
4个5
7个5
(3)a3·a4=
(a · a · a)(a · a · a · a)
=a · a · a · a · a · a · a
=a7
=3+4
3
4
3个a
4个a
7个a
新知探究
am·an=(a · a · a· … · a)(a · a · a· … · a)
=a · a · a· … · a
=am+n
am·an=am+n(m、n为正整数)
同底数幂相乘,底数不变,指数相加.
可得
m个a
n个a
(m+n)个a
例题讲解
例1 计算
(1)103x104
(2)a·a3
(3)a·a3·a5
解:
(1)103x104=103+4=107
(2)a·a3=a1+3=a4
(3)a·a3·a5=a1+3+5=a9
拓展:am·an·ap=am+n+p
巩固练习
1、计算a2 a的结果是( )
易错点:当指数为1时,可以不写,但不能认为没有指数.
B
巩固练习
2、下列结果等于a6的是( )
D
易错点:注意公式的灵活选用
新知讲解
例2、(转化思想)计算:(x-y)2 (y-x)3
互为相反数
解题策略:当底数为多项式,且互为相反数时,时常用下面的公式转化为同底数幂相乘:
典例讲解
例3、如果xm-n·x2n+1=x11,且ym-1·y4-n=y5,求m、n的值.
解:根据同底数幂的乘法法则得:
(m-n)+(2n+1)=11
(m-1)+(4-n)=5
解得 m=6,n=4
典例讲解
例4、若2x=16,2y=8则2x+y+2=_______
312
思路分析:
解题策略:逆用同底数幂的乘法法则,将2x+y+2转化为同底数幂相乘,再将数值代入计算即可得到结果。
课堂小结
同底数幂相乘,底数不变,指数相加.
am·an=am+n(m、n为正整数)
同底数幂的乘法
当堂检测
1.判断下列计算是否正确,并说明理由:
(1)a·a2=a2
(2)a+a2=a3
(3)a3·a3=a9
(4)a3+a3=a6
×
a·a2=a2+1=a3
×
×
a3·a3=a3+3=a6
×
a3+a3=2a3
当堂检测
2.计算:
(1)102×105
(2)a3·a7
(3)x·x5·x7
=107
=a10
=x13
当堂检测
3.已知x xm xn=x14(x≠1),且m比n大3,求mn的值
当堂检测
4.已知ax=5,ax+y=25,求ax+ay的值
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
