2022—2023学年人教版数学八年级上册11.1.1三角形的边课件(共18张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.1.1三角形的边课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 16:52:42 | ||
图片预览

文档简介
(共18张PPT)
11.1.1 三角形的边
一、导入新课
仔细观察图片上出现最多的图形是什么?
水分子结构示意图
飞机机翼
埃及金字塔
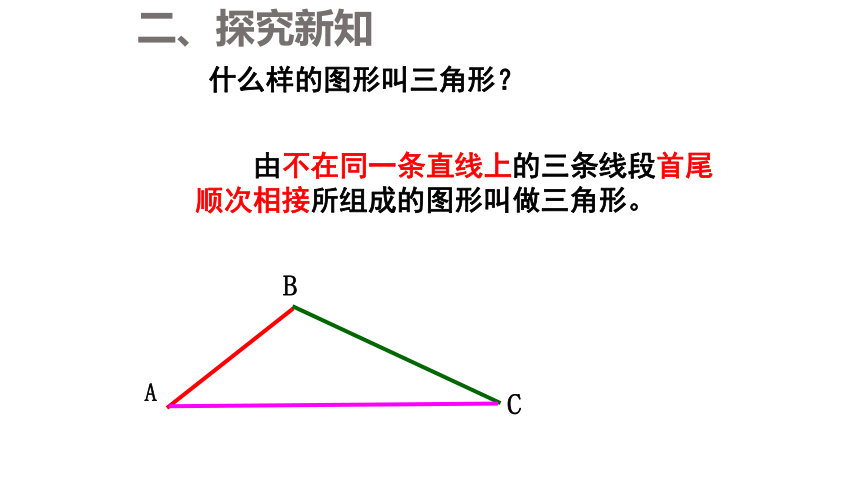
什么样的图形叫三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
A
B
C
二、探究新知
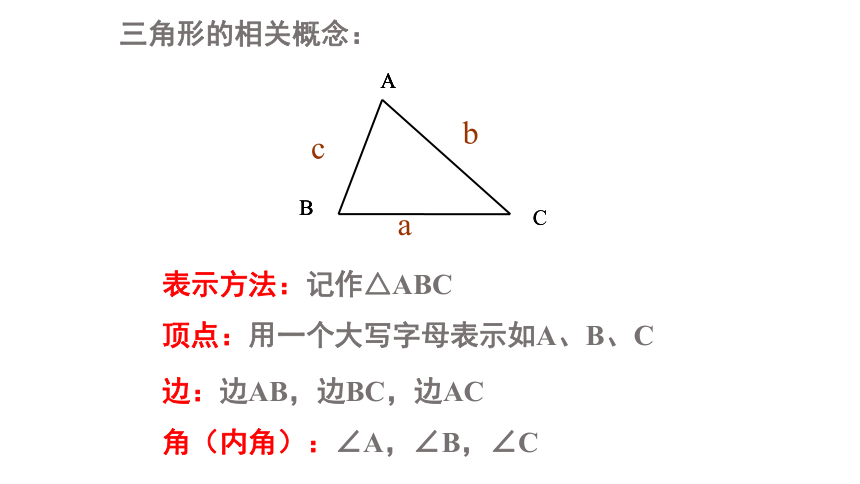
顶点:用一个大写字母表示如A、B、C
边:边AB,边BC,边AC
角(内角):∠A,∠B,∠C
表示方法:记作△ABC
A
B
C
三角形的相关概念:
a
c
b
A
B
A
C
B
A
夯实基础
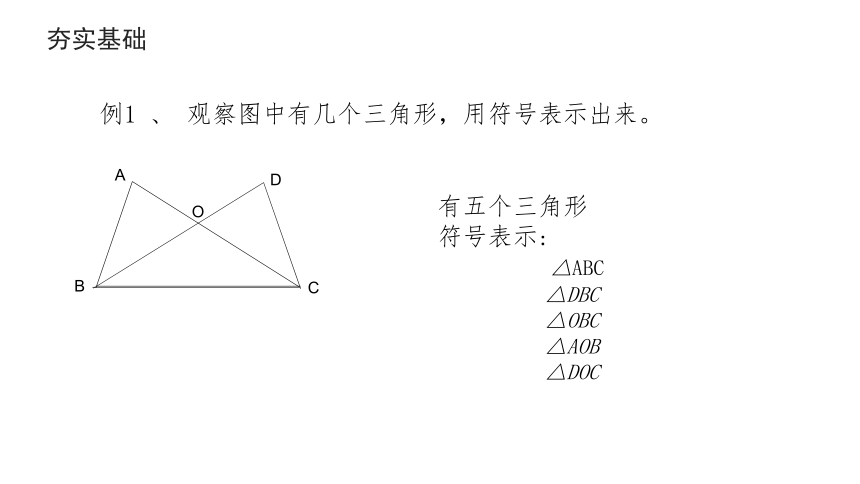
例1 、 观察图中有几个三角形,用符号表示出来。
A
D
O
B
C
有五个三角形
符号表示:
△ABC
△DBC
△OBC
△AOB
△DOC
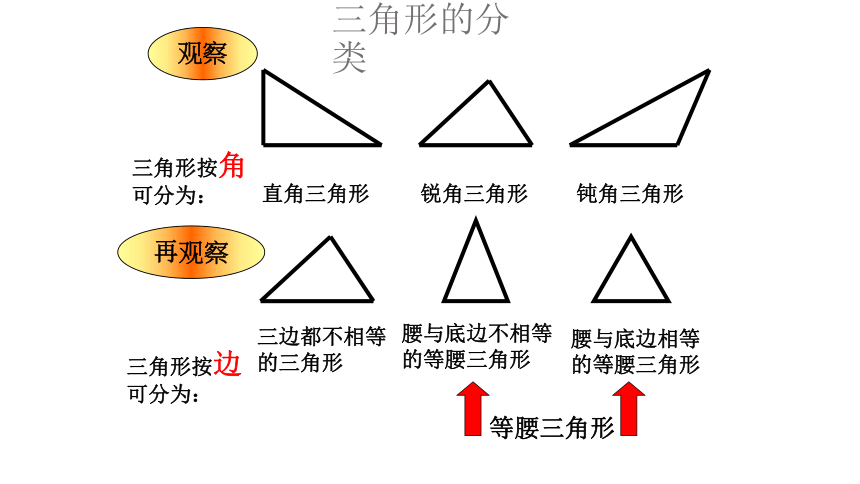
观察
三角形按角
可分为:
直角三角形
锐角三角形
钝角三角形
三角形按边
可分为:
三边都不相等
的三角形
腰与底边不相等
的等腰三角形
腰与底边相等
的等腰三角形
再观察
等腰三角形
三角形的分类
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
三角形的分类
等腰三角形
腰≠底的三角形
等边三角形
不等边三角形
等腰三角形
等边三角形
例2 、 观察图形,回答问题。
研究例题,创新知识
A
B
C
判断
AB+AC BC
BC+AB AC
BC+AC AB
两点之间,
线段最短
三角形的任意两边
之和大于第三边
>
>
>
三角形两边的和大于第三边
三角形两边的差小于第三边
夯实基础
例3 、判断下列长度的三条线段能否拼成三角形?
(1)3cm、8cm、4cm; (2)2cm、6cm、5cm;
(3)5cm、6cm、10cm;(4)3cm、5cm、8cm;
否
能
能
否
小窍门:用较短的两条线段之和与最长的线段比较,若大,能组成三角形,反之,则不能。
自主画图,思考归纳
学生活动:在一个三角形中,任何两边之差与第三边有什么关系?画一个三角形,量出三边长度,探究上述问题,得出结论。
归纳:(1)三角形三边关系:两边之和大于第三边及两边之差小于第三边.
(2)在做题时,不仅要考虑到两边之和大于第三边,还要考虑到两边之差小于第三边。
夯实基础
例4 、 若三角形的两边长分别是2和7,求第三边长的范围;当第三边长为奇数,求第三边的长。
归纳:设x为三角形第三条边的长,则有两边之差解:设第三边长为x,则应有
即5x>7-2
x<7+2
因为第三边长为奇数,所以第三边长取7
巩固练习1有三根木棒长分别为3cm、6cm和2cm,用这木棒能否围成一个三角形 2
用一条长为18cm的细绳围成一个等腰三角形
1、腰长是底边长的2倍,各边长是多少?
2、围成一边长是5cm的等腰三角形的边长
3、围成一边长是4cm的等腰三角形的边长
巩固练习
1.等腰三角形是等边三角形。( )
2.等边三角形是特殊的等腰三角形。( )
3.三角形按边分分为等腰三角形、等边三角形、
不等边三角形。( )
4.已知等腰三角形的周长为16,且底边长为3,
则腰长是_____。
√
×
×
6.5
5.下列三条线段,能构成三角形的是( )
A.1cm,2cm,3cm B.2cm,3cm,4cm
C.6cm,8cm,15cm D.12cm,3cm,8cm
6.已知等腰三角形的两边长分别为8cm,3cm,则这个三角形的周长为( )
A.14cm B.19cm
C.14cm或19cm D.不确定
B
B
小结
三角形
定义及其基本要素
顶点、角、边、表示方法
分类
按角分类
按边分类
三边关系
原理
两点之间线段最短
内容
两边之和大于第三边
两边之差小于第三边
a-bb,x为第三边)
应用
11.1.1 三角形的边
一、导入新课
仔细观察图片上出现最多的图形是什么?
水分子结构示意图
飞机机翼
埃及金字塔
什么样的图形叫三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
A
B
C
二、探究新知
顶点:用一个大写字母表示如A、B、C
边:边AB,边BC,边AC
角(内角):∠A,∠B,∠C
表示方法:记作△ABC
A
B
C
三角形的相关概念:
a
c
b
A
B
A
C
B
A
夯实基础
例1 、 观察图中有几个三角形,用符号表示出来。
A
D
O
B
C
有五个三角形
符号表示:
△ABC
△DBC
△OBC
△AOB
△DOC
观察
三角形按角
可分为:
直角三角形
锐角三角形
钝角三角形
三角形按边
可分为:
三边都不相等
的三角形
腰与底边不相等
的等腰三角形
腰与底边相等
的等腰三角形
再观察
等腰三角形
三角形的分类
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
三角形的分类
等腰三角形
腰≠底的三角形
等边三角形
不等边三角形
等腰三角形
等边三角形
例2 、 观察图形,回答问题。
研究例题,创新知识
A
B
C
判断
AB+AC BC
BC+AB AC
BC+AC AB
两点之间,
线段最短
三角形的任意两边
之和大于第三边
>
>
>
三角形两边的和大于第三边
三角形两边的差小于第三边
夯实基础
例3 、判断下列长度的三条线段能否拼成三角形?
(1)3cm、8cm、4cm; (2)2cm、6cm、5cm;
(3)5cm、6cm、10cm;(4)3cm、5cm、8cm;
否
能
能
否
小窍门:用较短的两条线段之和与最长的线段比较,若大,能组成三角形,反之,则不能。
自主画图,思考归纳
学生活动:在一个三角形中,任何两边之差与第三边有什么关系?画一个三角形,量出三边长度,探究上述问题,得出结论。
归纳:(1)三角形三边关系:两边之和大于第三边及两边之差小于第三边.
(2)在做题时,不仅要考虑到两边之和大于第三边,还要考虑到两边之差小于第三边。
夯实基础
例4 、 若三角形的两边长分别是2和7,求第三边长的范围;当第三边长为奇数,求第三边的长。
归纳:设x为三角形第三条边的长,则有两边之差
即5
x<7+2
因为第三边长为奇数,所以第三边长取7
巩固练习1有三根木棒长分别为3cm、6cm和2cm,用这木棒能否围成一个三角形 2
用一条长为18cm的细绳围成一个等腰三角形
1、腰长是底边长的2倍,各边长是多少?
2、围成一边长是5cm的等腰三角形的边长
3、围成一边长是4cm的等腰三角形的边长
巩固练习
1.等腰三角形是等边三角形。( )
2.等边三角形是特殊的等腰三角形。( )
3.三角形按边分分为等腰三角形、等边三角形、
不等边三角形。( )
4.已知等腰三角形的周长为16,且底边长为3,
则腰长是_____。
√
×
×
6.5
5.下列三条线段,能构成三角形的是( )
A.1cm,2cm,3cm B.2cm,3cm,4cm
C.6cm,8cm,15cm D.12cm,3cm,8cm
6.已知等腰三角形的两边长分别为8cm,3cm,则这个三角形的周长为( )
A.14cm B.19cm
C.14cm或19cm D.不确定
B
B
小结
三角形
定义及其基本要素
顶点、角、边、表示方法
分类
按角分类
按边分类
三边关系
原理
两点之间线段最短
内容
两边之和大于第三边
两边之差小于第三边
a-b
应用
