人教版八年级上册11.2.2三角形的外角课件 (共19页PPT)
文档属性
| 名称 | 人教版八年级上册11.2.2三角形的外角课件 (共19页PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 16:57:50 | ||
图片预览





文档简介
(共19张PPT)
11.2.2 三角形的外角
2、在ABC中,
(1)∠C=90°,∠A=20 ° ,则∠B= ;
(2)∠A=40 ° ,∠B=∠C,则∠B= .
1、三角形三个内角的和等于多少度?
知识回顾
3、在△ABC中,
∠A:∠B:∠C=2:3:4则∠A= ,
∠B= ∠C=
40°
60°
80°
70°
70°
三角形的内角和等于180度
情景引入
B
C
A
1
3
.
2
M
探索新知
B
C
A
1
2
3
操作:画出一个三角形的所有外角,并用数字标出来。
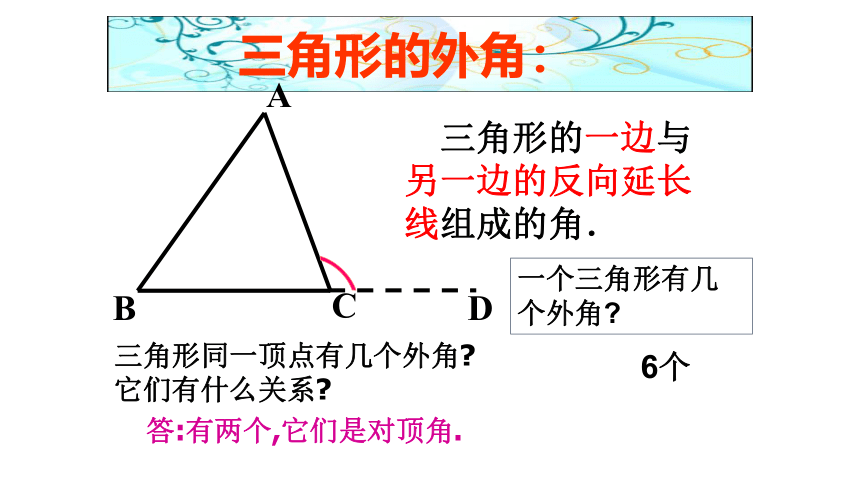
三角形的一边与另一边的延长线组成的角,叫做三角形的外角。
三角形外角的定义:
A
B
C
D
三角形的外角:
三角形的一边与另一边的反向延长线组成的角.
一个三角形有几个外角
6个
三角形同一顶点有几个外角
它们有什么关系
答:有两个,它们是对顶角.
A
B
C
D
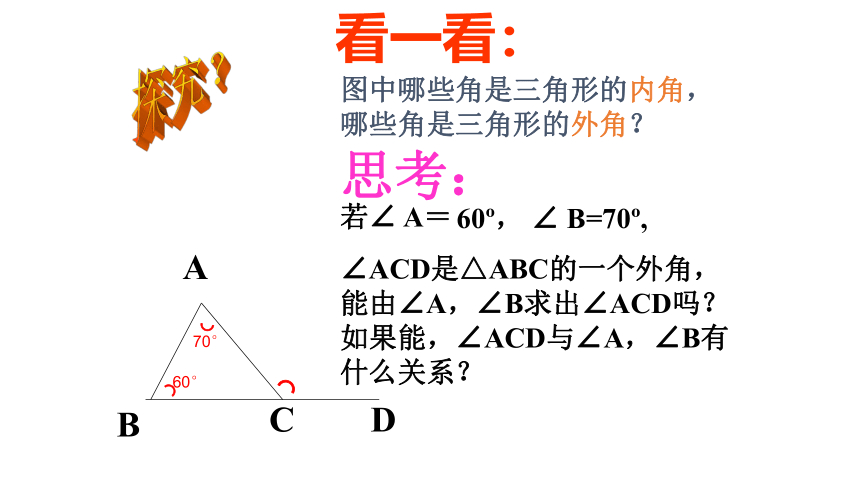
看一看:
思考:
若∠ A=
60 , ∠ B=70 ,
∠ACD是△ABC的一个外角,能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有 什么关系?
探究?
图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒
⌒
⌒
60°
70°
通过上题的计算,任意一个三角形的外角与他不相邻的两个内角是否都有这种关系?请你试着用自己的语言说一说.
想一想:
三角形的一个外角等于与它不相邻的两个内角的和。
结论:
三角形外角性质
D
解:过C作CE平行于AB
A
B
C
1
2
∴ ∠1= ∠B
(两直线平行,同位角相等)
∠2= ∠A
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B
E
三角形的一个外角等于与它不相邻的两个内角的和
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
D
A
C
B
>
>
你选谁 ?
∠1=40 °, ∠2=140 °
∠1=18 °, ∠2=130 °
练习:说出下列图形中∠1和∠2的度数:
尝试应用
A
B
C
1
A
B
C
练习:说出下列图形中∠1和∠2的度数:
尝试应用
A
C
B
D
探究:
三角形的外角和
现在回到我们最初提出的问题.
在一个三角形花坛的外围走一圈,在每一个拐弯的地方
都转了一个角度(∠1,∠2,∠3),那么回到原来位
置时(方向与出发时相同),一共转了多少度?
通过我们这节课学习的三角形外
角的定义以及性质,我们现在来
解决这个问题,首先,我们将实
际问题转化成数学问题.
如图, ∠ BAE, ∠ CBF, ∠ ACD 是△ABC的三个外角,它们的和是多少?
由三角形的一个外角等于与它不相邻的
两个内角的和,得
∠ BAE= ∠ 2+ ∠ 3,
∠ cbf= ∠ 1+ ∠ 3,
∠ ACD= ∠ 1+ ∠ 2.
所以∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3).
说出下列图形中∠ 1和∠ 2的度数:
由∠1+∠2+∠3=180°,得
∠BAE+∠CBF+∠ACD=2×180°=360°.
例2
解:
你还有其他解法吗?
尝试应用
B
C
A
1
2
3
6
5
4
尝试应用
∴∠1=∠5+∠6
同理,∠2=∠4+∠6
∠3=∠4+∠5
∴∠1+∠2+∠3=2(∠4+∠5+∠6)
∵∠4+∠5+∠6=180°
∴∠1+∠2+∠3=2×180°=360°
结论:三角形的外角和等于360°
B
C
A
1
2
3
6
5
4
1、三角形外角的两条性质
① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是3600
归纳:
如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
40
40
⌒
练习:
1、如图(甲),在五角星图形中,求∠A+∠B+∠C+∠D+∠E的度数。
2、把图(乙)、(丙)叫蜕化的五角星,问:它们的五角之和与五角星图形的五角之和仍相等吗?为什么?
C
D
A
B
C
D
E
B
A
C
D
E
A
B
E
(甲)
(乙)
(丙)
能力提升:
11.2.2 三角形的外角
2、在ABC中,
(1)∠C=90°,∠A=20 ° ,则∠B= ;
(2)∠A=40 ° ,∠B=∠C,则∠B= .
1、三角形三个内角的和等于多少度?
知识回顾
3、在△ABC中,
∠A:∠B:∠C=2:3:4则∠A= ,
∠B= ∠C=
40°
60°
80°
70°
70°
三角形的内角和等于180度
情景引入
B
C
A
1
3
.
2
M
探索新知
B
C
A
1
2
3
操作:画出一个三角形的所有外角,并用数字标出来。
三角形的一边与另一边的延长线组成的角,叫做三角形的外角。
三角形外角的定义:
A
B
C
D
三角形的外角:
三角形的一边与另一边的反向延长线组成的角.
一个三角形有几个外角
6个
三角形同一顶点有几个外角
它们有什么关系
答:有两个,它们是对顶角.
A
B
C
D
看一看:
思考:
若∠ A=
60 , ∠ B=70 ,
∠ACD是△ABC的一个外角,能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有 什么关系?
探究?
图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒
⌒
⌒
60°
70°
通过上题的计算,任意一个三角形的外角与他不相邻的两个内角是否都有这种关系?请你试着用自己的语言说一说.
想一想:
三角形的一个外角等于与它不相邻的两个内角的和。
结论:
三角形外角性质
D
解:过C作CE平行于AB
A
B
C
1
2
∴ ∠1= ∠B
(两直线平行,同位角相等)
∠2= ∠A
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B
E
三角形的一个外角等于与它不相邻的两个内角的和
∠ACD ∠A (<、>);
∠ACD ∠B (<、>)
D
A
C
B
>
>
你选谁 ?
∠1=40 °, ∠2=140 °
∠1=18 °, ∠2=130 °
练习:说出下列图形中∠1和∠2的度数:
尝试应用
A
B
C
1
A
B
C
练习:说出下列图形中∠1和∠2的度数:
尝试应用
A
C
B
D
探究:
三角形的外角和
现在回到我们最初提出的问题.
在一个三角形花坛的外围走一圈,在每一个拐弯的地方
都转了一个角度(∠1,∠2,∠3),那么回到原来位
置时(方向与出发时相同),一共转了多少度?
通过我们这节课学习的三角形外
角的定义以及性质,我们现在来
解决这个问题,首先,我们将实
际问题转化成数学问题.
如图, ∠ BAE, ∠ CBF, ∠ ACD 是△ABC的三个外角,它们的和是多少?
由三角形的一个外角等于与它不相邻的
两个内角的和,得
∠ BAE= ∠ 2+ ∠ 3,
∠ cbf= ∠ 1+ ∠ 3,
∠ ACD= ∠ 1+ ∠ 2.
所以∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3).
说出下列图形中∠ 1和∠ 2的度数:
由∠1+∠2+∠3=180°,得
∠BAE+∠CBF+∠ACD=2×180°=360°.
例2
解:
你还有其他解法吗?
尝试应用
B
C
A
1
2
3
6
5
4
尝试应用
∴∠1=∠5+∠6
同理,∠2=∠4+∠6
∠3=∠4+∠5
∴∠1+∠2+∠3=2(∠4+∠5+∠6)
∵∠4+∠5+∠6=180°
∴∠1+∠2+∠3=2×180°=360°
结论:三角形的外角和等于360°
B
C
A
1
2
3
6
5
4
1、三角形外角的两条性质
① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是3600
归纳:
如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
80°
70°
40
40
⌒
练习:
1、如图(甲),在五角星图形中,求∠A+∠B+∠C+∠D+∠E的度数。
2、把图(乙)、(丙)叫蜕化的五角星,问:它们的五角之和与五角星图形的五角之和仍相等吗?为什么?
C
D
A
B
C
D
E
B
A
C
D
E
A
B
E
(甲)
(乙)
(丙)
能力提升:
