人教版八年级上册13.1.2线段的垂直平分线的性质 课件(共20张PPT)
文档属性
| 名称 | 人教版八年级上册13.1.2线段的垂直平分线的性质 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 17:05:39 | ||
图片预览



文档简介
(共20张PPT)
13.1.2线段的垂直平分线的性质
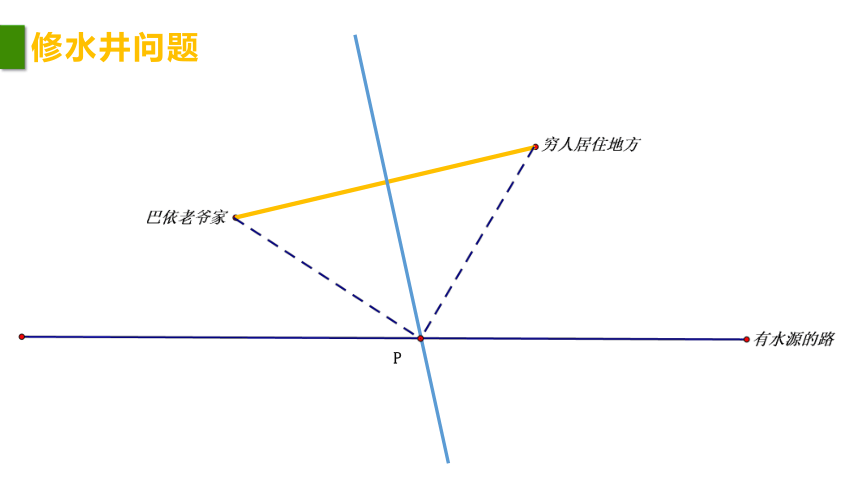
背景:村庄里用水不便,阿凡提提出修一口水井,巴依老爷和穷人居住的地方都没有水源,只有一条路边有水源
我和穷人对半出钱,但是水井要修在我家对面
不行,要修在离我们穷人近一些的地方
找一点到巴依老爷和穷人距离相等的地方,怎么找?
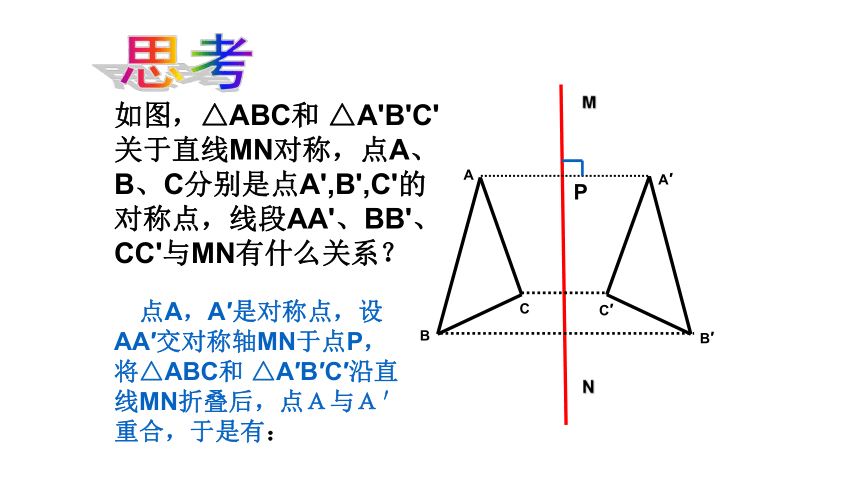
思考
M
N
A
B
C
A′
C′
B′
如图,△ABC和 △A'B'C'关于直线MN对称,点A、B、C分别是点A',B',C'的对称点,线段AA'、BB'、CC'与MN有什么关系?
P
点A,A′是对称点,设AA′交对称轴MN于点P,将△ABC和 △A′B′C′沿直线MN折叠后,点A与A′重合,于是有:
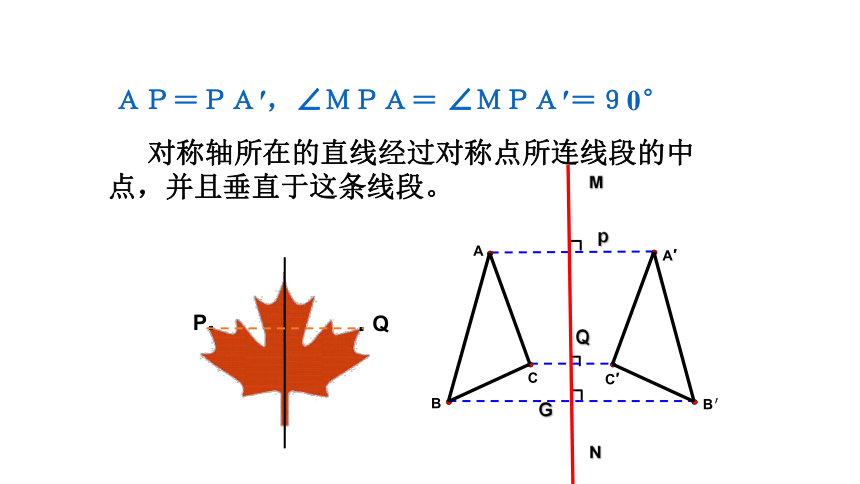
AP=PA′,∠MPA= ∠MPA′=90°
对称轴所在的直线经过对称点所连线段的中点,并且垂直于这条线段。
M
N
Q
p
G
A
B
C
A′
C′
B′
P.
. Q
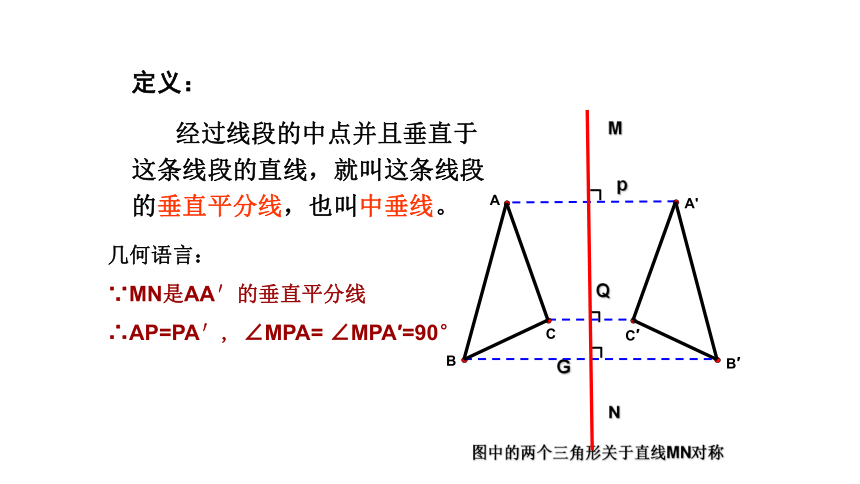
定义:
经过线段的中点并且垂直于这条线段的直线,就叫这条线段的垂直平分线,也叫中垂线。
图中的两个三角形关于直线MN对称
Q
p
G
M
N
A
B
C
A'
C′
B′
几何语言:
∵MN是AA′的垂直平分线
∴AP=PA′, ∠MPA= ∠MPA′=90°
轴对称的性质:
如果两个图形关于某条直线对称,那么对称轴是任何一对对称点所连线段的垂直平分线。
即对称点的连线被对称轴垂直平分。
类似地,轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线。
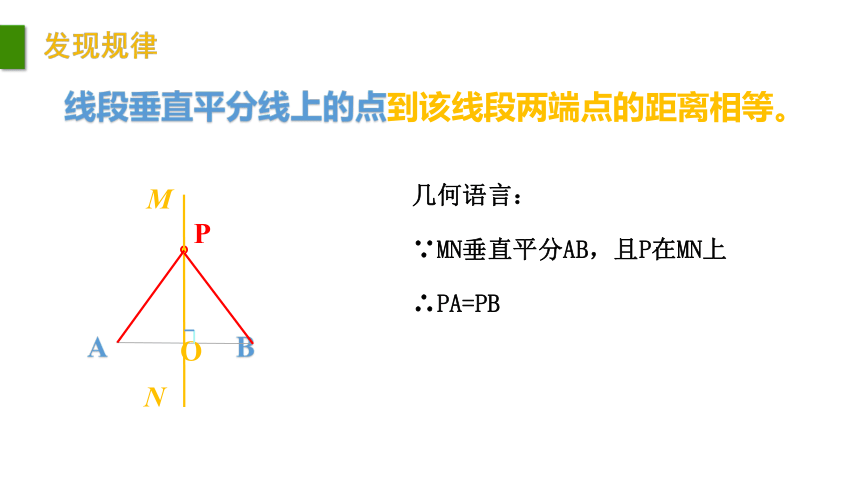
发现规律
线段垂直平分线上的点到该线段两端点的距离相等。
几何语言:
∵MN垂直平分AB,且P在MN上
∴PA=PB
P
A B
M
O
N
修水井问题
P
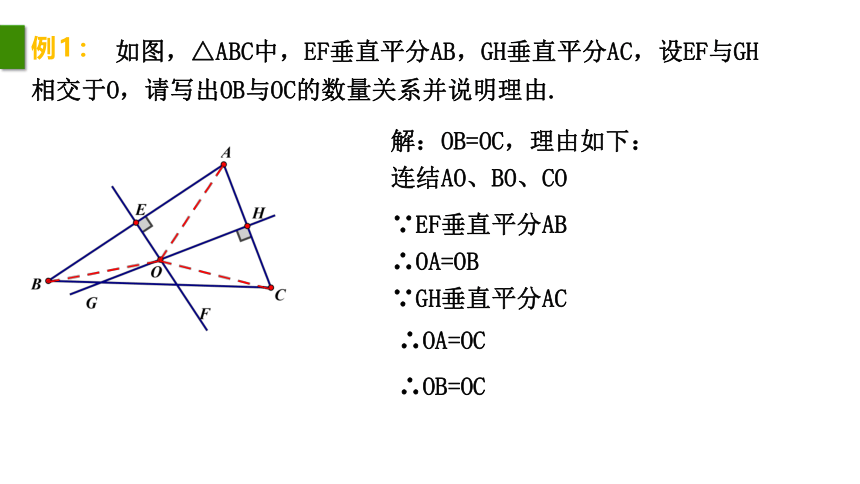
例1:
如图,△ABC中,EF垂直平分AB,GH垂直平分AC,设EF与GH
相交于O,请写出OB与OC的数量关系并说明理由.
连结AO、BO、CO
∵EF垂直平分AB
∴OA=OB
∵GH垂直平分AC
∴OA=OC
解:OB=OC,理由如下:
∴OB=OC
例2 已知:如图,ΔABC中,边AB,BC的垂直平分线交于点P.
求证:(1)PA=PB=PC;
(2)点P在边AC的垂直平分线上
B
A
C
D
E
F
G
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
分析:
已知:如图,ΔABC中,边AB,BC的垂直平分线交于点P.
求证:(1)PA=PB=PC;
(2)点P在边AC的垂直平分线上
A
F
D
P
B
G
E
C
证明:(1)∵DE是AB的垂直平分线
∴PA=PB
∵FG是BC的垂直平分线
∴PB=PC
∴PA=PB=PC
(2)由(1)知PA=PC
∴点P在边AC的垂直平分线上
小试牛刀
1.下列说法错误的是( )。
A.D.E 是线段 AB 的垂直平分线上的两点,则 AD=BD,AE=BE 。B.若 AD=BD,AE=BE,则线段 DE 所在直线是线段 AB 的垂直平分线 。
C.若 PA=PB,则点 P 在线段 AB 的垂直平分线上 。
D.若 PA=PB,则过点 P 的直线是线段 AB 的垂直平分线 。
D
2.如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,△BCD的周长是
C
B
E
A
D
19
变式一:如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上
(1)AB,AC,CE 的长度有什么关系?
(2)AB+BD与DE 有什么关系?
解:(1) AB=AC=CE,理由如下:
∵AD⊥BC,BD =DC ,
∴AB =AC;
又∵点C 在AE 的垂直平分线上,
∴AC=CE,
∴AB=AC=CE。
(2) AB +BD =DE,理由如下:
∵AB =CE,BD =DC,
∴AB +BD =CD +CE,
即AB +BD =DE
A
B
C
D
E
变式二:易错题:
如图,直线l是线段AB的垂直平分线,直线L与线段AB相交于点O,P为L上一点,C,D为线段AB上的两点,有下列结论:①PA=PB;②PC=PD;③AO=BO;④∠AOP=90°.其中一定正确的结论有:
①③④
练习1:作出下列图形的一条对称轴,和同学比较一下,你们作出的对称轴一样吗?
课堂练习
课堂练习
练习2:如图,角是轴对称图形吗?如果是,它的对称轴是什么?
角是轴对称图形,角平分线所在的直线就是角的对称轴.
课堂练习
练习3:如图,与图形A成轴对称的是哪个图形?画出它们的对称轴.
课后思考
练习4:如图,在Rt△ABC中,∠C=90°,AD是角平分线且AD=BD,AC=10. 求AB的长度.
提示:过点D作DE⊥AB于E
A
B
C
D
E
天生我才
三、小结
线段垂直平分线的性质:线段垂直平分线上的点到这条线段两个端点的距离相等。
线段垂直平分线的判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
谈谈你这节课的收获
13.1.2线段的垂直平分线的性质
背景:村庄里用水不便,阿凡提提出修一口水井,巴依老爷和穷人居住的地方都没有水源,只有一条路边有水源
我和穷人对半出钱,但是水井要修在我家对面
不行,要修在离我们穷人近一些的地方
找一点到巴依老爷和穷人距离相等的地方,怎么找?
思考
M
N
A
B
C
A′
C′
B′
如图,△ABC和 △A'B'C'关于直线MN对称,点A、B、C分别是点A',B',C'的对称点,线段AA'、BB'、CC'与MN有什么关系?
P
点A,A′是对称点,设AA′交对称轴MN于点P,将△ABC和 △A′B′C′沿直线MN折叠后,点A与A′重合,于是有:
AP=PA′,∠MPA= ∠MPA′=90°
对称轴所在的直线经过对称点所连线段的中点,并且垂直于这条线段。
M
N
Q
p
G
A
B
C
A′
C′
B′
P.
. Q
定义:
经过线段的中点并且垂直于这条线段的直线,就叫这条线段的垂直平分线,也叫中垂线。
图中的两个三角形关于直线MN对称
Q
p
G
M
N
A
B
C
A'
C′
B′
几何语言:
∵MN是AA′的垂直平分线
∴AP=PA′, ∠MPA= ∠MPA′=90°
轴对称的性质:
如果两个图形关于某条直线对称,那么对称轴是任何一对对称点所连线段的垂直平分线。
即对称点的连线被对称轴垂直平分。
类似地,轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线。
发现规律
线段垂直平分线上的点到该线段两端点的距离相等。
几何语言:
∵MN垂直平分AB,且P在MN上
∴PA=PB
P
A B
M
O
N
修水井问题
P
例1:
如图,△ABC中,EF垂直平分AB,GH垂直平分AC,设EF与GH
相交于O,请写出OB与OC的数量关系并说明理由.
连结AO、BO、CO
∵EF垂直平分AB
∴OA=OB
∵GH垂直平分AC
∴OA=OC
解:OB=OC,理由如下:
∴OB=OC
例2 已知:如图,ΔABC中,边AB,BC的垂直平分线交于点P.
求证:(1)PA=PB=PC;
(2)点P在边AC的垂直平分线上
B
A
C
D
E
F
G
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
分析:
已知:如图,ΔABC中,边AB,BC的垂直平分线交于点P.
求证:(1)PA=PB=PC;
(2)点P在边AC的垂直平分线上
A
F
D
P
B
G
E
C
证明:(1)∵DE是AB的垂直平分线
∴PA=PB
∵FG是BC的垂直平分线
∴PB=PC
∴PA=PB=PC
(2)由(1)知PA=PC
∴点P在边AC的垂直平分线上
小试牛刀
1.下列说法错误的是( )。
A.D.E 是线段 AB 的垂直平分线上的两点,则 AD=BD,AE=BE 。B.若 AD=BD,AE=BE,则线段 DE 所在直线是线段 AB 的垂直平分线 。
C.若 PA=PB,则点 P 在线段 AB 的垂直平分线上 。
D.若 PA=PB,则过点 P 的直线是线段 AB 的垂直平分线 。
D
2.如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,△BCD的周长是
C
B
E
A
D
19
变式一:如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上
(1)AB,AC,CE 的长度有什么关系?
(2)AB+BD与DE 有什么关系?
解:(1) AB=AC=CE,理由如下:
∵AD⊥BC,BD =DC ,
∴AB =AC;
又∵点C 在AE 的垂直平分线上,
∴AC=CE,
∴AB=AC=CE。
(2) AB +BD =DE,理由如下:
∵AB =CE,BD =DC,
∴AB +BD =CD +CE,
即AB +BD =DE
A
B
C
D
E
变式二:易错题:
如图,直线l是线段AB的垂直平分线,直线L与线段AB相交于点O,P为L上一点,C,D为线段AB上的两点,有下列结论:①PA=PB;②PC=PD;③AO=BO;④∠AOP=90°.其中一定正确的结论有:
①③④
练习1:作出下列图形的一条对称轴,和同学比较一下,你们作出的对称轴一样吗?
课堂练习
课堂练习
练习2:如图,角是轴对称图形吗?如果是,它的对称轴是什么?
角是轴对称图形,角平分线所在的直线就是角的对称轴.
课堂练习
练习3:如图,与图形A成轴对称的是哪个图形?画出它们的对称轴.
课后思考
练习4:如图,在Rt△ABC中,∠C=90°,AD是角平分线且AD=BD,AC=10. 求AB的长度.
提示:过点D作DE⊥AB于E
A
B
C
D
E
天生我才
三、小结
线段垂直平分线的性质:线段垂直平分线上的点到这条线段两个端点的距离相等。
线段垂直平分线的判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
谈谈你这节课的收获
