2022-2023学年人教版八年级数学上册 13.3.1等腰三角形 课件(共20页PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 13.3.1等腰三角形 课件(共20页PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 20:12:41 | ||
图片预览






文档简介
(共20张PPT)
13.3.1 等腰三角形
细心观察
生活中的等腰三角形
细心观察
北京五塔寺
A
B
C
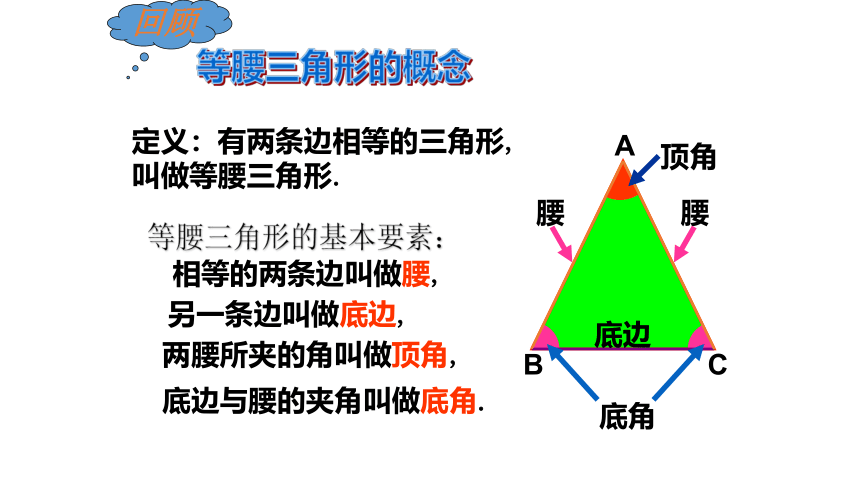
定义:有两条边相等的三角形,叫做等腰三角形.
等腰三角形的概念
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
回顾
等腰三角形的基本要素:
如图:把一张长方形纸片按图中的虚线对折,
并剪去红线下方的部分,再把它展 开,得△ABC
A
C
D
B
观察
AB 和AC有什么关系 这个三角形是什么三角形
AB=AC, △ABC是等腰三角形
心灵手巧
相信你:
A
B
C
D
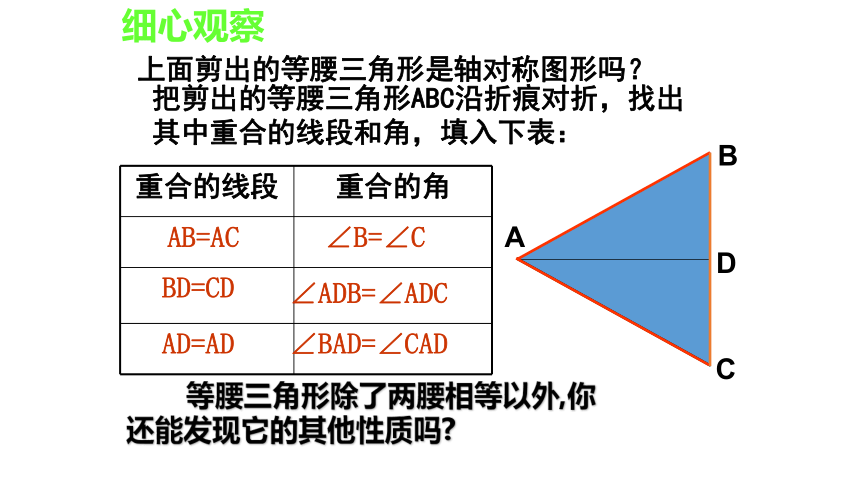
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角,填入下表:
重合的线段 重合的角
等腰三角形除了两腰相等以外,你还能发现它的其他性质吗
AB=AC
BD=CD
AD=AD
∠B=∠C
∠ADB=∠ADC
∠BAD=∠CAD
细心观察
上面剪出的等腰三角形是轴对称图形吗?
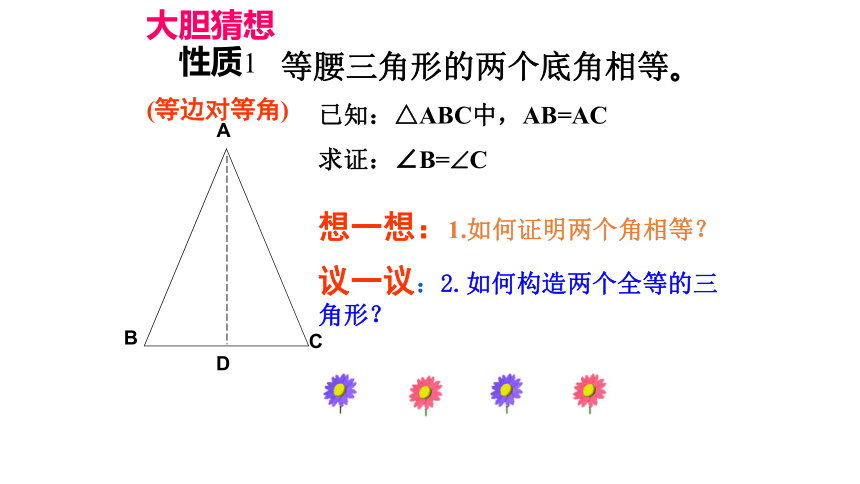
性质1
(等边对等角)
等腰三角形的两个底角相等。
A
B
C
D
已知:△ABC中,AB=AC
求证:∠B= C
想一想:1.如何证明两个角相等?
议一议:2.如何构造两个全等的三 角形?
大胆猜想
想一想:
刚才除了能得到∠B=∠C 你还能发现什么
重合的线段 重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB =∠ADC
=90°
AD是底边BC的中线
AD是顶角∠BAC的平分线
AD是底边BC 上的高
猜想二:
A
B
C
D
等腰三角形的顶角的平分线与底边上的中线,底边上的高互相重合(简称“三线合一”)
求证:等腰三角形的两个底角相等。
A
B
C
D
已知:△ABC中,AB=AC
求证:∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
等腰三角形性质1:
等腰三角形两个底角相等,
简称“等边对等角”
在△ABC中,∵ AB=AC
∴ =
数学语言
∠B
∠C
A
B
C
注意在同一个三角形中
A
B
C
D
等腰三角形性质2
等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)
性质2:在△ABC中, ( 1 ) ∵ AB=AC AD是角平分线,
∴ ⊥ , ____=_____ ;
( 2 ) ∵ AB=AC AD是中线,
∴ ⊥ ,∴∠ = ∠____;
( 3 ) ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CAD
BAD CAD
AD BC
AD BC
BD CD
BD CD
数学语言
注意:前提是在同一个等腰三角形中
导 入
示 标
预 习
探 究
达 标
提 升
1.在△ABC中,AB=AC,如果一个底
角为50°,则另两个角为____和____.
50° 80°
50°
50°
A
B
C
2.在△ABC中,AB=AC,如果一个角为50°,则另两个角为
________________________.
50°和 80°
或 65°和 65 °
导 入
示 标
预 习
探 究
达 标
提 升
3、在△ABC中,AB =AC,点D是BC的中点,
∠B = 40°,则∠BAD的度数是 .
50°
导 入
示 标
预 习
探 究
达 标
提 升
4、已知:如图,点D,E在△ABC的边BC上,
连接AD,AE,若AB=AC , AD=AE
求证:BD=CE
导 入
示 标
预 习
探 究
达 标
提 升
例1:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
D
C
B
A
(2)用含∠A的式子表示
∠CDB、∠C、∠ABC.
(3)求∠A的度数.
(1)图中有哪些等腰三角形?
导 入
示 标
预 习
探 究
达 标
提 升
点D在AC上,BD=BC=AD,
在△ABC中,∠A+∠ABC+∠ C=x+2x+2x=1800.
∴ x=360 , ∴ ∠A=360
在△ABC中,AB=AC,
求∠A的度数
解: ∵AB=AC, BD=BC=AD,
∴∠ ABC= ∠ C= ∠ BDC
∠ A = ∠ ABD(等边对等角)
∠A=x,则∠BDC= ∠A+∠ABD=2x
∴∠ABC= ∠C=∠BDC=2x
B
C
A
D
导 入
示 标
预 习
探 究
达 标
提 升
(1)本节课学习了哪些主要内容?
(2)我们是如何探究等腰三角形的性质的?
(3)本节课你学到了哪些证明线段相等或角相等的
方法?
13.3.1 等腰三角形
细心观察
生活中的等腰三角形
细心观察
北京五塔寺
A
B
C
定义:有两条边相等的三角形,叫做等腰三角形.
等腰三角形的概念
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
回顾
等腰三角形的基本要素:
如图:把一张长方形纸片按图中的虚线对折,
并剪去红线下方的部分,再把它展 开,得△ABC
A
C
D
B
观察
AB 和AC有什么关系 这个三角形是什么三角形
AB=AC, △ABC是等腰三角形
心灵手巧
相信你:
A
B
C
D
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角,填入下表:
重合的线段 重合的角
等腰三角形除了两腰相等以外,你还能发现它的其他性质吗
AB=AC
BD=CD
AD=AD
∠B=∠C
∠ADB=∠ADC
∠BAD=∠CAD
细心观察
上面剪出的等腰三角形是轴对称图形吗?
性质1
(等边对等角)
等腰三角形的两个底角相等。
A
B
C
D
已知:△ABC中,AB=AC
求证:∠B= C
想一想:1.如何证明两个角相等?
议一议:2.如何构造两个全等的三 角形?
大胆猜想
想一想:
刚才除了能得到∠B=∠C 你还能发现什么
重合的线段 重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB =∠ADC
=90°
AD是底边BC的中线
AD是顶角∠BAC的平分线
AD是底边BC 上的高
猜想二:
A
B
C
D
等腰三角形的顶角的平分线与底边上的中线,底边上的高互相重合(简称“三线合一”)
求证:等腰三角形的两个底角相等。
A
B
C
D
已知:△ABC中,AB=AC
求证:∠B= C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
等腰三角形性质1:
等腰三角形两个底角相等,
简称“等边对等角”
在△ABC中,∵ AB=AC
∴ =
数学语言
∠B
∠C
A
B
C
注意在同一个三角形中
A
B
C
D
等腰三角形性质2
等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)
性质2:在△ABC中, ( 1 ) ∵ AB=AC AD是角平分线,
∴ ⊥ , ____=_____ ;
( 2 ) ∵ AB=AC AD是中线,
∴ ⊥ ,∴∠ = ∠____;
( 3 ) ∵ AB=AC AD⊥BC,
∴∠_____=∠______,_____=______ 。
BAD CAD
BAD CAD
AD BC
AD BC
BD CD
BD CD
数学语言
注意:前提是在同一个等腰三角形中
导 入
示 标
预 习
探 究
达 标
提 升
1.在△ABC中,AB=AC,如果一个底
角为50°,则另两个角为____和____.
50° 80°
50°
50°
A
B
C
2.在△ABC中,AB=AC,如果一个角为50°,则另两个角为
________________________.
50°和 80°
或 65°和 65 °
导 入
示 标
预 习
探 究
达 标
提 升
3、在△ABC中,AB =AC,点D是BC的中点,
∠B = 40°,则∠BAD的度数是 .
50°
导 入
示 标
预 习
探 究
达 标
提 升
4、已知:如图,点D,E在△ABC的边BC上,
连接AD,AE,若AB=AC , AD=AE
求证:BD=CE
导 入
示 标
预 习
探 究
达 标
提 升
例1:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
D
C
B
A
(2)用含∠A的式子表示
∠CDB、∠C、∠ABC.
(3)求∠A的度数.
(1)图中有哪些等腰三角形?
导 入
示 标
预 习
探 究
达 标
提 升
点D在AC上,BD=BC=AD,
在△ABC中,∠A+∠ABC+∠ C=x+2x+2x=1800.
∴ x=360 , ∴ ∠A=360
在△ABC中,AB=AC,
求∠A的度数
解: ∵AB=AC, BD=BC=AD,
∴∠ ABC= ∠ C= ∠ BDC
∠ A = ∠ ABD(等边对等角)
∠A=x,则∠BDC= ∠A+∠ABD=2x
∴∠ABC= ∠C=∠BDC=2x
B
C
A
D
导 入
示 标
预 习
探 究
达 标
提 升
(1)本节课学习了哪些主要内容?
(2)我们是如何探究等腰三角形的性质的?
(3)本节课你学到了哪些证明线段相等或角相等的
方法?
