2022-2023学年人教版八年级数学上册12.1 全等三角形 课件 (共19张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.1 全等三角形 课件 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 17:14:14 | ||
图片预览






文档简介
(共19张PPT)
12.1 全等三角形
一、情景导入
一位哲人曾经说过:“世界上没有两片完全相同的叶子”,但是在我们的周围却有着好多形状,大小完全相同的图案,大家能举出这样的例子吗?
请观察,并说出你看到的现象
能够完全重合 的两个图形叫做全等形.
形状、大小相同的图形放在一起能够完全重合.
请观察下面两组图形,它们是不是全等图形?为什么?与同伴进行交流。
1
2
形状
不同
形状
相同
全等图形的特征:
全等图形的形状和大小必须都相同.
大小
不同
大小
不同
辩一辨
二、探究新知
活动一:请同学们和同桌一起将两本数学课本叠放在一起,观察它们能重合吗?
活动二:把准备好的三角形按在纸上,画出三角形,并裁下来,把原三角形和裁下来的三角形放在一起,观察它们能够重合吗?
全等三角形的定义:
能够完全重合的两个三角形叫做全等三角形.
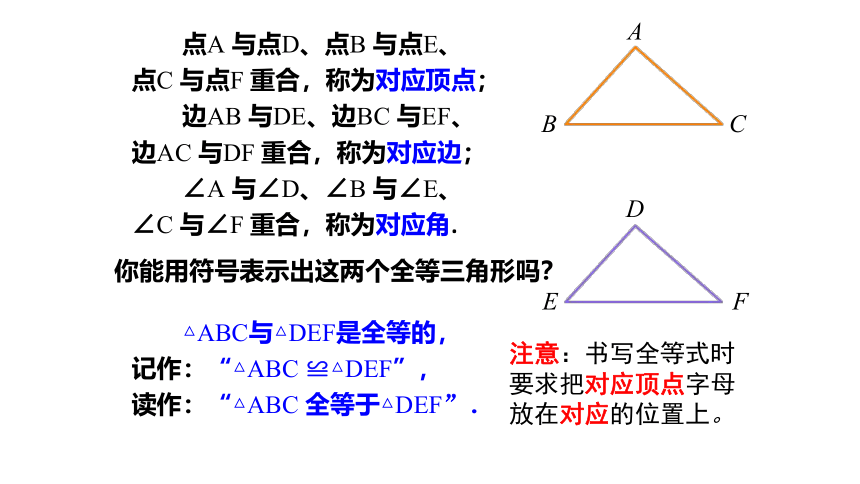
点A 与点D、点B 与点E、
点C 与点F 重合,称为对应顶点;
边AB 与DE、边BC 与EF、
边AC 与DF 重合,称为对应边;
∠A 与∠D、∠B 与∠E、
∠C 与∠F 重合,称为对应角.
A
B
C
D
E
F
你能用符号表示出这两个全等三角形吗?
△ABC与△DEF是全等的,
记作:“△ABC ≌△DEF”,
读作:“△ABC 全等于△DEF”.
注意:书写全等式时要求把对应顶点字母放在对应的位置上。
A
B
C
E
D
F
思考:下图中△ABC≌△DEF,对应边有什么关系?
对应角呢?
全等三角形的性质
全等三角形的对应角相等
全等三角形的对应边相等
∠A=∠D
∠B=∠E
∠C=∠F
AB=DE
BC=EF
AC=DF
∵△ABC≌△FDE
∴A B=F D,A C=F E,B C=D E(全等三角形对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E(全等三角形对应角相等)
A
B
C
E
D
F
全等三角形的性质的几何语言
A
B
C
D
写出全等式
△ABC ≌△DBC
BC的对应边是什么?
BC
A
B
C
D
写出全等式
△ABC ≌△DCB
BC的对应边是什么?
CB
探究归纳
A
B
C
D
小结三
△ABC ≌△FDE
E
F
(1)两个全等三角形最长的边是对应边:AC=FE
最短的边是对应边:AB=FD
(2)两个全等三角形最大的角是对应角:∠B=∠D
最小的角是对应角:∠C=∠E
找对应边、对应角的方法:
1、在两个全等三角形中一对最长的边(或最大的角)是对应边(或角);一对最短的边(或最小的角)是对应边(或角)。
2、公共角、对顶角必为对应角;公共边必为对应边。
3、对应角的对边为对应边;对应边的对角为对应角。
4、根据书写规范,按照对应顶点找对应边或对应角。
例1 如图,△ADE≌△BCF,AD=6 cm,CD=5 cm,求BD的长.
解:∵△ADE≌△BCF,∴AD=BC.∵AD=6 cm,
∴BC=6 cm.又∵CD=5 cm,
∴BD=BC-CD=6-5=1(cm).
典型例题
典型例题
例2:如图,已知ΔABC≌ΔFED, BC=ED, 证明:AB∥EF
证明: ∵ΔABC≌ΔFED ( )
∴∠ =∠ , ( )
∴ AB∥EF
将上述证明过程补充完整.
A
F
全等三角形的对应角相等
已知
证明:AD=CF
当堂检测
1.有下列说法: 全等三角形的形状相同; 周长
和面积都相等的两个三角形全等; 若两个钝角
三角形全等,则钝角所对的边是对应边;④两个
全等形无论怎样改变位置,都能够完全重合。
其中说法正确的个数有_______
3个
2.如图,将周长为8的△ABC
沿BC方向平移一个单位得
到△DEF,则四边形ABFD的
周长为_______
A
E
F
D
C
B
10
3,如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,有以下结论:其中正确的是( )
①AC=AE;
②∠FAB=∠EAB;
③EF=BC;
④∠EAB=∠FAC,
F
D
A
B
C
E
4,如图,△ABC≌△DEF,∠C=250,BC=6cm,AC=4cm,
你能得出△DEF中哪些角的大小,哪些边的长度
5,下列命题中正确的是( )
A.全等三角形的高相等
B.全等三角形的中线相等
C.全等三角形的角平分线相等
D.全等三角形的对应角平分线相等
互相重合的顶点叫做 。
互相重合的角叫做 。
互相重合的边叫做 。
其中
2、 叫做全等三角形。
1.能够重合的两个图形叫做 。
全等形
4.全等三角形的 和 相等
对应边
对应角
对应顶点
课 堂 小 结
能够重合的两个三角形
3.“全等”用符号“ ”来表示,读作“ ”
对应边
对应角
5.书写全等式时要求把对应字母放在对应
的位置上
全等于
≌
12.1 全等三角形
一、情景导入
一位哲人曾经说过:“世界上没有两片完全相同的叶子”,但是在我们的周围却有着好多形状,大小完全相同的图案,大家能举出这样的例子吗?
请观察,并说出你看到的现象
能够完全重合 的两个图形叫做全等形.
形状、大小相同的图形放在一起能够完全重合.
请观察下面两组图形,它们是不是全等图形?为什么?与同伴进行交流。
1
2
形状
不同
形状
相同
全等图形的特征:
全等图形的形状和大小必须都相同.
大小
不同
大小
不同
辩一辨
二、探究新知
活动一:请同学们和同桌一起将两本数学课本叠放在一起,观察它们能重合吗?
活动二:把准备好的三角形按在纸上,画出三角形,并裁下来,把原三角形和裁下来的三角形放在一起,观察它们能够重合吗?
全等三角形的定义:
能够完全重合的两个三角形叫做全等三角形.
点A 与点D、点B 与点E、
点C 与点F 重合,称为对应顶点;
边AB 与DE、边BC 与EF、
边AC 与DF 重合,称为对应边;
∠A 与∠D、∠B 与∠E、
∠C 与∠F 重合,称为对应角.
A
B
C
D
E
F
你能用符号表示出这两个全等三角形吗?
△ABC与△DEF是全等的,
记作:“△ABC ≌△DEF”,
读作:“△ABC 全等于△DEF”.
注意:书写全等式时要求把对应顶点字母放在对应的位置上。
A
B
C
E
D
F
思考:下图中△ABC≌△DEF,对应边有什么关系?
对应角呢?
全等三角形的性质
全等三角形的对应角相等
全等三角形的对应边相等
∠A=∠D
∠B=∠E
∠C=∠F
AB=DE
BC=EF
AC=DF
∵△ABC≌△FDE
∴A B=F D,A C=F E,B C=D E(全等三角形对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E(全等三角形对应角相等)
A
B
C
E
D
F
全等三角形的性质的几何语言
A
B
C
D
写出全等式
△ABC ≌△DBC
BC的对应边是什么?
BC
A
B
C
D
写出全等式
△ABC ≌△DCB
BC的对应边是什么?
CB
探究归纳
A
B
C
D
小结三
△ABC ≌△FDE
E
F
(1)两个全等三角形最长的边是对应边:AC=FE
最短的边是对应边:AB=FD
(2)两个全等三角形最大的角是对应角:∠B=∠D
最小的角是对应角:∠C=∠E
找对应边、对应角的方法:
1、在两个全等三角形中一对最长的边(或最大的角)是对应边(或角);一对最短的边(或最小的角)是对应边(或角)。
2、公共角、对顶角必为对应角;公共边必为对应边。
3、对应角的对边为对应边;对应边的对角为对应角。
4、根据书写规范,按照对应顶点找对应边或对应角。
例1 如图,△ADE≌△BCF,AD=6 cm,CD=5 cm,求BD的长.
解:∵△ADE≌△BCF,∴AD=BC.∵AD=6 cm,
∴BC=6 cm.又∵CD=5 cm,
∴BD=BC-CD=6-5=1(cm).
典型例题
典型例题
例2:如图,已知ΔABC≌ΔFED, BC=ED, 证明:AB∥EF
证明: ∵ΔABC≌ΔFED ( )
∴∠ =∠ , ( )
∴ AB∥EF
将上述证明过程补充完整.
A
F
全等三角形的对应角相等
已知
证明:AD=CF
当堂检测
1.有下列说法: 全等三角形的形状相同; 周长
和面积都相等的两个三角形全等; 若两个钝角
三角形全等,则钝角所对的边是对应边;④两个
全等形无论怎样改变位置,都能够完全重合。
其中说法正确的个数有_______
3个
2.如图,将周长为8的△ABC
沿BC方向平移一个单位得
到△DEF,则四边形ABFD的
周长为_______
A
E
F
D
C
B
10
3,如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,有以下结论:其中正确的是( )
①AC=AE;
②∠FAB=∠EAB;
③EF=BC;
④∠EAB=∠FAC,
F
D
A
B
C
E
4,如图,△ABC≌△DEF,∠C=250,BC=6cm,AC=4cm,
你能得出△DEF中哪些角的大小,哪些边的长度
5,下列命题中正确的是( )
A.全等三角形的高相等
B.全等三角形的中线相等
C.全等三角形的角平分线相等
D.全等三角形的对应角平分线相等
互相重合的顶点叫做 。
互相重合的角叫做 。
互相重合的边叫做 。
其中
2、 叫做全等三角形。
1.能够重合的两个图形叫做 。
全等形
4.全等三角形的 和 相等
对应边
对应角
对应顶点
课 堂 小 结
能够重合的两个三角形
3.“全等”用符号“ ”来表示,读作“ ”
对应边
对应角
5.书写全等式时要求把对应字母放在对应
的位置上
全等于
≌
