2022-2023学年人教版八年级数学上册 12.2.2 三角形全等的判定SAS 课件(共21页PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 12.2.2 三角形全等的判定SAS 课件(共21页PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 18:31:55 | ||
图片预览






文档简介
(共21张PPT)
12.2.2 三角形全等的判定SAS
链接生活:
小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?
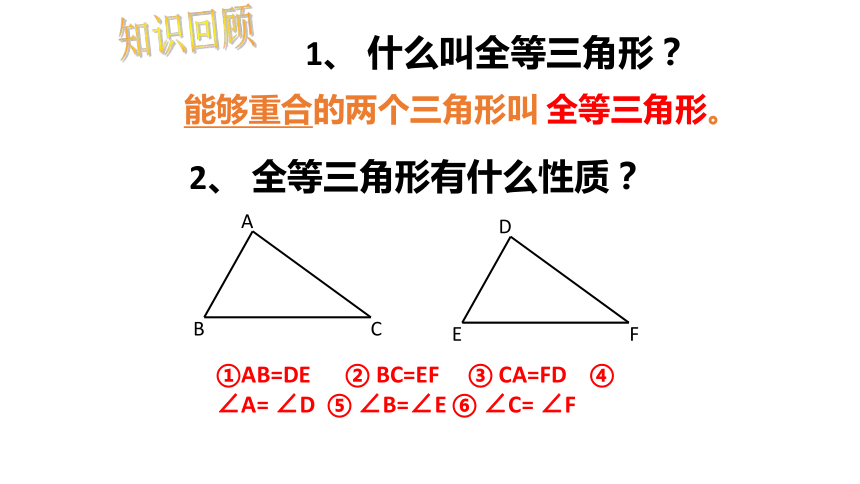
知识回顾
①AB=DE ② BC=EF ③ CA=FD ④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F
A
B
C
D
E
F
1、 什么叫全等三角形?
能够重合的两个三角形叫 全等三角形。
2、 全等三角形有什么性质?
一,画一个三角形ABC,使它的一个内角∠A=45°,夹这个角的两边AB=10cm,AC=8cm,
画法:
1.画一条线段AB=10cm
1.画∠MAB=45°
3.在射线AM上取AC=8cm
4.连接BC, △ABC 就是所求的三角形
把你画好的三角形剪下来准备好。
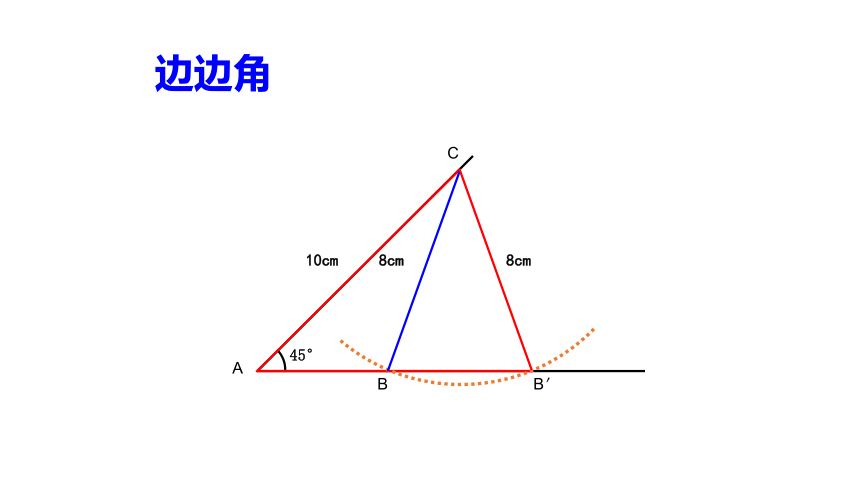
探究新知:(1)边角边
2.画一个△ABC,使它的一个内角∠A=45°这个角的邻边AC=10cm,这个角的对边BC=8cm,
画法:1.画∠MAN=45°
2.在AN上取AC=10cm
3.以点C为圆心,8cm为半径画弧交AM于点B,
4.连接BC, △ABC 就是所求的三角形
把你画好的三角形剪下来准备好。
探究新知:(2)边边角
A
45°
边边角
B
B′
C
10cm
8cm
8cm
10cm
A
B′
C
45°
8cm
边边角不能判定
两个三角形全等
B
A
8cm
45°
10cm
C
显然: △ABC与△AB′C不全等
结论:基本事实
如果两个三角形的两边和它们的夹角对应相等,那么这两个三角形全等。(简记为 “边角边”或SAS)。
注:“边边角”不能判定两个三角形全等
A
B
C
D
E
F
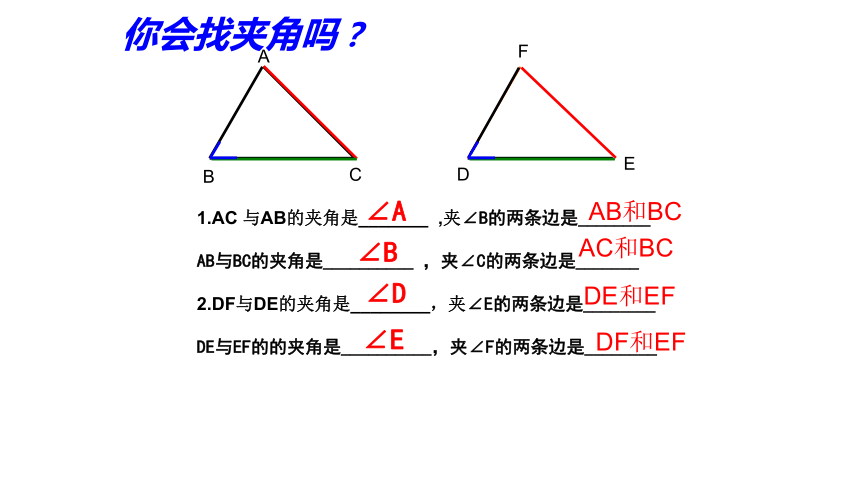
你会找夹角吗?
1.AC 与AB的夹角是_______ ,夹∠B的两条边是________
AB与BC的夹角是__________ ,夹∠C的两条边是_______
2.DF与DE的夹角是________,夹∠E的两条边是________
DE与EF的的夹角是__________,夹∠F的两条边是________
∠A
AB和BC
∠B
AC和BC
∠D
∠E
DE和EF
DF和EF
【例】已知:如图,AC=AD,∠CAB=∠DAB
求证:△ACB≌△ADB
AC=AD(已知)
∠CAB=∠DAB(已知)
AB=AB(公共边)
∴△ACB≌△ADB(SAS)
证明:在△ACB和△ADB中
A
B
C
D
1.如图,去修补一块玻璃,问带哪一块玻璃去可以使得新玻璃与原来的完全一样?
Ⅰ
Ⅱ
Ⅲ
知识应用
分析:带Ⅲ去,可以根据SAS得到与原三角形全等的一个三角形.
2.根据题中条件,分别找出各题中的全等三角形.
A
B
C
40°
D
E
F
(1)
(1)△ABC≌△EFD 根据“SAS”
(2)△ADC≌△CBA 根据“SAS”
40°
D
C
A
B
(2)
1:如图,∠BAC=∠CDB=90°,AC=DB,求证:AB=DC
B
C
D
A
证明: ∵∠BAC=∠CDB=90°(已知)
∴ΔBAC,ΔCDB都是直角三角形。
AC=DB(已知)
BC=BC(公共边)
∴Rt△ABC≌Rt△DCB(HL)。
∴ AB=DC(全等三角形对应边相等)
在Rt△ABC和Rt△DCB中,
分析:
巩固训练
2:如图,∠BAC=∠CDB=90°,请你再添加一个条件
使△ABC≌△DCB,并说明判定依据?
B
C
D
A
1.AB=DC(HL)
2.AC=DB(HL)
3.∠ABC=∠DCB(AAS)
4.∠ACB=∠DBC(AAS)
4 证明:全等三角形对应边上的高相等.
已知:如图,△ABC≌△A'B'C'.AD,A'D'分别是△ABC和△A'B'C'的高.求证:AD=A'D'.
例2 、有一湖泊,在湖泊的岸边有A、B两点,难以直接量出A,B两点之间的距离。你能设计一种量出A,B两点之间距离的方案吗?说明你这样设计的理由。
B
A
小试牛刀,深化理解
小试牛刀,深化理解
设计方案:先在湖泊边取一个能直接到达A和B处的点C,连结AC并延长至A′点,使AC= A′C,连结BC并延长至B′点,使BC= B′C,连结A′B′,用米尺量出A′B′的长,这个长度就等于A,B两点的距离。
·
A′
B
B′
A
C
理由:在△ABC与△A′B′C中
AC=A′C
∵ ∠ACB=∠A′CB′
BC=B′C
∴△ABC≌ △A′B′C (SAS)
∴A′B′=AB(全等三角形对应边相等)
变式训练
A
B
因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的尺子。请你设计一种方案,粗略测出A、B两杆之间的距离。
设计方案
A
B
先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结DE ,用尺子量出DE的长,这个长度就等于A,B两点的距离。
证明:在△ABC和△DEC中
AC=DC(已知)
∵ ∠ACB=∠DCE(对顶角相等)
BC=EC(已知)
∴ △ABC≌△DEC(SAS)
∴AB=DE(全等三角形的对应边相等)
·
C
D
E
A
B
C
D
A
B
C
D
2.已知:如图, △ABC中,AB=AC,AD是高
求证:BD=CD;∠BAD=∠CAD。
1.已知:如图,AC=AD,∠C,∠D是直角,求证:BC=BD。
C
D
A
B
课后练习
通过学习,需要我们掌握:
1.根据边角边定理判定两个三角形全等,要找出两边
及夹角对应相等的三个条件.
2.找使结论成立所需条件,要充分利用已知条件
(包括给出图形中的隐含条件,如公共边、公共角等),
并要善于运用学过的定义、公理、定理.
12.2.2 三角形全等的判定SAS
链接生活:
小明不小心打翻了墨水,将自己所画的三角形涂黑了,你能帮小明想想办法,画一个与原来完全一样的三角形吗?
知识回顾
①AB=DE ② BC=EF ③ CA=FD ④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F
A
B
C
D
E
F
1、 什么叫全等三角形?
能够重合的两个三角形叫 全等三角形。
2、 全等三角形有什么性质?
一,画一个三角形ABC,使它的一个内角∠A=45°,夹这个角的两边AB=10cm,AC=8cm,
画法:
1.画一条线段AB=10cm
1.画∠MAB=45°
3.在射线AM上取AC=8cm
4.连接BC, △ABC 就是所求的三角形
把你画好的三角形剪下来准备好。
探究新知:(1)边角边
2.画一个△ABC,使它的一个内角∠A=45°这个角的邻边AC=10cm,这个角的对边BC=8cm,
画法:1.画∠MAN=45°
2.在AN上取AC=10cm
3.以点C为圆心,8cm为半径画弧交AM于点B,
4.连接BC, △ABC 就是所求的三角形
把你画好的三角形剪下来准备好。
探究新知:(2)边边角
A
45°
边边角
B
B′
C
10cm
8cm
8cm
10cm
A
B′
C
45°
8cm
边边角不能判定
两个三角形全等
B
A
8cm
45°
10cm
C
显然: △ABC与△AB′C不全等
结论:基本事实
如果两个三角形的两边和它们的夹角对应相等,那么这两个三角形全等。(简记为 “边角边”或SAS)。
注:“边边角”不能判定两个三角形全等
A
B
C
D
E
F
你会找夹角吗?
1.AC 与AB的夹角是_______ ,夹∠B的两条边是________
AB与BC的夹角是__________ ,夹∠C的两条边是_______
2.DF与DE的夹角是________,夹∠E的两条边是________
DE与EF的的夹角是__________,夹∠F的两条边是________
∠A
AB和BC
∠B
AC和BC
∠D
∠E
DE和EF
DF和EF
【例】已知:如图,AC=AD,∠CAB=∠DAB
求证:△ACB≌△ADB
AC=AD(已知)
∠CAB=∠DAB(已知)
AB=AB(公共边)
∴△ACB≌△ADB(SAS)
证明:在△ACB和△ADB中
A
B
C
D
1.如图,去修补一块玻璃,问带哪一块玻璃去可以使得新玻璃与原来的完全一样?
Ⅰ
Ⅱ
Ⅲ
知识应用
分析:带Ⅲ去,可以根据SAS得到与原三角形全等的一个三角形.
2.根据题中条件,分别找出各题中的全等三角形.
A
B
C
40°
D
E
F
(1)
(1)△ABC≌△EFD 根据“SAS”
(2)△ADC≌△CBA 根据“SAS”
40°
D
C
A
B
(2)
1:如图,∠BAC=∠CDB=90°,AC=DB,求证:AB=DC
B
C
D
A
证明: ∵∠BAC=∠CDB=90°(已知)
∴ΔBAC,ΔCDB都是直角三角形。
AC=DB(已知)
BC=BC(公共边)
∴Rt△ABC≌Rt△DCB(HL)。
∴ AB=DC(全等三角形对应边相等)
在Rt△ABC和Rt△DCB中,
分析:
巩固训练
2:如图,∠BAC=∠CDB=90°,请你再添加一个条件
使△ABC≌△DCB,并说明判定依据?
B
C
D
A
1.AB=DC(HL)
2.AC=DB(HL)
3.∠ABC=∠DCB(AAS)
4.∠ACB=∠DBC(AAS)
4 证明:全等三角形对应边上的高相等.
已知:如图,△ABC≌△A'B'C'.AD,A'D'分别是△ABC和△A'B'C'的高.求证:AD=A'D'.
例2 、有一湖泊,在湖泊的岸边有A、B两点,难以直接量出A,B两点之间的距离。你能设计一种量出A,B两点之间距离的方案吗?说明你这样设计的理由。
B
A
小试牛刀,深化理解
小试牛刀,深化理解
设计方案:先在湖泊边取一个能直接到达A和B处的点C,连结AC并延长至A′点,使AC= A′C,连结BC并延长至B′点,使BC= B′C,连结A′B′,用米尺量出A′B′的长,这个长度就等于A,B两点的距离。
·
A′
B
B′
A
C
理由:在△ABC与△A′B′C中
AC=A′C
∵ ∠ACB=∠A′CB′
BC=B′C
∴△ABC≌ △A′B′C (SAS)
∴A′B′=AB(全等三角形对应边相等)
变式训练
A
B
因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的尺子。请你设计一种方案,粗略测出A、B两杆之间的距离。
设计方案
A
B
先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结DE ,用尺子量出DE的长,这个长度就等于A,B两点的距离。
证明:在△ABC和△DEC中
AC=DC(已知)
∵ ∠ACB=∠DCE(对顶角相等)
BC=EC(已知)
∴ △ABC≌△DEC(SAS)
∴AB=DE(全等三角形的对应边相等)
·
C
D
E
A
B
C
D
A
B
C
D
2.已知:如图, △ABC中,AB=AC,AD是高
求证:BD=CD;∠BAD=∠CAD。
1.已知:如图,AC=AD,∠C,∠D是直角,求证:BC=BD。
C
D
A
B
课后练习
通过学习,需要我们掌握:
1.根据边角边定理判定两个三角形全等,要找出两边
及夹角对应相等的三个条件.
2.找使结论成立所需条件,要充分利用已知条件
(包括给出图形中的隐含条件,如公共边、公共角等),
并要善于运用学过的定义、公理、定理.
