2022-2023学年北师大版数学八年级上册2.1《认识无理数》课件 (共21张PPT)
文档属性
| 名称 | 2022-2023学年北师大版数学八年级上册2.1《认识无理数》课件 (共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 513.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 22:42:34 | ||
图片预览







文档简介
(共21张PPT)
北师大版数学 八年级上册
第二章 实数
教学课件
1.认识无理数
教学目标
第二章 实数
1.认识并理解无理数的概念,能判断一个数是有理数还是无理数.(重点)
2.能用“夹逼法”估算无理数的近似值.(难点)
教学过程——温故知新
第二章 实数
1.什么是有理数?
2.有理数有哪些分类方法?
教学过程——新课引入
第二章 实数
议一议
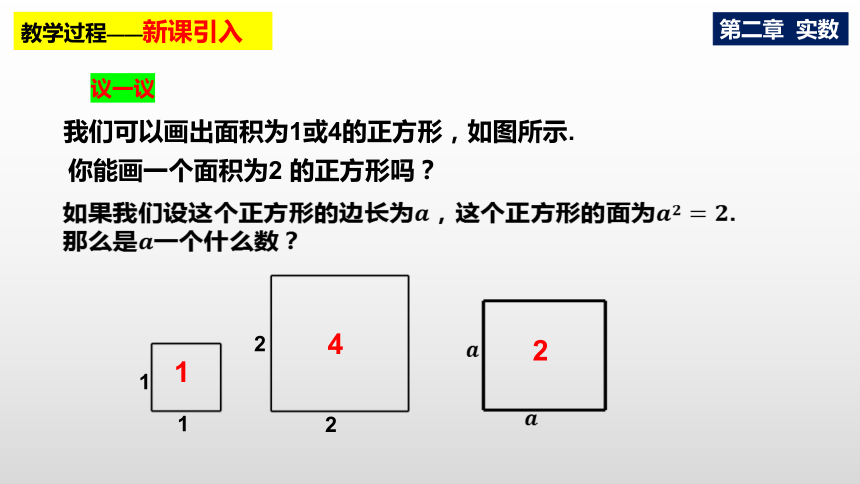
我们可以画出面积为1或4的正方形,如图所示.
1
1
2
2
你能画一个面积为2 的正方形吗?
如果我们设这个正方形的边长为,这个正方形的面为.那么是一个什么数?
1
4
2
教学过程——新知探究
第二章 实数
知识点1.非有理数
认识非有理数
我们可以利用学过的知识画出面积为2的正方形,如图.
1
1
我们线画一个直角边为1,斜边为的等腰直角三角形,如图.
再以直角三角形的斜边为边画一个正方形,如图.
此时正方形的面积为2=2.
2
教学过程——新知探究
第二章 实数
知识点1.非有理数
认识非有理数
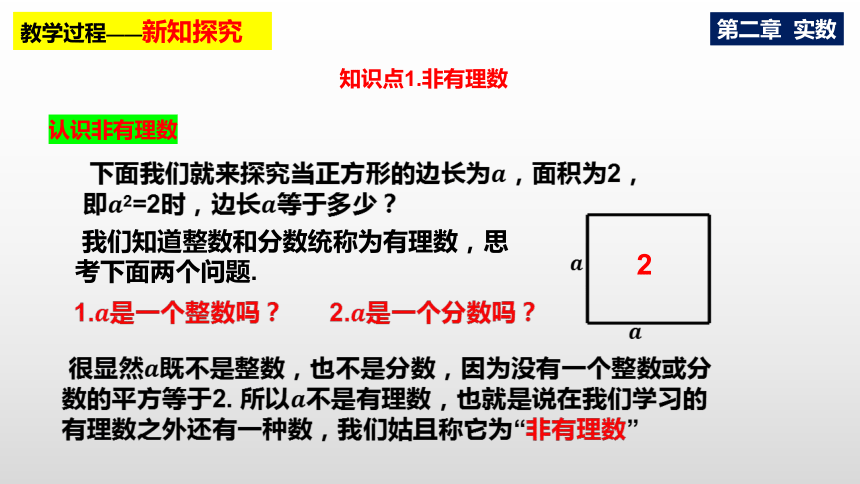
下面我们就来探究当正方形的边长为,面积为2,即2=2时,边长等于多少?
2
我们知道整数和分数统称为有理数,思考下面两个问题.
1.是一个整数吗?
2.是一个分数吗?
很显然既不是整数,也不是分数,因为没有一个整数或分数的平方等于2. 所以不是有理数,也就是说在我们学习的有理数之外还有一种数,我们姑且称它为“非有理数”
教学过程——新知探究
第二章 实数
知识点2.求非有理数的近似值
用“夹逼法”求非有理数的近似值
我们知道2=2中,是一个非有理数,我们如何求出的值呢?我们可以用如下的方法.
第一步:我们找到两个平方后最接近2的正整数,很显然12=1,22=4,平方后最接近2的正整数是1和2.
因为,所以1222,所以12.
第二步:我们取1和2的中间数1.5,因为1.52=2.25>2. 所以我们再取比1.5小的数1.4,因为1.42=1.96<2,所以1.
教学过程——新知探究
第二章 实数
知识点2.求非有理数的近似值
用“夹逼法”求非有理数的近似值
通过上面的两个步骤,我们已经找到当2=2时,是一个介于1.4与1.5之间的一个数,如果我们继续下去会发现1再继续 1 …… 最终=1.4142135623……
事实上无限制的继续下去会发现当2=2时,是一个永远不会循环的小数. 在粗略的计算中可以取≈1,或≈1.4或≈1.41 ……
我们把这种求非有理数的方法称为夹逼法.
教学过程——新知探究
第二章 实数
知识点3.认识无理数
1.无理数的概念
通过上面的探究发现2=2中的是一个无限不循环的小数,这类数在数的王国里还有很多,我们把这类数称为无理数.
无限不循环小数称为无理数.
目前我们学的无理数有以下几种类型:①既不是整数也不是分数的数(如0.2121121112……);②无限不循环的小数(如1.414213562……);③及含有的式子表示的数(如2,+5……).
注意:和有理数一样,无理数也分为正无理数和负无理数.
教学过程——新知探究
第二章 实数
知识点3.认识无理数
2.无理数和有理数的区别
因为整数可以看着是小数部分为0的小数,所有的分数都可以化为有限小数或无限不循环小数,反过来有限小数或无限不循环小数都可以化为整数或分数,所以说有理数就是有限小数或无限循环小数.
无理数是无限不循环小数,它不能化为分数,更不能化为整数. 所以有理数与无理数的根本区别在于有理数可以化为分数或整数,而无理数不能化为分数或整数.
教学过程——新知探究
第二章 实数
知识点3.认识无理数
3.分数的分类
通过上面的探究,我们可以把小数进行如下分类:
小数
有限小数(包含整数)
无限循环小数
无限循不环小数
有理数
无理数
无限小数
无限循环小数
无限循不环小数
教学过程——回归课本
第二章 实数
做一做
完成课本第21页“随堂练习”
教学过程——典例精析
第二章 实数
听一听
典例1
(1).下列正方形的边长是无理数的是( )
A. 面积为64的正方形 B. 面积为1.44的正方形
C. 面积为的正方形 D. 面积为的正方形
(2).下列数-3, 0, 3.14, 1.414232501…… , 2. , 0.3030030003……(每两个3之间依次增加一个0), 其中无理数有( )
A. 1个 B. 2个 C. 3个 D. 4个
D
C
(3).下列说法中,正确的个数为( )①无限小数都是无理数:②无限不循环小数都是无理数;③无理数都是无限小数:④无理数也有负数;⑤无理数分为正无理数、零、负无理数.A. 1个 B. 2个 C. 3个 D. 4个
教学过程——典例精析
第二章 实数
听一听
C
教学过程——典例精析
第二章 实数
听一听
(4).在每个小正方形边长都为1的网格中有△ABC,三角形的三个顶点都在格点上,则三角形的三边长为无理数的有( ).A. 3条 B. 2条 C.1条 D. 0条
A
B
C
B
教学过程——典例精析
第二章 实数
听一听
典例2 设边长为4的正方形的对角线长为.
(1)是有理数吗?说说你理由;
(2)请你估计一下在哪两个相邻整数之间?
(3)估计的值(结果精确到十分位);
(4)如果结果精确到百分位呢?
解:(1)根据勾股定理,得2=42+42=32 .
教学过程——典例精析
第二章 实数
听一听
∵没有一个整数的平方等于32,也没有一个分数的平方等于32,
∴既不是整数,也不是分数.
(2)∵52=25,62=36,25<32 <36,
∴52<2 <62,
∴5<<6.
(3)利用夹逼法可求得 .
(4)利用夹逼法可求得.
∴不是有理数.
教学过程——回归课本
第二章 实数
做一做
完成课本第24页“随堂练习”
教学过程——课堂小结
第二章 实数
记一记
1.无理数的概念
2.无理数与有理数的区别
课后巩固——分层作业
第二章 实数
练一练
第一层:课本第25页习题2.2第1、2、3题
第二层:课本第25页习题2.2第1、2、3题.
结束新课
感谢聆听
第二章 实数
北师大版数学 八年级上册
第二章 实数
教学课件
1.认识无理数
教学目标
第二章 实数
1.认识并理解无理数的概念,能判断一个数是有理数还是无理数.(重点)
2.能用“夹逼法”估算无理数的近似值.(难点)
教学过程——温故知新
第二章 实数
1.什么是有理数?
2.有理数有哪些分类方法?
教学过程——新课引入
第二章 实数
议一议
我们可以画出面积为1或4的正方形,如图所示.
1
1
2
2
你能画一个面积为2 的正方形吗?
如果我们设这个正方形的边长为,这个正方形的面为.那么是一个什么数?
1
4
2
教学过程——新知探究
第二章 实数
知识点1.非有理数
认识非有理数
我们可以利用学过的知识画出面积为2的正方形,如图.
1
1
我们线画一个直角边为1,斜边为的等腰直角三角形,如图.
再以直角三角形的斜边为边画一个正方形,如图.
此时正方形的面积为2=2.
2
教学过程——新知探究
第二章 实数
知识点1.非有理数
认识非有理数
下面我们就来探究当正方形的边长为,面积为2,即2=2时,边长等于多少?
2
我们知道整数和分数统称为有理数,思考下面两个问题.
1.是一个整数吗?
2.是一个分数吗?
很显然既不是整数,也不是分数,因为没有一个整数或分数的平方等于2. 所以不是有理数,也就是说在我们学习的有理数之外还有一种数,我们姑且称它为“非有理数”
教学过程——新知探究
第二章 实数
知识点2.求非有理数的近似值
用“夹逼法”求非有理数的近似值
我们知道2=2中,是一个非有理数,我们如何求出的值呢?我们可以用如下的方法.
第一步:我们找到两个平方后最接近2的正整数,很显然12=1,22=4,平方后最接近2的正整数是1和2.
因为,所以1222,所以12.
第二步:我们取1和2的中间数1.5,因为1.52=2.25>2. 所以我们再取比1.5小的数1.4,因为1.42=1.96<2,所以1.
教学过程——新知探究
第二章 实数
知识点2.求非有理数的近似值
用“夹逼法”求非有理数的近似值
通过上面的两个步骤,我们已经找到当2=2时,是一个介于1.4与1.5之间的一个数,如果我们继续下去会发现1再继续 1 …… 最终=1.4142135623……
事实上无限制的继续下去会发现当2=2时,是一个永远不会循环的小数. 在粗略的计算中可以取≈1,或≈1.4或≈1.41 ……
我们把这种求非有理数的方法称为夹逼法.
教学过程——新知探究
第二章 实数
知识点3.认识无理数
1.无理数的概念
通过上面的探究发现2=2中的是一个无限不循环的小数,这类数在数的王国里还有很多,我们把这类数称为无理数.
无限不循环小数称为无理数.
目前我们学的无理数有以下几种类型:①既不是整数也不是分数的数(如0.2121121112……);②无限不循环的小数(如1.414213562……);③及含有的式子表示的数(如2,+5……).
注意:和有理数一样,无理数也分为正无理数和负无理数.
教学过程——新知探究
第二章 实数
知识点3.认识无理数
2.无理数和有理数的区别
因为整数可以看着是小数部分为0的小数,所有的分数都可以化为有限小数或无限不循环小数,反过来有限小数或无限不循环小数都可以化为整数或分数,所以说有理数就是有限小数或无限循环小数.
无理数是无限不循环小数,它不能化为分数,更不能化为整数. 所以有理数与无理数的根本区别在于有理数可以化为分数或整数,而无理数不能化为分数或整数.
教学过程——新知探究
第二章 实数
知识点3.认识无理数
3.分数的分类
通过上面的探究,我们可以把小数进行如下分类:
小数
有限小数(包含整数)
无限循环小数
无限循不环小数
有理数
无理数
无限小数
无限循环小数
无限循不环小数
教学过程——回归课本
第二章 实数
做一做
完成课本第21页“随堂练习”
教学过程——典例精析
第二章 实数
听一听
典例1
(1).下列正方形的边长是无理数的是( )
A. 面积为64的正方形 B. 面积为1.44的正方形
C. 面积为的正方形 D. 面积为的正方形
(2).下列数-3, 0, 3.14, 1.414232501…… , 2. , 0.3030030003……(每两个3之间依次增加一个0), 其中无理数有( )
A. 1个 B. 2个 C. 3个 D. 4个
D
C
(3).下列说法中,正确的个数为( )①无限小数都是无理数:②无限不循环小数都是无理数;③无理数都是无限小数:④无理数也有负数;⑤无理数分为正无理数、零、负无理数.A. 1个 B. 2个 C. 3个 D. 4个
教学过程——典例精析
第二章 实数
听一听
C
教学过程——典例精析
第二章 实数
听一听
(4).在每个小正方形边长都为1的网格中有△ABC,三角形的三个顶点都在格点上,则三角形的三边长为无理数的有( ).A. 3条 B. 2条 C.1条 D. 0条
A
B
C
B
教学过程——典例精析
第二章 实数
听一听
典例2 设边长为4的正方形的对角线长为.
(1)是有理数吗?说说你理由;
(2)请你估计一下在哪两个相邻整数之间?
(3)估计的值(结果精确到十分位);
(4)如果结果精确到百分位呢?
解:(1)根据勾股定理,得2=42+42=32 .
教学过程——典例精析
第二章 实数
听一听
∵没有一个整数的平方等于32,也没有一个分数的平方等于32,
∴既不是整数,也不是分数.
(2)∵52=25,62=36,25<32 <36,
∴52<2 <62,
∴5<<6.
(3)利用夹逼法可求得 .
(4)利用夹逼法可求得.
∴不是有理数.
教学过程——回归课本
第二章 实数
做一做
完成课本第24页“随堂练习”
教学过程——课堂小结
第二章 实数
记一记
1.无理数的概念
2.无理数与有理数的区别
课后巩固——分层作业
第二章 实数
练一练
第一层:课本第25页习题2.2第1、2、3题
第二层:课本第25页习题2.2第1、2、3题.
结束新课
感谢聆听
第二章 实数
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
