2022-2023学年人教版七年级数学上册3.1.2 一元一次方程-等式的性质 课件 (共16张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学上册3.1.2 一元一次方程-等式的性质 课件 (共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 201.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 22:46:55 | ||
图片预览





文档简介
(共16张PPT)
等式的性质
第三单元 一元一次方程
导入新课
讲授新课
当堂练习
课堂小结
初中数学
七年级 上册
1.通过等式的性质解方程(重点)。
2.由具体实例抽象出等式的性质(难点)。
学习目标
为了讨论解方程,我们先看看等式有什么性质?
提 问
下列四个式子有什么相同点
用等号表示相等关系的式子,叫等式。
观察与思考
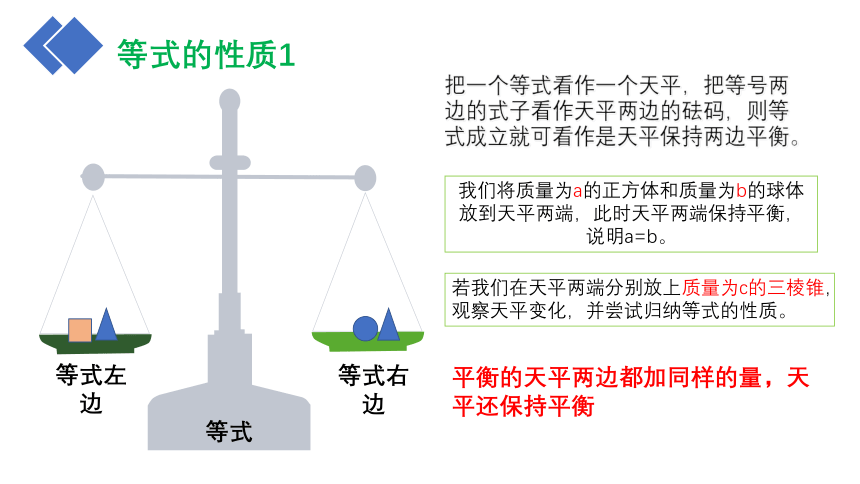
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
我们将质量为a的正方体和质量为b的球体放到天平两端,此时天平两端保持平衡,说明a=b。
若我们在天平两端分别放上质量为c的三棱锥,观察天平变化,并尝试归纳等式的性质。
等式
等式左边
等式右边
平衡的天平两边都加同样的量,天平还保持平衡
等式的性质1
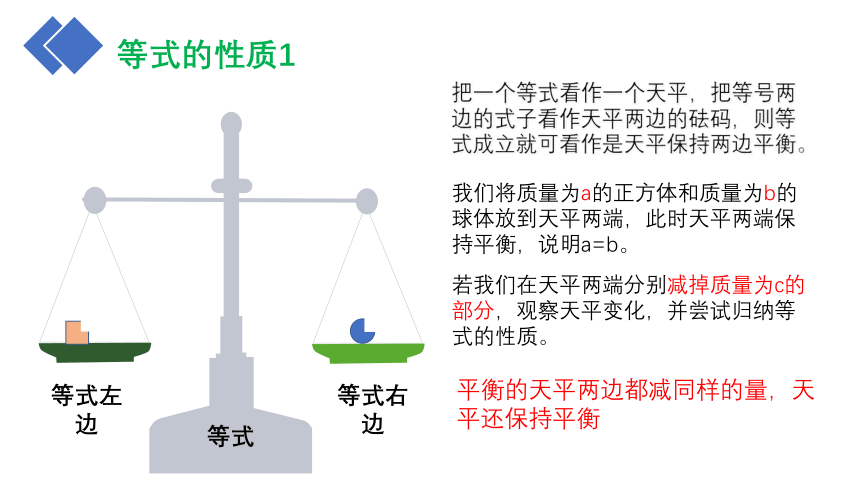
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
我们将质量为a的正方体和质量为b的球体放到天平两端,此时天平两端保持平衡,说明a=b。
若我们在天平两端分别减掉质量为c的部分,观察天平变化,并尝试归纳等式的性质。
等式
等式左边
等式右边
平衡的天平两边都减同样的量,天平还保持平衡
等式的性质1
等式的两边都加上(或减去)同一个数(或同一个式子),所得的结果仍是等式。
表示为:如果a=b,那么a ± c=a ± c
小结
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
我们将质量为a的正方体和质量为b的球体放到天平两端,此时天平两端保持平衡,说明a=b。
若我们在天平两端分别放上两个质量为a的正方体及质量为b的球体,观察天平变化,并尝试归纳等式的性质。
等式
等式左边
等式右边
平衡的天平两边都乘同一个数,天平还保持平衡
等式的性质2
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
我们将质量为a的正方体和质量为b的球体放到天平两端,此时天平两段保持平衡,说明a=b。
若我们在天平两端分别去掉正方体及球体一半质量,观察天平变化,并尝试归纳等式的性质。
等式
等式左边
等式右边
平衡的天平两边都除以同一个不为0的数
天平还保持平衡
等式的性质2
如果 a=b ,那么ac = bc
如果 a=b(c≠0),那么 =
等式两边都乘以同一个数,或都除以同一个不为0的数,结果仍相等。
小结
1、等式两边都要参加运算,并且是作同一种运算。
2、等式两边加或减,乘或除以的数一定是同一个数或
同一个式子。
3、等式两边不能都除以0,即0不能作除数或分母.
注意
解:(1)两边减7得
(2)两边同时除以-5得
(3)两边加5,得
化简得:
两边同乘-3,得
解以x为未知数的方程,就是把方程逐步转化为x=a(常数)的形式,等式的性质是转化的重要依据。
用等式的性质解方程
根据 。
(3)如果4x=-12y,那么x= ,
(4)如果-0.2x=4,那么x= ,
根据 。
等式性质1,在等式两边同加3
等式性质2,在等式两边同时除以4
等式性质2,在等式两边同除-0.2或乘-5
(2)如果x-3=4,那么x-3+3=_______,
3×0.5
根据 。
根据 。
4+3
等式性质2,在等式两边同时乘3
-3y
-20
课堂测试
已知a=b,下列变形正确的有( )个.
①a+c=b+c;②a﹣c=b﹣c;③3a=3b;④ac=bc;⑤
A.5 B.4 C.3 D.2
①根据等式性质1,两边同时加上c得:a+c=b+c,故①正确;
②根据等式性质1,两边同时减去c得:a﹣c=b﹣c,故②正确;
③根据等式的性质2,两边同时乘以3,3a=3b,故③正确;
④根据等式的性质2,两边同时乘以c,ac=bc,故④正确;
⑤因为c可能为0,所以 与 不一定相等,故⑤不正确.
故选:B.
课堂测试
已知2x﹣3y=4,则x﹣1.5y=_____.
课堂测试
谢谢!
等式的性质
第三单元 一元一次方程
导入新课
讲授新课
当堂练习
课堂小结
初中数学
七年级 上册
1.通过等式的性质解方程(重点)。
2.由具体实例抽象出等式的性质(难点)。
学习目标
为了讨论解方程,我们先看看等式有什么性质?
提 问
下列四个式子有什么相同点
用等号表示相等关系的式子,叫等式。
观察与思考
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
我们将质量为a的正方体和质量为b的球体放到天平两端,此时天平两端保持平衡,说明a=b。
若我们在天平两端分别放上质量为c的三棱锥,观察天平变化,并尝试归纳等式的性质。
等式
等式左边
等式右边
平衡的天平两边都加同样的量,天平还保持平衡
等式的性质1
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
我们将质量为a的正方体和质量为b的球体放到天平两端,此时天平两端保持平衡,说明a=b。
若我们在天平两端分别减掉质量为c的部分,观察天平变化,并尝试归纳等式的性质。
等式
等式左边
等式右边
平衡的天平两边都减同样的量,天平还保持平衡
等式的性质1
等式的两边都加上(或减去)同一个数(或同一个式子),所得的结果仍是等式。
表示为:如果a=b,那么a ± c=a ± c
小结
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
我们将质量为a的正方体和质量为b的球体放到天平两端,此时天平两端保持平衡,说明a=b。
若我们在天平两端分别放上两个质量为a的正方体及质量为b的球体,观察天平变化,并尝试归纳等式的性质。
等式
等式左边
等式右边
平衡的天平两边都乘同一个数,天平还保持平衡
等式的性质2
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等式成立就可看作是天平保持两边平衡。
我们将质量为a的正方体和质量为b的球体放到天平两端,此时天平两段保持平衡,说明a=b。
若我们在天平两端分别去掉正方体及球体一半质量,观察天平变化,并尝试归纳等式的性质。
等式
等式左边
等式右边
平衡的天平两边都除以同一个不为0的数
天平还保持平衡
等式的性质2
如果 a=b ,那么ac = bc
如果 a=b(c≠0),那么 =
等式两边都乘以同一个数,或都除以同一个不为0的数,结果仍相等。
小结
1、等式两边都要参加运算,并且是作同一种运算。
2、等式两边加或减,乘或除以的数一定是同一个数或
同一个式子。
3、等式两边不能都除以0,即0不能作除数或分母.
注意
解:(1)两边减7得
(2)两边同时除以-5得
(3)两边加5,得
化简得:
两边同乘-3,得
解以x为未知数的方程,就是把方程逐步转化为x=a(常数)的形式,等式的性质是转化的重要依据。
用等式的性质解方程
根据 。
(3)如果4x=-12y,那么x= ,
(4)如果-0.2x=4,那么x= ,
根据 。
等式性质1,在等式两边同加3
等式性质2,在等式两边同时除以4
等式性质2,在等式两边同除-0.2或乘-5
(2)如果x-3=4,那么x-3+3=_______,
3×0.5
根据 。
根据 。
4+3
等式性质2,在等式两边同时乘3
-3y
-20
课堂测试
已知a=b,下列变形正确的有( )个.
①a+c=b+c;②a﹣c=b﹣c;③3a=3b;④ac=bc;⑤
A.5 B.4 C.3 D.2
①根据等式性质1,两边同时加上c得:a+c=b+c,故①正确;
②根据等式性质1,两边同时减去c得:a﹣c=b﹣c,故②正确;
③根据等式的性质2,两边同时乘以3,3a=3b,故③正确;
④根据等式的性质2,两边同时乘以c,ac=bc,故④正确;
⑤因为c可能为0,所以 与 不一定相等,故⑤不正确.
故选:B.
课堂测试
已知2x﹣3y=4,则x﹣1.5y=_____.
课堂测试
谢谢!
