2022-2023学年人教版七年级数学上册 3.1.2等式的性质 课件(共14张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学上册 3.1.2等式的性质 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 06:47:28 | ||
图片预览



文档简介
(共14张PPT)
第三章 一元一次方程
3.1 从算式到方程
3.1.2 等式的性质
复习回顾
1、什么叫方程?什么叫一元一次方程?
2、什么叫方程的解?
含有未知数的等式叫做方程
只含有一个未知数,
未知数的次数是1的整式方程叫做一元一次方程
使方程左右两边相等的未知
数的值叫方程的解.
提出问题
能否用估算法求出下列方程的解
(2) 3x -7= 17
(1) 4x=12
(3) 0.17x-0.23x=0.11x+3.4
第(3)题估算起来比较困难,所以我们必须学习解一元一次方程的其他方法
学习新知
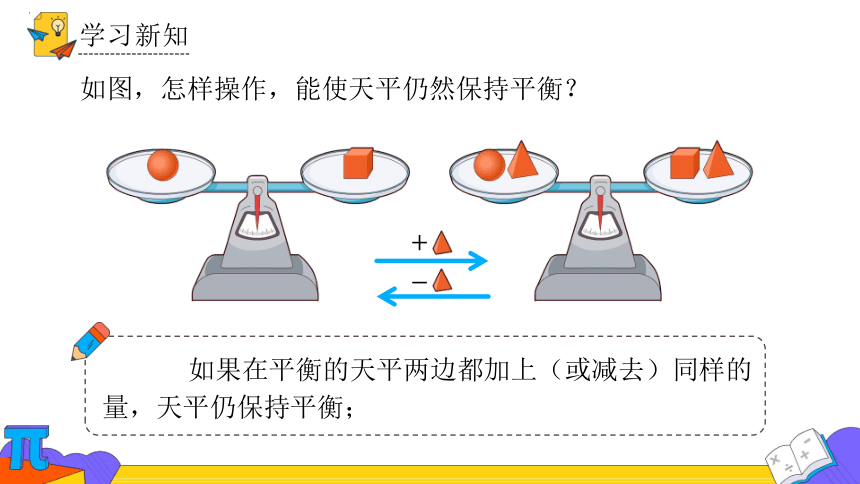
如图,怎样操作,能使天平仍然保持平衡?
如果在平衡的天平两边都加上(或减去)同样的量,天平仍保持平衡;
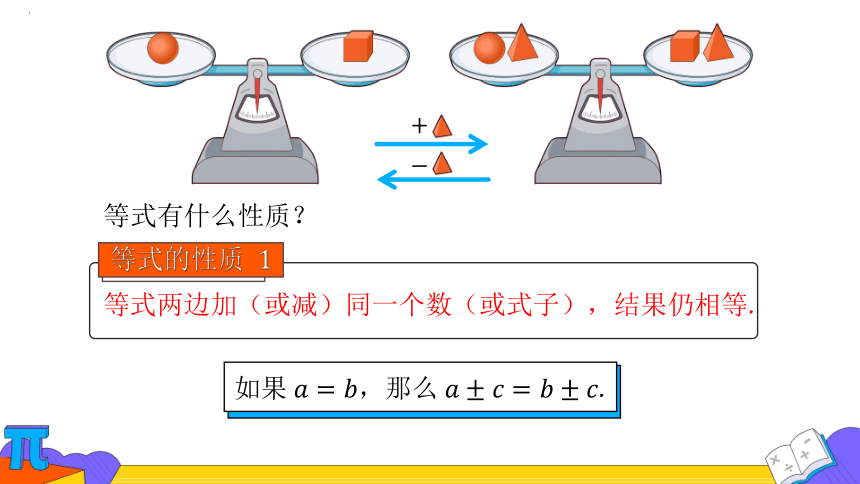
如果,那么.
等式两边加(或减)同一个数(或式子),结果仍相等.
等式的性质
等式有什么性质?
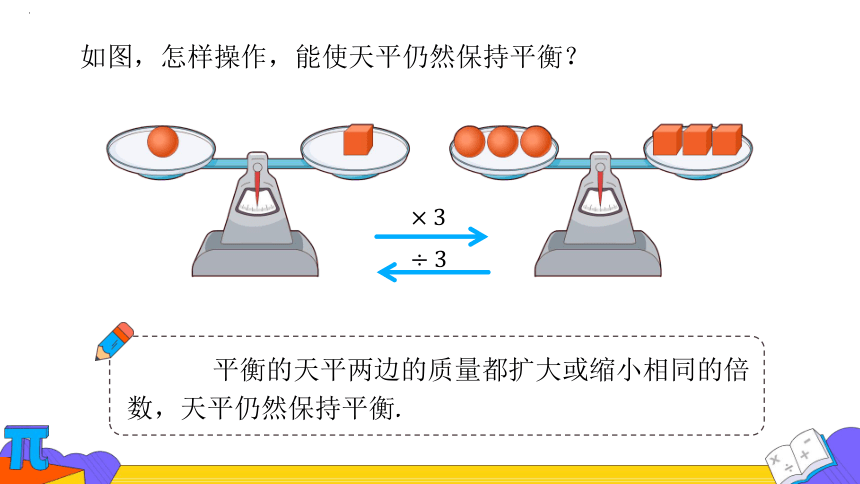
如图,怎样操作,能使天平仍然保持平衡?
平衡的天平两边的质量都扩大或缩小相同的倍数,天平仍然保持平衡.
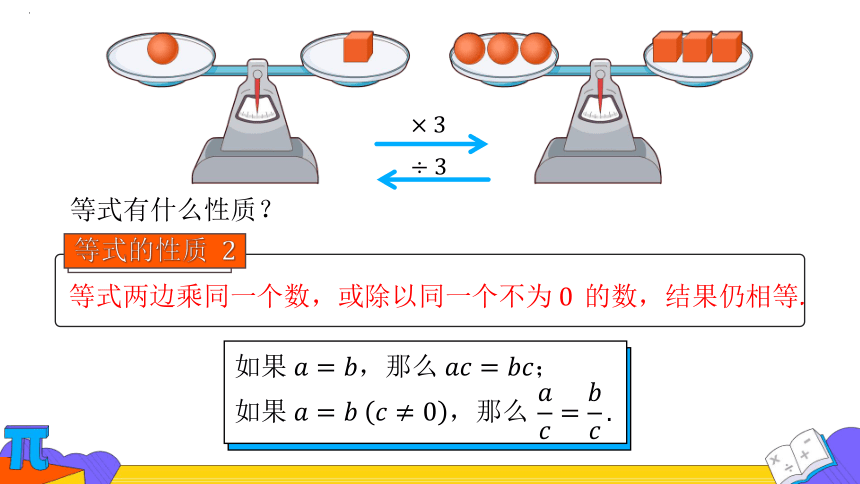
等式有什么性质?
等式两边乘同一个数,或除以同一个不为 的数,结果仍相等.
等式的性质
如果,那么;
如果,那么
等式的性质
性质1: 等式两边加(或减)同一个数(或式子), 结果仍相等.
性质2: 等式两边乘同一个数, 或除以同一个不为0的数, 结果仍相等.
注意:(1)等式两边同加减同乘除,即同时进行同一种运算
(2)等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
(3)等式两边不能除以0,即0不能作除数或分母.
(2) 怎样从等式 3+x=1 得到等式 x =-2
(3) 怎样从等式 4x=12 得到等式 x =3
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
例1 (1) 怎样从等式 x-5= y-5 得到等式 x = y
依据等式的性质1两边同时加5.
典例精析
(4) 怎样从等式 得到等式 a = b
等式的性质的应用
(2) 从 a+2=b+2 能不能得到 a=b,为什么
(3) 从-3a=-3b 能不能得到 a=b,为什么
(4) 从 3ac=4a 能不能得到 3c=4,为什么
说一说
(1) 从 x = y 能不能得到 ,为什么
能,根据等式的性质2,两边同时除以9
能,根据等式的性质1,两边同时加上2
能,根据等式的性质2,两边同时除以-3
不能,a可能为0
以下是某同学的变形过程,请找出变形过程中的错误.
已知
解:
两边加 ,得.
两边减 ,得.
两边除以,得.
分析
可知 不能做除数.
当堂练习
当堂练习
A
2. 下列各式变形正确的是 ( )
A. 由3x-1= 2x+1得3x-2x =1+1
B. 由5+1= 6得5= 6+1
C. 由2(x+1) = 2y+1得x +1= y +1
D. 由2a + 3b = c-6 得2a = c-18b
1. 下列说法正确的是_______
A. 等式都是方程
B. 方程都是等式
C. 不是方程的就不是等式
D. 未知数的值就是方程的解
B
3. 下列变形,正确的是 ( )
A. 若ac = bc,则a = b
B. 若 ,则a = b
C. 若a2 = b2,则a = b
D. 若 ,则x = -2
B
如果,那么.
等式两边加(或减)同一个数(或式子),结果仍相等.
等式的性质
等式两边乘同一个数,或除以同一个不为 的数,结果仍相等.
等式的性质
如果,那么;
如果,那么
课
堂
小
结
第三章 一元一次方程
3.1 从算式到方程
3.1.2 等式的性质
复习回顾
1、什么叫方程?什么叫一元一次方程?
2、什么叫方程的解?
含有未知数的等式叫做方程
只含有一个未知数,
未知数的次数是1的整式方程叫做一元一次方程
使方程左右两边相等的未知
数的值叫方程的解.
提出问题
能否用估算法求出下列方程的解
(2) 3x -7= 17
(1) 4x=12
(3) 0.17x-0.23x=0.11x+3.4
第(3)题估算起来比较困难,所以我们必须学习解一元一次方程的其他方法
学习新知
如图,怎样操作,能使天平仍然保持平衡?
如果在平衡的天平两边都加上(或减去)同样的量,天平仍保持平衡;
如果,那么.
等式两边加(或减)同一个数(或式子),结果仍相等.
等式的性质
等式有什么性质?
如图,怎样操作,能使天平仍然保持平衡?
平衡的天平两边的质量都扩大或缩小相同的倍数,天平仍然保持平衡.
等式有什么性质?
等式两边乘同一个数,或除以同一个不为 的数,结果仍相等.
等式的性质
如果,那么;
如果,那么
等式的性质
性质1: 等式两边加(或减)同一个数(或式子), 结果仍相等.
性质2: 等式两边乘同一个数, 或除以同一个不为0的数, 结果仍相等.
注意:(1)等式两边同加减同乘除,即同时进行同一种运算
(2)等式两边加或减,乘或除以的数一定是同一个数或同一个式子.
(3)等式两边不能除以0,即0不能作除数或分母.
(2) 怎样从等式 3+x=1 得到等式 x =-2
(3) 怎样从等式 4x=12 得到等式 x =3
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
例1 (1) 怎样从等式 x-5= y-5 得到等式 x = y
依据等式的性质1两边同时加5.
典例精析
(4) 怎样从等式 得到等式 a = b
等式的性质的应用
(2) 从 a+2=b+2 能不能得到 a=b,为什么
(3) 从-3a=-3b 能不能得到 a=b,为什么
(4) 从 3ac=4a 能不能得到 3c=4,为什么
说一说
(1) 从 x = y 能不能得到 ,为什么
能,根据等式的性质2,两边同时除以9
能,根据等式的性质1,两边同时加上2
能,根据等式的性质2,两边同时除以-3
不能,a可能为0
以下是某同学的变形过程,请找出变形过程中的错误.
已知
解:
两边加 ,得.
两边减 ,得.
两边除以,得.
分析
可知 不能做除数.
当堂练习
当堂练习
A
2. 下列各式变形正确的是 ( )
A. 由3x-1= 2x+1得3x-2x =1+1
B. 由5+1= 6得5= 6+1
C. 由2(x+1) = 2y+1得x +1= y +1
D. 由2a + 3b = c-6 得2a = c-18b
1. 下列说法正确的是_______
A. 等式都是方程
B. 方程都是等式
C. 不是方程的就不是等式
D. 未知数的值就是方程的解
B
3. 下列变形,正确的是 ( )
A. 若ac = bc,则a = b
B. 若 ,则a = b
C. 若a2 = b2,则a = b
D. 若 ,则x = -2
B
如果,那么.
等式两边加(或减)同一个数(或式子),结果仍相等.
等式的性质
等式两边乘同一个数,或除以同一个不为 的数,结果仍相等.
等式的性质
如果,那么;
如果,那么
课
堂
小
结
