2022-2023学年人教版七年级数学上册 3.2 一元一次方程- 合并同类项与移项 课件 (共23张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学上册 3.2 一元一次方程- 合并同类项与移项 课件 (共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 324.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 06:49:21 | ||
图片预览








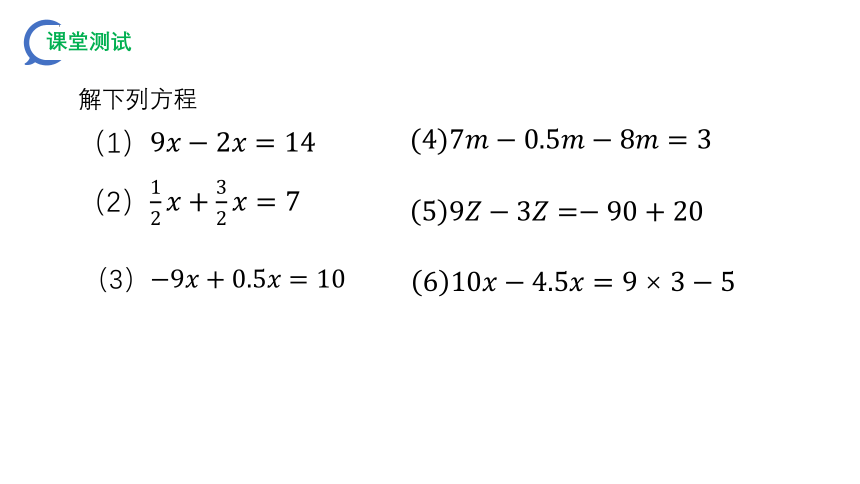
文档简介
(共23张PPT)
解一元一次方程(合并同类项-移项)
第三单元 一元一次方程
导入新课
讲授新课
当堂练习
课堂小结
初中数学
七年级 上册
例:将下列各式合并同类项
解:(1)
(2)
(3)
5
同类项
所含字母相同
相同字母的指数也相同
合并同类项
字母部分不变
系数相加减
合并同类项知识点回顾
前年购买量+去年购买量+今年购买量=140台
x + 2 x + 4 x =140
分析:
2.数量关系:
4.转化为方程:
3.相等关系:
问题:某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
1 .设未知数:
前年购买台数 去年购买台数 今年购买台数
x
2x
4x
“各部分量的和=总量”是一个基本的相等关系
思考
问题:某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
设前年购买电脑台数为x台
x+2x+4x=140
分析:解方程,就是把方程变形为 x = a(a为常数)的形式.
合并同类项
7x=140
系数化为1(利用等式的基本性质2,方程左右两边同时除以7)
x=20
思考
上面解方程中“合并同类项起了什么作用?
合并同类项起到了“ 化简”的作用,
把含有未知数的项合并为一项,
从而把方程转化为ax=b,
使其更接近x=a的形式
(其中a,b是常数) .
思考
例1:解下列方程
解:
解:
(等式两边同时除以-3)
(等式两边同时乘以-2)
思考
例2:三个连续整数的和等于27,求这三个数。
设第一个数为x,则第二个数为x+1,第三个数为x+2
x+x+1+x+2=27
合并同类项
等式的性质1
3x+3=27
3x+3-3=27-3
系数化为1
x=8
则这三个数分别是8、9、10
思考
列方程解应用题分哪些步骤?
①审:审清题意
②设:设出合理的未知数
③找:找出相等关系
④列:列出方程
⑤解:求出方程的解
⑦答:作答
⑥验:检验答案是否正确
小结
解下列方程
(2)
(1)
(3)
课堂测试
一个足球的表面一共有32个皮块,黑色与白色皮块的数目比为3:5,你能求出黑色皮块和白色皮块各有多少吗?
解:设黑色皮块有3x个,
则白色皮块有5x个,
依题意,得
分析:黑色皮块+白色皮块=32个皮块
3x+5x=32
合并同类项,得
8x=32
x=4
系数化为1,得
答:黑色皮块有12个,白色皮块有20个。
3x=12
5x=20
所以
课堂测试
太阳下山晚霞红,我把鸭子赶回笼;一半在外闹哄哄,一半的一半进笼中;剩下十五围着我,请算多少帮我忙。你能列出方程来解决这个问题吗?
解:设有鸭子x只
探索提高
把一些图书分给七(3)班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
分析:
设这个班有x名学生.
每人分3本,还剩余20本,则这批书共 本;
每人分4本,还缺25本,则这批书共 本;
(3x+20)
(4x-25)
3x+20=4x-25
(4)根据题意可列方程为________________________
因为这批书的总数是一个定值,
表示它的两个式子应相等
等式左右两边都有未知数,
如何求得方程的解呢?
思 考
如何求方程3x+20=4x-25的解?
把它变成x=a(常数)的形式
3x+20 = 4x-25
等式两边都含有
x的项和不含字母的常数项。
利用等式性质1,将等式
变为x=a(常数)的形式
3x+20-4x-20=4x-25-4x-20
3x-4x=-25-20
-x=-45
合并同类项
x=45
思 考
3x+20 = 4x-25
3x-4x = -25-20
下面方程的变形,把某项从等式的一边移动到另一边时有什么变化?
把等式一边的某项变号后移到另一边,叫做移项.
符号发生变化
移项的依据:
等式的性质1
观察
判断下面的移项是否正确?
(1) 10+x=10 移项,得 x=10+10
(2) 3x=x-5 移项,得 3x+x=-5
(3) 3x=6-2x 移项,得 3x+2x=-6
(4) 1-2x=-3x 移项,得 3x-2x=-1
(5) 2x+8=12-6x 移项,得 2x+6x=12-8
知识巩固
上述解方程中“ 移项”起了什么作用?
解方程时经常要“ 合并同类项”和“移项”,已达到化简的目的。
思 考
(1)3x+7=32-2x
解:
移项得:
3x+2x=32-7
合并同类项,得
5x=25
系数化为1,得
x=5
解:
移项,得:
合并同类项,得:
系数化为1,得
x=-8
解方程时注意移项后
符号发生变化
解方程
1.小亮在计算 41-N 时,误将“ -”看成“ +”,结果得13,则41-N的值应为( )
A.-28 B.54 C.69 D.-54
根据题意,41+N=13,
移项后解得N=-28,
∴41-N=41-(-28)=69.
故选C.
课堂测试
2.(1)当x取何值时,2x+3与-5x+6相等?
2x+3=-5x+6
移项得, 2x+5x= 6-3
合并同类项得, 7x=3
系数化为1得, x=
(2)当x取何值时,2x+3与-5x+6互为相反数?
2x+3=-(-5x+6)
移项得, 2x-5x=-6-3
合并同类项得, -3x=-9
系数化为1得, x=
课堂测试
3.若 与 是同类项,则m,n的值分别为( )
A.2,-1 B.-2,1 C.-1,2 D.-2,-1
分析:因为 与 是同类项,所以可得方程 和 .解可得m=2;解 可得n=-1.故答案为A.
课堂测试
4.解下列方程:
(1) 16x-40=9x-16
(2) xx-3
(3) 3x+1=0.9x+7
(4) 3y+9-2y+2=10-4y
课堂测试
5.(1)已知x=2是关于x的方程a(x+1)=0.5a+x的解,则a的值为多少?
(2)当x=2时,式子a(x+1)与式子0.5a+x的值相同,则a的值为多少?
(3)已知关于x的方程a(x+1)=0.5a+x的解与方程4x+2=12-x的解相同,则a的值为多少?
提示:
1)将x=2带入到方程中求出a值
2)将x=2带入到方程中求出a值
3)先求后一个方程的解,再将所求的解带入到第一个方程中求a值。
探索提高
谢谢!
解一元一次方程(合并同类项-移项)
第三单元 一元一次方程
导入新课
讲授新课
当堂练习
课堂小结
初中数学
七年级 上册
例:将下列各式合并同类项
解:(1)
(2)
(3)
5
同类项
所含字母相同
相同字母的指数也相同
合并同类项
字母部分不变
系数相加减
合并同类项知识点回顾
前年购买量+去年购买量+今年购买量=140台
x + 2 x + 4 x =140
分析:
2.数量关系:
4.转化为方程:
3.相等关系:
问题:某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
1 .设未知数:
前年购买台数 去年购买台数 今年购买台数
x
2x
4x
“各部分量的和=总量”是一个基本的相等关系
思考
问题:某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
设前年购买电脑台数为x台
x+2x+4x=140
分析:解方程,就是把方程变形为 x = a(a为常数)的形式.
合并同类项
7x=140
系数化为1(利用等式的基本性质2,方程左右两边同时除以7)
x=20
思考
上面解方程中“合并同类项起了什么作用?
合并同类项起到了“ 化简”的作用,
把含有未知数的项合并为一项,
从而把方程转化为ax=b,
使其更接近x=a的形式
(其中a,b是常数) .
思考
例1:解下列方程
解:
解:
(等式两边同时除以-3)
(等式两边同时乘以-2)
思考
例2:三个连续整数的和等于27,求这三个数。
设第一个数为x,则第二个数为x+1,第三个数为x+2
x+x+1+x+2=27
合并同类项
等式的性质1
3x+3=27
3x+3-3=27-3
系数化为1
x=8
则这三个数分别是8、9、10
思考
列方程解应用题分哪些步骤?
①审:审清题意
②设:设出合理的未知数
③找:找出相等关系
④列:列出方程
⑤解:求出方程的解
⑦答:作答
⑥验:检验答案是否正确
小结
解下列方程
(2)
(1)
(3)
课堂测试
一个足球的表面一共有32个皮块,黑色与白色皮块的数目比为3:5,你能求出黑色皮块和白色皮块各有多少吗?
解:设黑色皮块有3x个,
则白色皮块有5x个,
依题意,得
分析:黑色皮块+白色皮块=32个皮块
3x+5x=32
合并同类项,得
8x=32
x=4
系数化为1,得
答:黑色皮块有12个,白色皮块有20个。
3x=12
5x=20
所以
课堂测试
太阳下山晚霞红,我把鸭子赶回笼;一半在外闹哄哄,一半的一半进笼中;剩下十五围着我,请算多少帮我忙。你能列出方程来解决这个问题吗?
解:设有鸭子x只
探索提高
把一些图书分给七(3)班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
分析:
设这个班有x名学生.
每人分3本,还剩余20本,则这批书共 本;
每人分4本,还缺25本,则这批书共 本;
(3x+20)
(4x-25)
3x+20=4x-25
(4)根据题意可列方程为________________________
因为这批书的总数是一个定值,
表示它的两个式子应相等
等式左右两边都有未知数,
如何求得方程的解呢?
思 考
如何求方程3x+20=4x-25的解?
把它变成x=a(常数)的形式
3x+20 = 4x-25
等式两边都含有
x的项和不含字母的常数项。
利用等式性质1,将等式
变为x=a(常数)的形式
3x+20-4x-20=4x-25-4x-20
3x-4x=-25-20
-x=-45
合并同类项
x=45
思 考
3x+20 = 4x-25
3x-4x = -25-20
下面方程的变形,把某项从等式的一边移动到另一边时有什么变化?
把等式一边的某项变号后移到另一边,叫做移项.
符号发生变化
移项的依据:
等式的性质1
观察
判断下面的移项是否正确?
(1) 10+x=10 移项,得 x=10+10
(2) 3x=x-5 移项,得 3x+x=-5
(3) 3x=6-2x 移项,得 3x+2x=-6
(4) 1-2x=-3x 移项,得 3x-2x=-1
(5) 2x+8=12-6x 移项,得 2x+6x=12-8
知识巩固
上述解方程中“ 移项”起了什么作用?
解方程时经常要“ 合并同类项”和“移项”,已达到化简的目的。
思 考
(1)3x+7=32-2x
解:
移项得:
3x+2x=32-7
合并同类项,得
5x=25
系数化为1,得
x=5
解:
移项,得:
合并同类项,得:
系数化为1,得
x=-8
解方程时注意移项后
符号发生变化
解方程
1.小亮在计算 41-N 时,误将“ -”看成“ +”,结果得13,则41-N的值应为( )
A.-28 B.54 C.69 D.-54
根据题意,41+N=13,
移项后解得N=-28,
∴41-N=41-(-28)=69.
故选C.
课堂测试
2.(1)当x取何值时,2x+3与-5x+6相等?
2x+3=-5x+6
移项得, 2x+5x= 6-3
合并同类项得, 7x=3
系数化为1得, x=
(2)当x取何值时,2x+3与-5x+6互为相反数?
2x+3=-(-5x+6)
移项得, 2x-5x=-6-3
合并同类项得, -3x=-9
系数化为1得, x=
课堂测试
3.若 与 是同类项,则m,n的值分别为( )
A.2,-1 B.-2,1 C.-1,2 D.-2,-1
分析:因为 与 是同类项,所以可得方程 和 .解可得m=2;解 可得n=-1.故答案为A.
课堂测试
4.解下列方程:
(1) 16x-40=9x-16
(2) xx-3
(3) 3x+1=0.9x+7
(4) 3y+9-2y+2=10-4y
课堂测试
5.(1)已知x=2是关于x的方程a(x+1)=0.5a+x的解,则a的值为多少?
(2)当x=2时,式子a(x+1)与式子0.5a+x的值相同,则a的值为多少?
(3)已知关于x的方程a(x+1)=0.5a+x的解与方程4x+2=12-x的解相同,则a的值为多少?
提示:
1)将x=2带入到方程中求出a值
2)将x=2带入到方程中求出a值
3)先求后一个方程的解,再将所求的解带入到第一个方程中求a值。
探索提高
谢谢!
