2022—2023学年人教版数学七年级上册 3.4 实际问题与一元一次方程 课件 (共21张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学七年级上册 3.4 实际问题与一元一次方程 课件 (共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 06:54:43 | ||
图片预览





文档简介
(共21张PPT)
3.4 实际问题与一元一次方程
1、一件衣服标价为 元,商场打 折销售,则衣服
的售价是 元。
2、一个篮球实际进价为 元,商场以 元
销售,则商场卖一个篮球可获利 元,
利润率是
3、一双运动鞋进价 元,将它提价 后标价,则标价
应是 元。
9
100
a
a
b (b>a)
x%
(b-a)
100(1+x%)
0.9a
热身 运动
利润 = 售价-进价
打 x 折的售价=
原价×
售价 = 进价+利润=进价×(1+利润率)
利润率 =
进价
利润
×100%
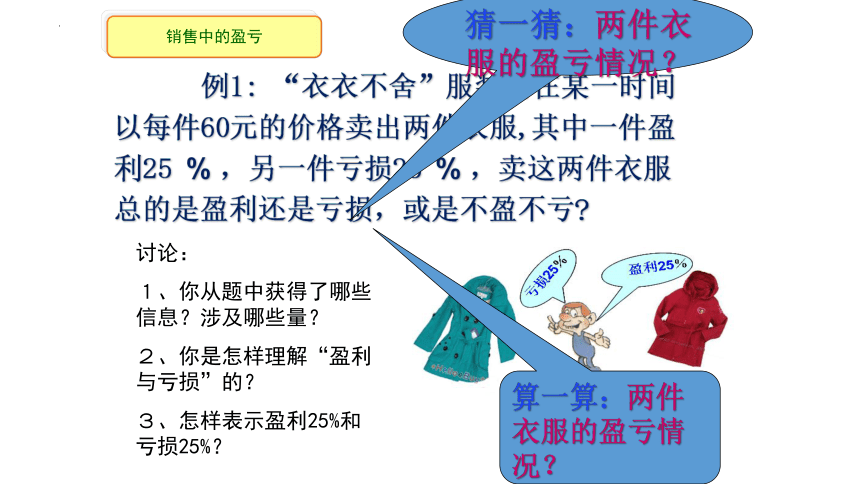
例1: “衣衣不舍”服装店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25 % ,另一件亏损25 % ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏
猜一猜:两件衣服的盈亏情况?
讨论:
1、你从题中获得了哪些信息?涉及哪些量?
2、你是怎样理解“盈利 与亏损”的?
3、怎样表示盈利25%和亏损25%?
算一算:两件衣服的盈亏情况?
销售中的盈亏
算一算
售价 进价
0.25x
利润
盈利20%
60
x
亏损20%
y
60
-0.25y
解:设盈利20%的衣服进价为 x 元,
根据题意可列方程
x + 0.25x = 60
解得 x = 48
亏损20%的衣服的进价为 y 元,
y - 0.25y = 60
y = 80
总进价为 x+y =
总售价为 120元
128元
因为 总进价 大于 总售价,
所以亏了8元.
方法构想
1
例1: “衣衣不舍”服装店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25 % ,另一件亏损25 % ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏
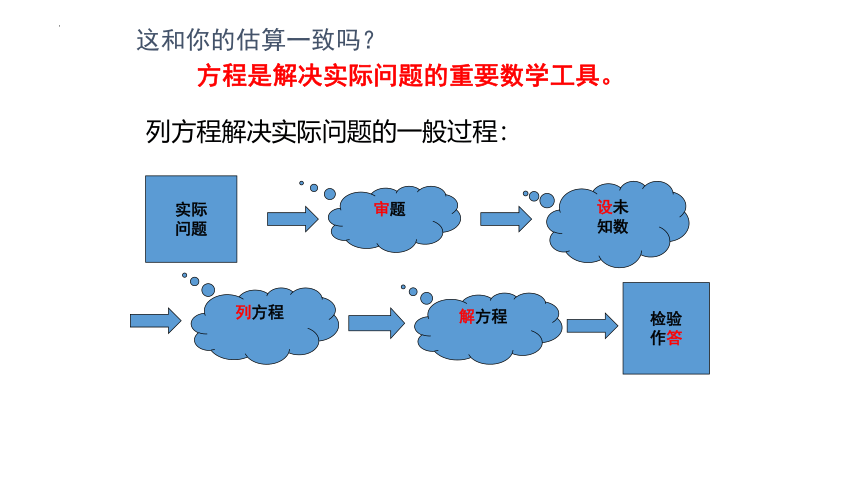
列方程解决实际问题的一般过程:
这和你的估算一致吗?
审题
实际
问题
设未
知数
列方程
解方程
检验
作答
方程是解决实际问题的重要数学工具。
进价、售价、利润、利润率
记住了
?
理性提升
上述问题中涉及到哪些量?
●售价、进价、利润的关系式:
= 商品售价—商品进价
商品利润
●进价、利润、利润率的关系:
利润率=
商品进价
商品利润
×100%
●标价、折扣数、商品售价关系 :
商品售价=
标价×
折扣数
10
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
关系式:
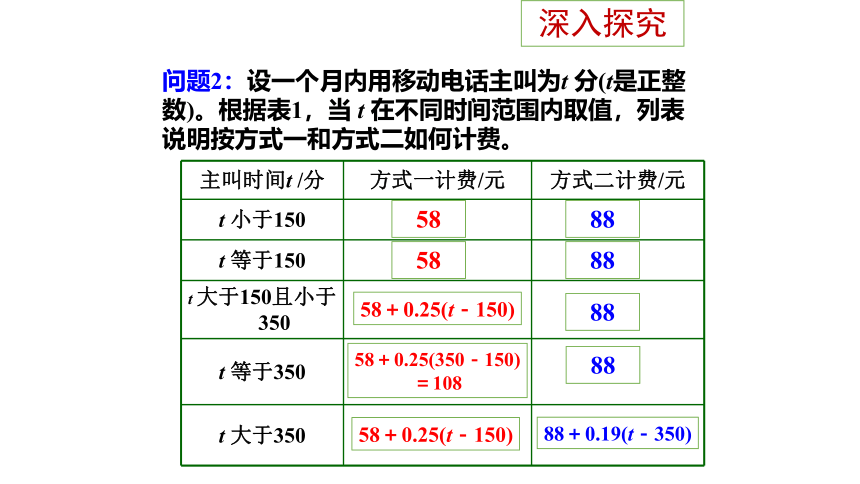
问题2:设一个月内用移动电话主叫为t 分(t是正整数)。根据表1,当 t 在不同时间范围内取值,列表说明按方式一和方式二如何计费。
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
深入探究
58
88
58
88
58+0.25(t-150)
88
88
58+0.25(350-150)=108
58+0.25(t-150)
88+0.19(t-350)
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
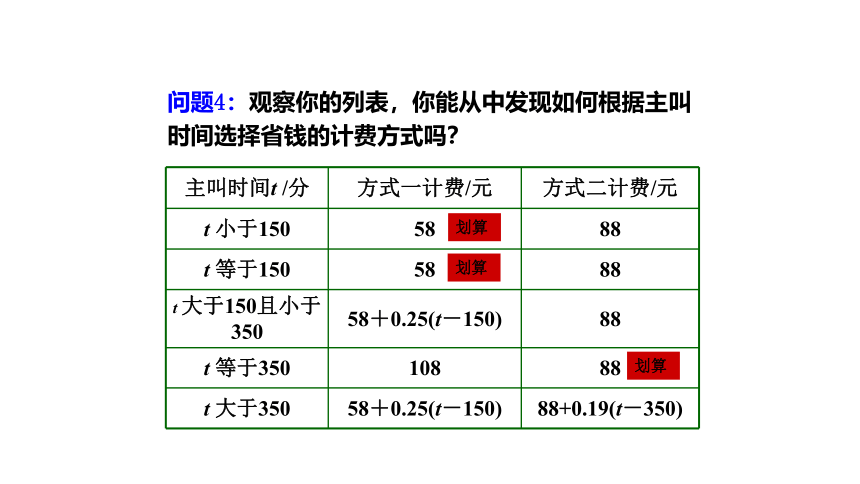
问题4:观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
划算
划算
划算
主叫时间t /分 方式一计费/元 方式二计费/元
t大于150且小于 350 58+0.25(t-150) 88
依题意得: 58+0.25(t-150) = 88
去括号得: 58+0.25t-37.5 = 88
移项、合并同类项得: 0.25t = 67.5
系数化1得: t = 270
∴当 t =270分时,两种计费方式的费用相等。
那么当150< t <270分和270< t <350时,两种计费方式哪种更合算呢?
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于350 58+0.25(t-150) 88+0.19(t-350)
当t >350分时,两种计费方式哪种更合算呢?
问题5:综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱。
0
计费方式一
计费方式二
270
t 小于 270分
t 大于 270分
请回顾电话计费问题的探究过程,并回答以下问题:
(1)电话计费问题的核心问题是什么?
(2)探究解题的过程大致包含哪几个步骤?
(3)我们在探究过程中用到了哪些方法,你有哪些收获?
归纳小结
利用我们在“电话计费问题”中学会的方法,探究下面的问题:
用A4纸在某誊印社复印文件,复印页数不超过20时每页收费0.12元;复印页数超过20页时,超过部分每页收费0.09元。在某图书馆复印同样的文件,不论复印多少页,每页收费0.1元。 如何根据复印的页数选择复印的地点使总价格比较便宜?(复印的页数不为零)
巩固应用
复印页数x 誊印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:依题意列表得:
(1)当 x 小于20时,0.12 x大于0.1 x恒成立,图书馆价格便宜;
(2)当 x 等于20时,2.4大于2,图书馆价格便宜;
(3)当 x 大于20时,
依题意得:2.4+0.09(x-20)=0.1x
解得: x=60
∴ 当x大于20且小于60时,图书馆价格便宜;
当x大于60时,誊印社价格便宜。
综上所述:当x小于60页时,图书馆价格便宜;
当x大于60时,誊印社价格便宜。
小明想用一根长为12米的铁丝围成一个长方形.
(1)使得这个长方形的长比宽多1.4米,此时长方形的长、宽各为多少米?
例题讲解(3)
解:设此时长方形的宽为x米,
2(x+x+1.4)=12
4x=9.2
x=2.3
长方形的长为2.3+1.4=3.7
∴长方形的长为3.7米,宽为2.3米
则它的长为(x+1.4)米,
根据题意,得
长=宽+1.4
2(长+宽)=12
(2)使得长方形的长比宽多一倍,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围成的长方形相比、面积有什么变化?
解:设此时长方形的宽为x米,
2(x+2x)=12
x=2
长方形的长2x =4
则它的长为2x米,
根据题意,得
∴长方形的长为4米,宽为2米,
S=4×2=8米2,
(1)中的长方形围成的面积:3.7×2.3=8.51米2
比(1)中面积减少了8.51-8=0.51米2
2x
例题讲解(2)
小明想用一根长为12米的铁丝围成一个长方形.
周长相等的长方形面积不定
长=宽+宽
2(长+宽)=12
(3)使得围成一个正方形,此时正方形的边长是多少米?它所围成的面积与(2)中相比又有什么变化?
解:设此时正方形的边长为x米,根据题意,得
4x=12
x=3
比(2)中面积增大8-8=1 米2
X
正方形的边长为3米,
S=3×3=9米2
同样长的铁丝围成怎样的四边形面积最大呢?
例题讲解(3)
小明想用一根长为12米的铁丝围成一个长方形.
长=宽
4=12
面积: 3.7×2.3= 8.51
面积:
2 ×4=8
面积:
3 ×3=9
围成正方形时四边形面积最大
小结
(4)在墙边围成一个菜地,使长比宽大4米,问小明围成的菜地的长和宽各是多少呢?(墙面足够长)
例题讲解(4)
小明想用一根长为12米的铁丝围成一个长方形.
铁丝
墙面
x
x+4
解:设此时长方形的宽为x米,
2(2x+x+4)=12
则它的长为(x+4)米,
根据题意,得
长=宽+4
2宽+长=12
用一元一次方程解决实际问题的基本过程和步骤:
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题的答案
检 验
关键:找出等量关系,将实际问题抽象为方程这一数学模型
归纳总结
审
设
列
解
答
验
3.4 实际问题与一元一次方程
1、一件衣服标价为 元,商场打 折销售,则衣服
的售价是 元。
2、一个篮球实际进价为 元,商场以 元
销售,则商场卖一个篮球可获利 元,
利润率是
3、一双运动鞋进价 元,将它提价 后标价,则标价
应是 元。
9
100
a
a
b (b>a)
x%
(b-a)
100(1+x%)
0.9a
热身 运动
利润 = 售价-进价
打 x 折的售价=
原价×
售价 = 进价+利润=进价×(1+利润率)
利润率 =
进价
利润
×100%
例1: “衣衣不舍”服装店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25 % ,另一件亏损25 % ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏
猜一猜:两件衣服的盈亏情况?
讨论:
1、你从题中获得了哪些信息?涉及哪些量?
2、你是怎样理解“盈利 与亏损”的?
3、怎样表示盈利25%和亏损25%?
算一算:两件衣服的盈亏情况?
销售中的盈亏
算一算
售价 进价
0.25x
利润
盈利20%
60
x
亏损20%
y
60
-0.25y
解:设盈利20%的衣服进价为 x 元,
根据题意可列方程
x + 0.25x = 60
解得 x = 48
亏损20%的衣服的进价为 y 元,
y - 0.25y = 60
y = 80
总进价为 x+y =
总售价为 120元
128元
因为 总进价 大于 总售价,
所以亏了8元.
方法构想
1
例1: “衣衣不舍”服装店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25 % ,另一件亏损25 % ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏
列方程解决实际问题的一般过程:
这和你的估算一致吗?
审题
实际
问题
设未
知数
列方程
解方程
检验
作答
方程是解决实际问题的重要数学工具。
进价、售价、利润、利润率
记住了
?
理性提升
上述问题中涉及到哪些量?
●售价、进价、利润的关系式:
= 商品售价—商品进价
商品利润
●进价、利润、利润率的关系:
利润率=
商品进价
商品利润
×100%
●标价、折扣数、商品售价关系 :
商品售价=
标价×
折扣数
10
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
关系式:
问题2:设一个月内用移动电话主叫为t 分(t是正整数)。根据表1,当 t 在不同时间范围内取值,列表说明按方式一和方式二如何计费。
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
深入探究
58
88
58
88
58+0.25(t-150)
88
88
58+0.25(350-150)=108
58+0.25(t-150)
88+0.19(t-350)
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
问题4:观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
划算
划算
划算
主叫时间t /分 方式一计费/元 方式二计费/元
t大于150且小于 350 58+0.25(t-150) 88
依题意得: 58+0.25(t-150) = 88
去括号得: 58+0.25t-37.5 = 88
移项、合并同类项得: 0.25t = 67.5
系数化1得: t = 270
∴当 t =270分时,两种计费方式的费用相等。
那么当150< t <270分和270< t <350时,两种计费方式哪种更合算呢?
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于350 58+0.25(t-150) 88+0.19(t-350)
当t >350分时,两种计费方式哪种更合算呢?
问题5:综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱。
0
计费方式一
计费方式二
270
t 小于 270分
t 大于 270分
请回顾电话计费问题的探究过程,并回答以下问题:
(1)电话计费问题的核心问题是什么?
(2)探究解题的过程大致包含哪几个步骤?
(3)我们在探究过程中用到了哪些方法,你有哪些收获?
归纳小结
利用我们在“电话计费问题”中学会的方法,探究下面的问题:
用A4纸在某誊印社复印文件,复印页数不超过20时每页收费0.12元;复印页数超过20页时,超过部分每页收费0.09元。在某图书馆复印同样的文件,不论复印多少页,每页收费0.1元。 如何根据复印的页数选择复印的地点使总价格比较便宜?(复印的页数不为零)
巩固应用
复印页数x 誊印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:依题意列表得:
(1)当 x 小于20时,0.12 x大于0.1 x恒成立,图书馆价格便宜;
(2)当 x 等于20时,2.4大于2,图书馆价格便宜;
(3)当 x 大于20时,
依题意得:2.4+0.09(x-20)=0.1x
解得: x=60
∴ 当x大于20且小于60时,图书馆价格便宜;
当x大于60时,誊印社价格便宜。
综上所述:当x小于60页时,图书馆价格便宜;
当x大于60时,誊印社价格便宜。
小明想用一根长为12米的铁丝围成一个长方形.
(1)使得这个长方形的长比宽多1.4米,此时长方形的长、宽各为多少米?
例题讲解(3)
解:设此时长方形的宽为x米,
2(x+x+1.4)=12
4x=9.2
x=2.3
长方形的长为2.3+1.4=3.7
∴长方形的长为3.7米,宽为2.3米
则它的长为(x+1.4)米,
根据题意,得
长=宽+1.4
2(长+宽)=12
(2)使得长方形的长比宽多一倍,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围成的长方形相比、面积有什么变化?
解:设此时长方形的宽为x米,
2(x+2x)=12
x=2
长方形的长2x =4
则它的长为2x米,
根据题意,得
∴长方形的长为4米,宽为2米,
S=4×2=8米2,
(1)中的长方形围成的面积:3.7×2.3=8.51米2
比(1)中面积减少了8.51-8=0.51米2
2x
例题讲解(2)
小明想用一根长为12米的铁丝围成一个长方形.
周长相等的长方形面积不定
长=宽+宽
2(长+宽)=12
(3)使得围成一个正方形,此时正方形的边长是多少米?它所围成的面积与(2)中相比又有什么变化?
解:设此时正方形的边长为x米,根据题意,得
4x=12
x=3
比(2)中面积增大8-8=1 米2
X
正方形的边长为3米,
S=3×3=9米2
同样长的铁丝围成怎样的四边形面积最大呢?
例题讲解(3)
小明想用一根长为12米的铁丝围成一个长方形.
长=宽
4=12
面积: 3.7×2.3= 8.51
面积:
2 ×4=8
面积:
3 ×3=9
围成正方形时四边形面积最大
小结
(4)在墙边围成一个菜地,使长比宽大4米,问小明围成的菜地的长和宽各是多少呢?(墙面足够长)
例题讲解(4)
小明想用一根长为12米的铁丝围成一个长方形.
铁丝
墙面
x
x+4
解:设此时长方形的宽为x米,
2(2x+x+4)=12
则它的长为(x+4)米,
根据题意,得
长=宽+4
2宽+长=12
用一元一次方程解决实际问题的基本过程和步骤:
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x = a)
实际问题的答案
检 验
关键:找出等量关系,将实际问题抽象为方程这一数学模型
归纳总结
审
设
列
解
答
验
