2022—2023学年人教版数学八年级上册 11.3.2 多边形的内角和 课件(共17张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册 11.3.2 多边形的内角和 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 06:59:23 | ||
图片预览


文档简介
(共17张PPT)
多边形的内角和
知识回顾
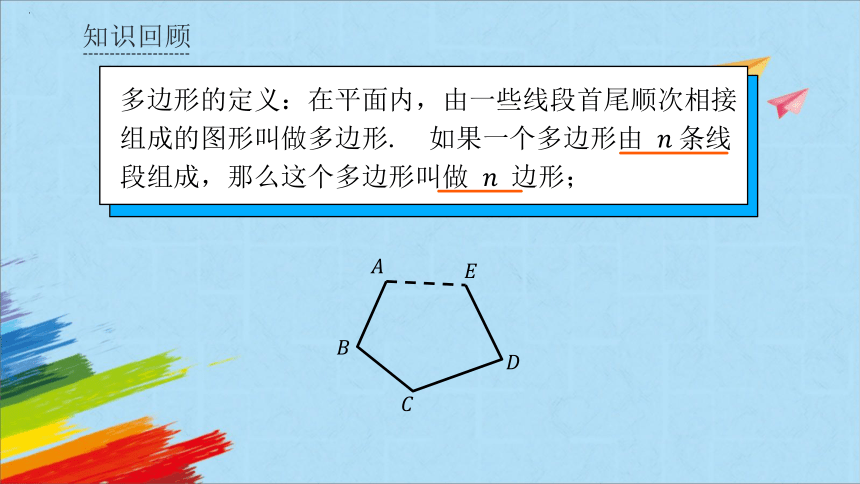
多边形的定义:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形. 如果一个多边形由 条线段组成,那么这个多边形叫做 边形;
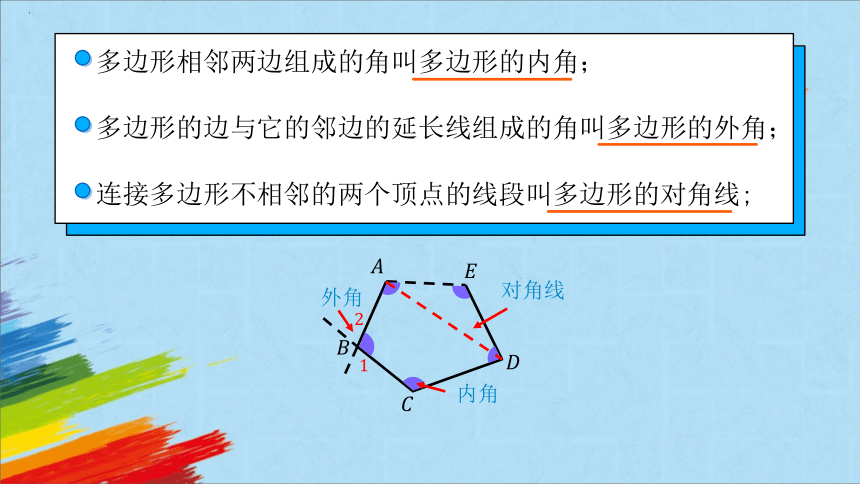
多边形相邻两边组成的角叫多边形的内角;
多边形的边与它的邻边的延长线组成的角叫多边形的外角;
连接多边形不相邻的两个顶点的线段叫多边形的对角线;
外角
内角
对角线
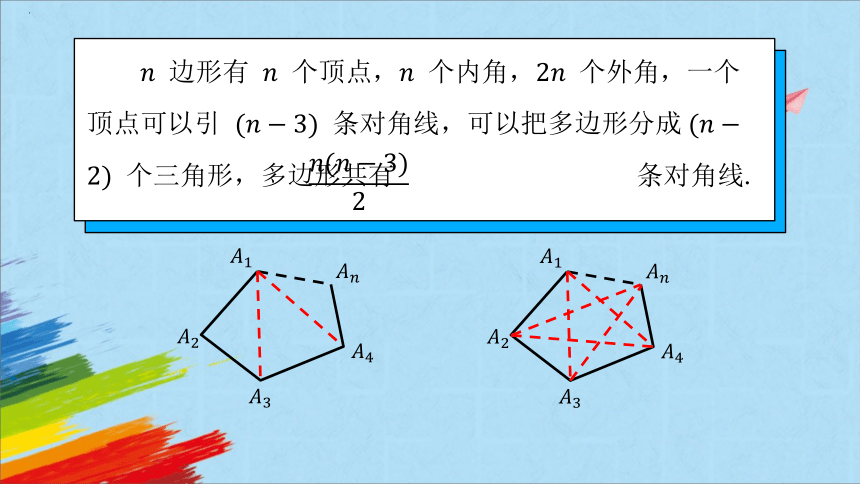
边形有 个顶点, 个内角, 个外角,一个顶点可以引 条对角线,可以把多边形分成 个三角形,多边形共有 条对角线.
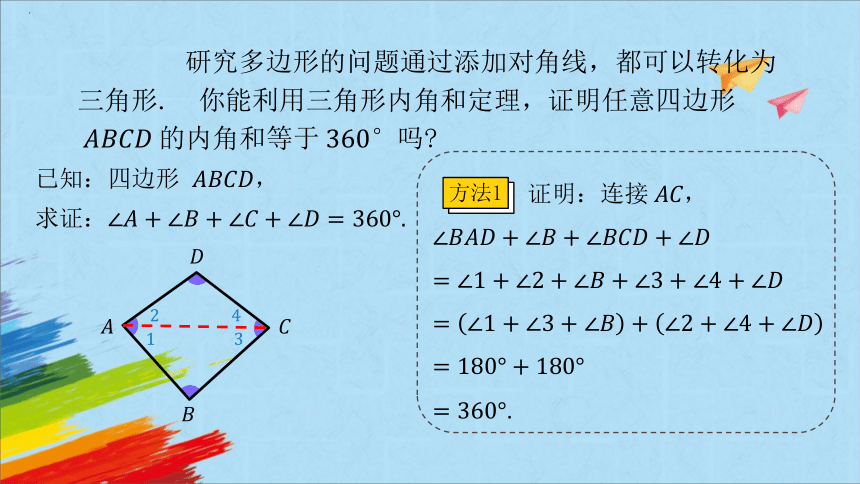
研究多边形的问题通过添加对角线,都可以转化为三角形. 你能利用三角形内角和定理,证明任意四边形的内角和等于吗
已知:四边形
求证:
方法1
证明:连接,
.
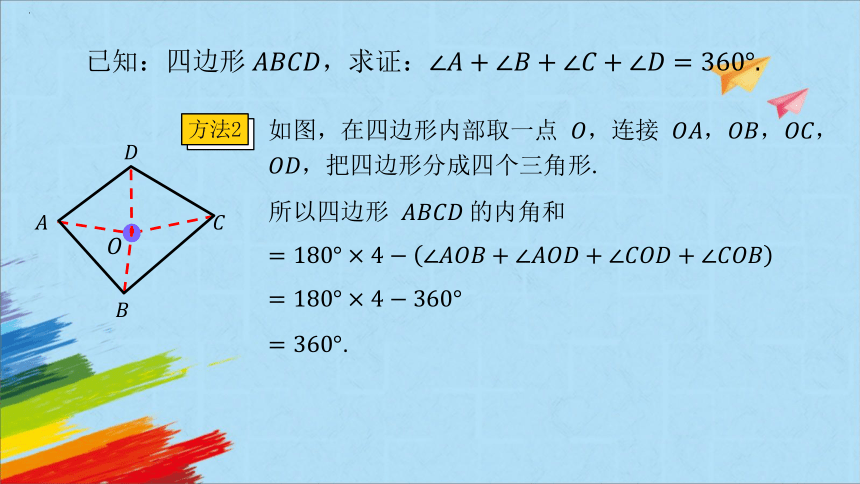
已知:四边形,求证:
方法2
如图,在四边形内部取一点 ,连接 ,,,,把四边形分成四个三角形.
所以四边形 的内角和
.
方法3
如图,在 边上取一点 ,连接,,把四边形分成三个三角形.
所以四边形 的内角和
.
已知:四边形,求证:
方法4
如图,在四边形外任取一点,连接,, , ,把四边形转化为有一个公共顶点的三个三角形.
.
已知:四边形,求证:
所以四边形 的内角和
四边形可以如此解决,多边形的问题也可以通过添加辅助线转化成三角形问题来解决.
以上这四种方法都运用了转化的思想,把四边形分割成三角形,转化为已学的三角形内角和进行求解.
图一
图二
图三
图四
多边形内角和公式为
多边形的问题可以转化为三角形的问题来研究,将未知转化为已知.
多边形的内角和仅与边数有关,与多边形的大小无关.
八边形的内角和是 ;
十边形的内角和是 .
小结
根据题意画图,在四边形 中
例
如果一个四边形的一组对角互补,那么另一组对角有什么关系
.
.
如果一个四边形的一组对角互补,那么另一组对角也互补.
例
如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少
因为六边形的任何一个外角加上与它相邻的内角都等于,因此六边形的 个外角加上它们相邻的内角,所得的总和等于 .
所以外角和为
一个多边形的内角和是,它是 边形.
根据多边形的内角和公式,可得
解方程得 ,所以是十一边形.
十一
一个多边形的每一个外角都等于 ,则这个多边形为 边形.
由每一个外角都等于 ,多边形的外角和为,用除以 可得这个多边形是十二边形.
十二
一个多边形的内角和与外角和相等,它是几边形
由多边形的内角和与外角和相等,
可得方程为 ,解得 ,
所以多边形的内角和与外角和相等是四边形.
问题
课
堂
小
结
把多边形的问题可以转化为三角形的问题来研究,将未知转化为已知.
多边形的内角和为 ,内角和仅与边数有关,与多边形的大小无关,边数每增加,内角和增加.
多边形的外角和为,不随边数的改变而改变.
1
2
3
布置作业
,,,.
多边形的内角和
知识回顾
多边形的定义:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形. 如果一个多边形由 条线段组成,那么这个多边形叫做 边形;
多边形相邻两边组成的角叫多边形的内角;
多边形的边与它的邻边的延长线组成的角叫多边形的外角;
连接多边形不相邻的两个顶点的线段叫多边形的对角线;
外角
内角
对角线
边形有 个顶点, 个内角, 个外角,一个顶点可以引 条对角线,可以把多边形分成 个三角形,多边形共有 条对角线.
研究多边形的问题通过添加对角线,都可以转化为三角形. 你能利用三角形内角和定理,证明任意四边形的内角和等于吗
已知:四边形
求证:
方法1
证明:连接,
.
已知:四边形,求证:
方法2
如图,在四边形内部取一点 ,连接 ,,,,把四边形分成四个三角形.
所以四边形 的内角和
.
方法3
如图,在 边上取一点 ,连接,,把四边形分成三个三角形.
所以四边形 的内角和
.
已知:四边形,求证:
方法4
如图,在四边形外任取一点,连接,, , ,把四边形转化为有一个公共顶点的三个三角形.
.
已知:四边形,求证:
所以四边形 的内角和
四边形可以如此解决,多边形的问题也可以通过添加辅助线转化成三角形问题来解决.
以上这四种方法都运用了转化的思想,把四边形分割成三角形,转化为已学的三角形内角和进行求解.
图一
图二
图三
图四
多边形内角和公式为
多边形的问题可以转化为三角形的问题来研究,将未知转化为已知.
多边形的内角和仅与边数有关,与多边形的大小无关.
八边形的内角和是 ;
十边形的内角和是 .
小结
根据题意画图,在四边形 中
例
如果一个四边形的一组对角互补,那么另一组对角有什么关系
.
.
如果一个四边形的一组对角互补,那么另一组对角也互补.
例
如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少
因为六边形的任何一个外角加上与它相邻的内角都等于,因此六边形的 个外角加上它们相邻的内角,所得的总和等于 .
所以外角和为
一个多边形的内角和是,它是 边形.
根据多边形的内角和公式,可得
解方程得 ,所以是十一边形.
十一
一个多边形的每一个外角都等于 ,则这个多边形为 边形.
由每一个外角都等于 ,多边形的外角和为,用除以 可得这个多边形是十二边形.
十二
一个多边形的内角和与外角和相等,它是几边形
由多边形的内角和与外角和相等,
可得方程为 ,解得 ,
所以多边形的内角和与外角和相等是四边形.
问题
课
堂
小
结
把多边形的问题可以转化为三角形的问题来研究,将未知转化为已知.
多边形的内角和为 ,内角和仅与边数有关,与多边形的大小无关,边数每增加,内角和增加.
多边形的外角和为,不随边数的改变而改变.
1
2
3
布置作业
,,,.
