2022—2023学年人教版数学八年级上册 11.3.2多边形的内角和 课件(共17张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册 11.3.2多边形的内角和 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 07:01:33 | ||
图片预览



文档简介
(共17张PPT)
11.3.2多边形的内角和
旧知回顾
1、多边形是如何定义的?
2、什么是正多边形?
在平面内,由若干条不在同一直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
在平面内,每个内角都相等、每条边也都相等的多边形叫做正多边形。
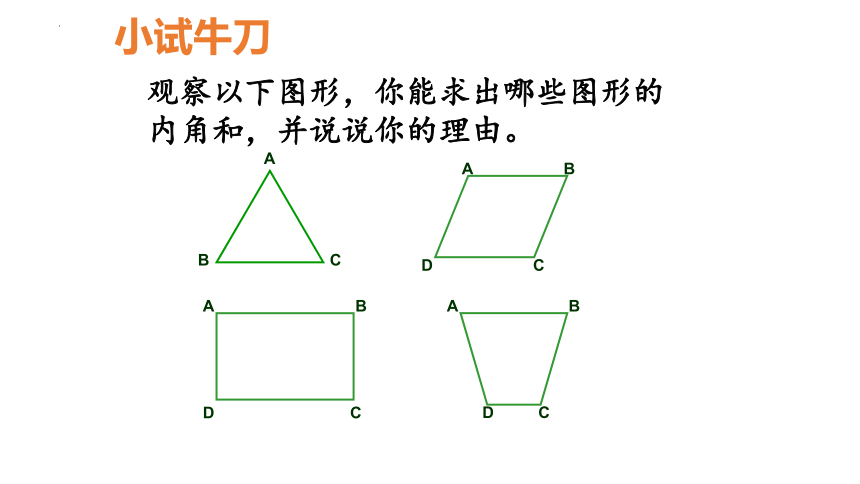
小试牛刀
观察以下图形,你能求出哪些图形的内角和,并说说你的理由。
A
B
C
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
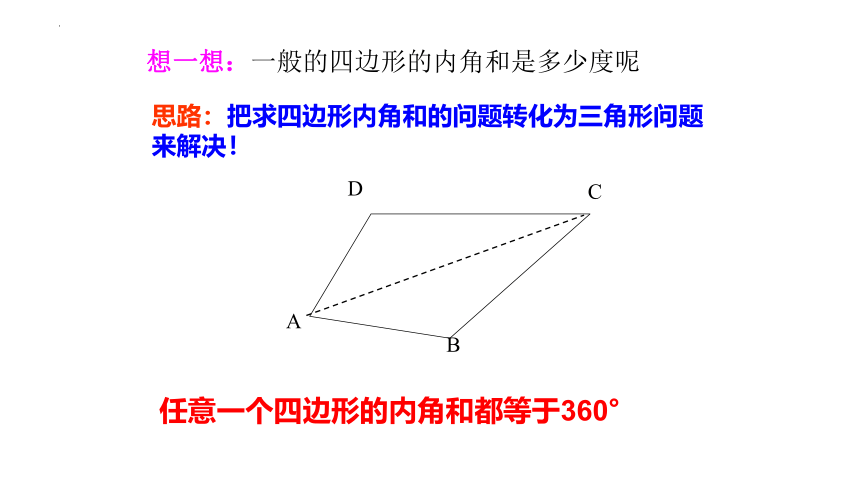
任意一个四边形的内角和都等于360°
思路:把求四边形内角和的问题转化为三角形问题来解决!
想一想:一般的四边形的内角和是多少度呢
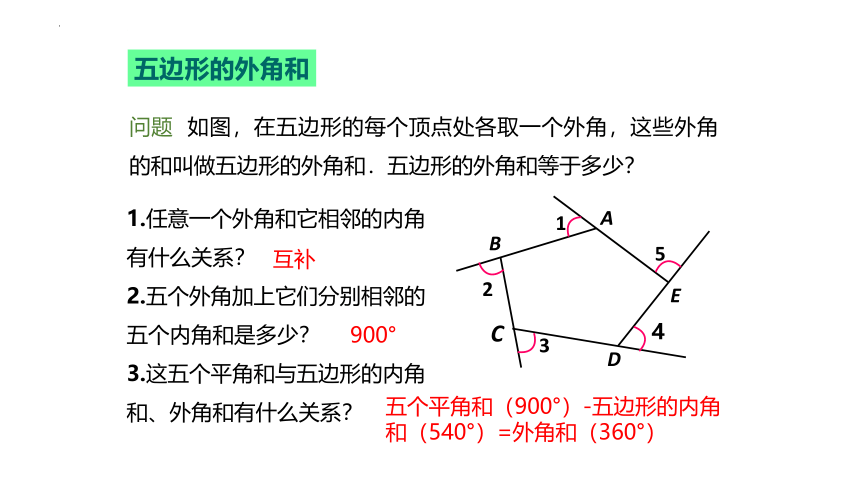
五边形的外角和
问题 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
互补
900°
五个平角和(900°)-五边形的内角和(540°)=外角和(360°)
E
B
C
D
1
2
3
4
5
A
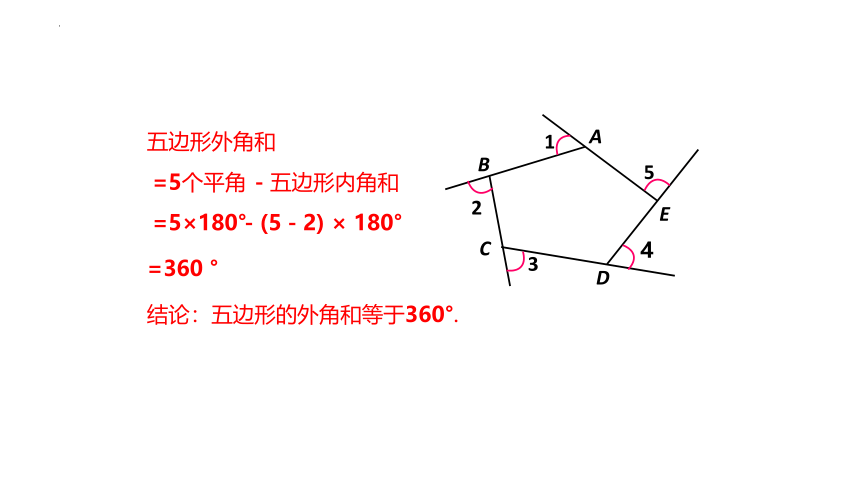
五边形外角和
=360 °
=5个平角
-五边形内角和
=5×180°
-(5-2) × 180°
结论:五边形的外角和等于360°.
根据四五边形的内角和的求法,你能否求出、六边形、七边形以及n边形的内角和?试试看,并与同伴交流,把结果汇报在下面表格中。
多边形 边数 一个顶点出发的对角线条数 图形 分成三角形的个数 计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
0
n-3
1
2
3
4
1
2
3
4
5
n-2
(n-2) ·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
应用多边形的内角和公式解决下列问题
1.十边形的内角和为多少度?
2.已知一个多边形的内角和为1 080°,则它的边数
为多少?
3.求出下列图形中x的值.
x°
x°
140°
1.十边形的内角和为多少度?
所以十边形的内角和等于
解:因为n边形的内角和公式为(n -2)×180°
2.已知一个多边形的内角和为1 080°,则它的边数为多少?
解:设该多边形的边数为 n
根据多边形的内角和公式
可知
解得
则这个多边形的边数为8.
3,若一个多边形增加一条边,则它的内角和( )
A.增加180° B.减少360°
C.不变 D.增加360 °
A
巩固练习
1.判断.
(1)当多边形边数增加时,它的内角和也随着增加.( )
(2)当多边形边数增加时,它的外角和也随着增加.( )
(3)三角形的外角和与八边形的外角和相等. ( )
2.一个正多边形的内角和为720°,则这个正多边形的
每一个内角等于______.
120°
3.一个多边形的内角和不可能是( )
A.1800° B.540 ° C.720 ° D.810 °
D
比一比
4、 如图:我国的国旗上的五星是正五角星,正五角星中的五边形ABCDE是正五边形,你能求出五角星中∠F的度数?
D
C
B
E
A
F
所以∠F=36°( )
所以∠BAE_____∠DEA
=108°
所以∠FAE=180°___∠BAE =72°,
∠FEA=180°____∠DEA =72°
解:因为五边形是
正五边形
=
—
—
三角形内角和180°
比一比
5.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n-2) 180°,
多边形外角和等于360°,
∴ (n-2) 180°=2× 360 .
解得 n=6.
∴这个多边形的边数为6.
多边形
内角和
内角和
(n-2) × 180 °(n ≥3的整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关.
正多边形
内角= ,外角=
11.3.2多边形的内角和
旧知回顾
1、多边形是如何定义的?
2、什么是正多边形?
在平面内,由若干条不在同一直线上的线段首尾顺次相连组成的封闭图形叫做多边形。
在平面内,每个内角都相等、每条边也都相等的多边形叫做正多边形。
小试牛刀
观察以下图形,你能求出哪些图形的内角和,并说说你的理由。
A
B
C
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
任意一个四边形的内角和都等于360°
思路:把求四边形内角和的问题转化为三角形问题来解决!
想一想:一般的四边形的内角和是多少度呢
五边形的外角和
问题 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
互补
900°
五个平角和(900°)-五边形的内角和(540°)=外角和(360°)
E
B
C
D
1
2
3
4
5
A
五边形外角和
=360 °
=5个平角
-五边形内角和
=5×180°
-(5-2) × 180°
结论:五边形的外角和等于360°.
根据四五边形的内角和的求法,你能否求出、六边形、七边形以及n边形的内角和?试试看,并与同伴交流,把结果汇报在下面表格中。
多边形 边数 一个顶点出发的对角线条数 图形 分成三角形的个数 计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
0
n-3
1
2
3
4
1
2
3
4
5
n-2
(n-2) ·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
应用多边形的内角和公式解决下列问题
1.十边形的内角和为多少度?
2.已知一个多边形的内角和为1 080°,则它的边数
为多少?
3.求出下列图形中x的值.
x°
x°
140°
1.十边形的内角和为多少度?
所以十边形的内角和等于
解:因为n边形的内角和公式为(n -2)×180°
2.已知一个多边形的内角和为1 080°,则它的边数为多少?
解:设该多边形的边数为 n
根据多边形的内角和公式
可知
解得
则这个多边形的边数为8.
3,若一个多边形增加一条边,则它的内角和( )
A.增加180° B.减少360°
C.不变 D.增加360 °
A
巩固练习
1.判断.
(1)当多边形边数增加时,它的内角和也随着增加.( )
(2)当多边形边数增加时,它的外角和也随着增加.( )
(3)三角形的外角和与八边形的外角和相等. ( )
2.一个正多边形的内角和为720°,则这个正多边形的
每一个内角等于______.
120°
3.一个多边形的内角和不可能是( )
A.1800° B.540 ° C.720 ° D.810 °
D
比一比
4、 如图:我国的国旗上的五星是正五角星,正五角星中的五边形ABCDE是正五边形,你能求出五角星中∠F的度数?
D
C
B
E
A
F
所以∠F=36°( )
所以∠BAE_____∠DEA
=108°
所以∠FAE=180°___∠BAE =72°,
∠FEA=180°____∠DEA =72°
解:因为五边形是
正五边形
=
—
—
三角形内角和180°
比一比
5.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.
解: 设多边形的边数为n.
∵它的内角和等于 (n-2) 180°,
多边形外角和等于360°,
∴ (n-2) 180°=2× 360 .
解得 n=6.
∴这个多边形的边数为6.
多边形
内角和
内角和
(n-2) × 180 °(n ≥3的整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关.
正多边形
内角= ,外角=
