2022-2023学年人教版八年级数学上册 12.1全等三角形 课件 (共23张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 12.1全等三角形 课件 (共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 07:06:45 | ||
图片预览





文档简介
(共23张PPT)
人教版八年级上册
12.1全等三角形
知识回顾
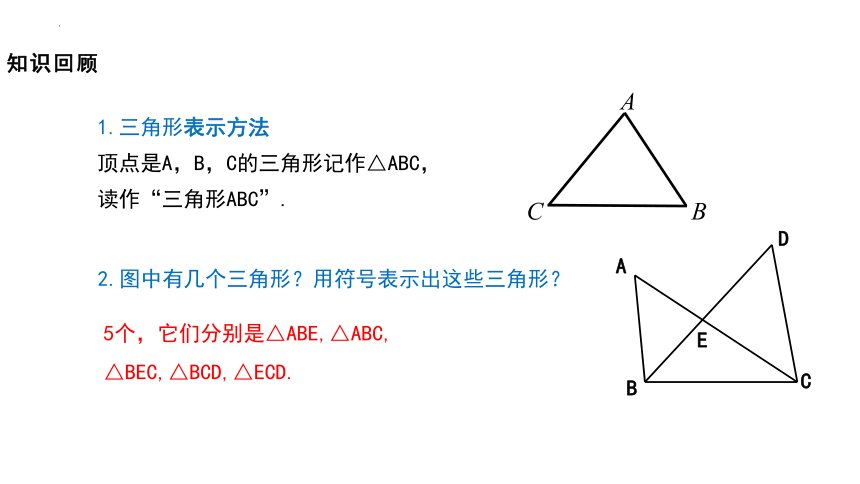
1.三角形表示方法
顶点是A,B,C的三角形记作△ABC,
读作“三角形ABC”.
A
B
C
2.图中有几个三角形?用符号表示出这些三角形?
A
B
C
D
E
5个,它们分别是△ABE,△ABC, △BEC,△BCD,△ECD.
教学目标
1. 熟记全等形及全等三角形的概念;能够正确找出全等三角形的对应边、对应角.
2. 熟练掌握全等三角形的性质,并能灵活运用全等三角形的性质解决相应的几何问题.
3. 初步帮助学生建立平移、翻折、旋转三种图形变化与全等形的关系.
新知导入
这是我们的天安门城楼,它建于明朝永乐十五年(1416年),设计者为明代御用建筑匠师蒯(kuǎi)祥,历经数百年依旧雄伟、神圣。
问题1:我们放大看看,在图中我们能不能找出形状、大小相同建筑结构或图案呢?
新知导入
问题2 我们可以看到天安门上有大量形状、大小相同的建筑结构和图案,在自然界也存在大量这种情况,你能找出下列图片中形状、大小相同的部分吗?
同层的花瓣
猫的耳朵、眼睛
新知导入
问题3 为验证这些图案的形状、大小都相同,请将下列图形变化方法与图片进行连线,使这些部分能够重合。
平移
翻折
旋转
新知探究
知识点 1
全等图形的定义及性质
可以看到通过平移、翻折、旋转,可以使这些形状、大小都相同的图形完全重合,在我们身边大量存在的这些全等图形,就是今天我们要探究的主角。
全等图形的定义
能够完全重合的两个图形叫做全等图形.
全等图形的性质
如果两个图形全等,它们的形状和大小一定都相等.
综上所述,在我们身边有大量全等图形,我们先从最基本的三角形开始学习
新知探究
全等三角形的有关概念和表示方法
知识点 2
E
D
F
A
B
C
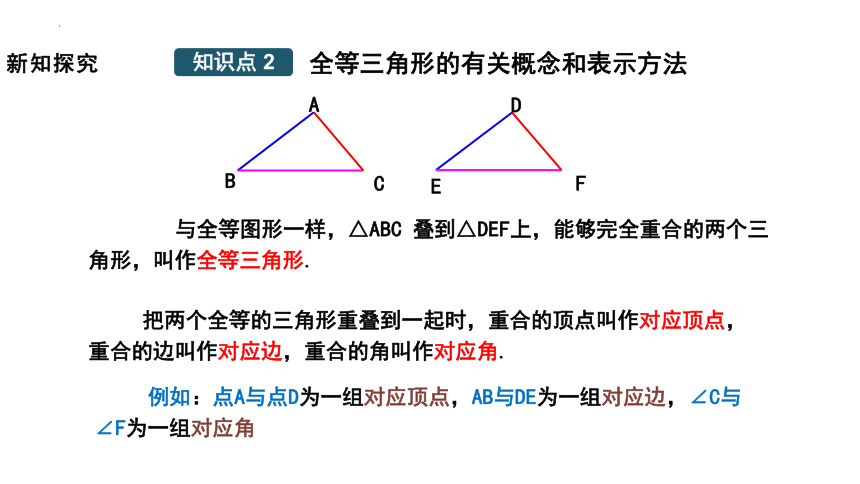
与全等图形一样,△ABC 叠到△DEF上,能够完全重合的两个三角形,叫作全等三角形.
把两个全等的三角形重叠到一起时,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角.
例如:点A与点D为一组对应顶点,AB与DE为一组对应边,∠C与∠F为一组对应角
新知探究
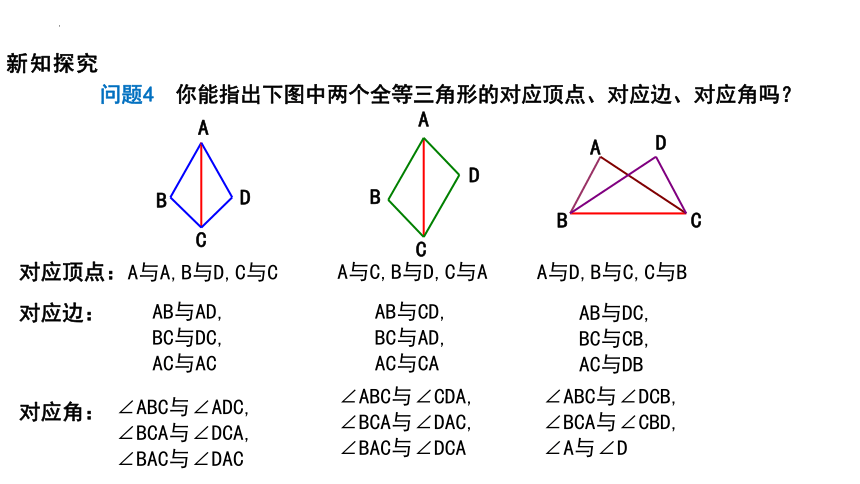
问题4 你能指出下图中两个全等三角形的对应顶点、对应边、对应角吗?
A
B
C
D
A
B
C
D
A
B
C
D
对应顶点:
对应边:
对应角:
A与A,B与D,C与C
AB与AD,
BC与DC,
AC与AC
∠ABC与∠ADC,
∠BCA与∠DCA,
∠BAC与∠DAC
A与C,B与D,C与A
AB与CD,
BC与AD,
AC与CA
∠ABC与∠CDA,
∠BCA与∠DAC,
∠BAC与∠DCA
A与D,B与C,C与B
AB与DC,
BC与CB,
AC与DB
∠ABC与∠DCB,
∠BCA与∠CBD,
∠A与∠D
新知探究
同时我们注意到,一个三角形通过平移、翻折、旋转后,所得到的三角形,能够与原来的三角形完全重合,所以我们将平移、翻折、旋转叫做全等变化。
即,一个图形经过平移、翻折、旋转后, 变化了,但 和 都没有改变,即平移、翻折、旋转前后的两个图形 .
形状
大小
全等
位置
A
B
C
G
E
F
A
C
B
D
A
B
C
D
新知探究
△ABC与△FDE全等,记作
△ABC≌△FDE
A
B
C
E
D
F
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
例如:
读作,△ABC全等于△FDE全等
注意:用“≌”记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
新知探究
全等三角形的性质
知识点 3
A
B
C
D
E
F
问题5 如图,△ABC≌△DEF,也就是两个三角形能够完全重合,你能找出相等的边和角吗?
相等的线段:AB=DE,AC=DF,BC=EF
相等的角:∠A=∠D,∠B=∠E,∠C=∠F
问题6 你有什么发现?
全等三角形的对应边相等,对应角相等。
新知小结
全等三角形的对应边相等,对应角相等
全等三角形的性质
∵△ABC≌△FDE,
∴A B=F D,A C=F E,B C=D E,(全等三角形对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E.(全等三角形对应角相等)
A
B
C
E
D
F
全等三角形的性质的几何语言
新知典例
A
D
F
C
E
B
1
2
A
B
D
C
1
4
2
3
E
A
B
C
F
1
2
例1 下图中红色与蓝色三角形全等,找出相等的线段和角?
A
B
C
D
F
相等的边
相等的角
AB=DE
BC=EF
AC=DF
BE=CF
∠B=∠1
∠2=∠F
∠A=∠D
AB=AF
BC=DF
AC=AD
BD=CF
∠B=∠F
∠BCA=∠ADC
∠BAC=∠DAF
∠BAD=∠FAC
AB=AE
BC=EF
AC=AF
∠ABC=∠AEF
∠BCA=∠EFA
∠BAC=∠EAF
∠1=∠2
图四中的对应边和角不明确,所以不能确定所有相等的边和角。
我们添加一组条件看看
新知典例
A
B
D
C
1
4
2
3
例2 图中△ABC与△ADC全等,AB=AD,请写出其余相等的边和角
解:DC=BC,AC=AC(公共边),∠1=∠2,∠3=∠4,∠D=∠B
变式 图中△ABC与△ADC全等,AB=DC,请写出其余相等的边和角
解:DC=AB,AC=CA(公共边),∠1=∠4,∠3=∠2,∠D=∠B
注意:解题时,要根据题意,找准对应边,不能以“想当然”为依据。
新知典例
∠ADE
∠E
∠A
ED
AD
AE
A
B
C
E
D
角
角
角
边
边
边
AB=
AC=
BC=
∠A=
∠B=
∠ACB=
例3 如图,已知△ABC≌△AED,请指出图中的对应边和对应角.
还有没有相等的线段?
BD=CE
小结:相等的角或边有互相重叠部分时,不重叠的部分也相等。
课堂总结
全等三角形
定义
表示
方法
有关
概念
性质
能够完全重合的两个三角形
对应顶点、对应边、对应角
对应边相等、对应角相等
用全等符号“ ”表示
≌
课堂练习
1.如图,△OAB≌△OCD,若∠A=80°,OB=3,则下列说法正确的是( )
A.∠COD=80° B.CD=3
C.∠D=20° D.OD=3
D
2.如图,△ACE≌△DBF,若AD=11cm,BC=5cm,则AB长为( )
A.6cm B.7cm
C.4cm D.3cm
D
课堂练习
3.如图,△ACE≌△DBF,若∠A=66°,∠E=78°,则∠FBD的度数为 .
36°
解:∵△ACE≌△DBF,∠A=66°,∠E=78°,
∴∠D=∠A=66°,∠F=∠E=78°,
∴∠FBD=180°﹣∠D﹣∠F=36°,
课堂练习
4.如图,△ABC≌△DBE,AB=6,AC=9,BE=5,则△ABC的周长为 .
20
解:∵△ABC≌△DBE,BE=5,
∴BC=BE=5,
∵AB=6,AC=9,
∴△ABC的周长=AB+AC+BC=6+9+5=20.
课堂练习
5.如图,已知△ABC≌△A′BC′,且A、A′、C三点在一条直线上,∠ABC=107°、∠CA′C′=81°,则∠A′BC= .
26°
解:∵△ABC≌△A′BC′ ∠ABC=107°
∴∠C=∠C′ ∠ABC=∠A′BC′=107°
∵∠A′DC=∠BDC
∴∠DA′C+∠A′CD=∠BDC′+∠DC′B
∴∠CA′C′=∠CBC′
∵∠CA′C′=81°
∴∠CBC′=81°
∴∠A′BC=∠ABC﹣∠CBC′=26°
D
课堂练习
6.∠B=∠D=90°,△ABC≌△CDE,B、C、D三点共线.试说明:∠ACE=90°.
证明:∵Rt△ABC≌Rt△CDE,
∴∠BCA=∠CED,
∵△DCE是直角三角形,
∴∠CED+∠ECD=90°,
∴∠BCA+∠ECD=90°,
∴∠ACE=180°﹣90°=90°
谢谢
人教版八年级上册
12.1全等三角形
知识回顾
1.三角形表示方法
顶点是A,B,C的三角形记作△ABC,
读作“三角形ABC”.
A
B
C
2.图中有几个三角形?用符号表示出这些三角形?
A
B
C
D
E
5个,它们分别是△ABE,△ABC, △BEC,△BCD,△ECD.
教学目标
1. 熟记全等形及全等三角形的概念;能够正确找出全等三角形的对应边、对应角.
2. 熟练掌握全等三角形的性质,并能灵活运用全等三角形的性质解决相应的几何问题.
3. 初步帮助学生建立平移、翻折、旋转三种图形变化与全等形的关系.
新知导入
这是我们的天安门城楼,它建于明朝永乐十五年(1416年),设计者为明代御用建筑匠师蒯(kuǎi)祥,历经数百年依旧雄伟、神圣。
问题1:我们放大看看,在图中我们能不能找出形状、大小相同建筑结构或图案呢?
新知导入
问题2 我们可以看到天安门上有大量形状、大小相同的建筑结构和图案,在自然界也存在大量这种情况,你能找出下列图片中形状、大小相同的部分吗?
同层的花瓣
猫的耳朵、眼睛
新知导入
问题3 为验证这些图案的形状、大小都相同,请将下列图形变化方法与图片进行连线,使这些部分能够重合。
平移
翻折
旋转
新知探究
知识点 1
全等图形的定义及性质
可以看到通过平移、翻折、旋转,可以使这些形状、大小都相同的图形完全重合,在我们身边大量存在的这些全等图形,就是今天我们要探究的主角。
全等图形的定义
能够完全重合的两个图形叫做全等图形.
全等图形的性质
如果两个图形全等,它们的形状和大小一定都相等.
综上所述,在我们身边有大量全等图形,我们先从最基本的三角形开始学习
新知探究
全等三角形的有关概念和表示方法
知识点 2
E
D
F
A
B
C
与全等图形一样,△ABC 叠到△DEF上,能够完全重合的两个三角形,叫作全等三角形.
把两个全等的三角形重叠到一起时,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角.
例如:点A与点D为一组对应顶点,AB与DE为一组对应边,∠C与∠F为一组对应角
新知探究
问题4 你能指出下图中两个全等三角形的对应顶点、对应边、对应角吗?
A
B
C
D
A
B
C
D
A
B
C
D
对应顶点:
对应边:
对应角:
A与A,B与D,C与C
AB与AD,
BC与DC,
AC与AC
∠ABC与∠ADC,
∠BCA与∠DCA,
∠BAC与∠DAC
A与C,B与D,C与A
AB与CD,
BC与AD,
AC与CA
∠ABC与∠CDA,
∠BCA与∠DAC,
∠BAC与∠DCA
A与D,B与C,C与B
AB与DC,
BC与CB,
AC与DB
∠ABC与∠DCB,
∠BCA与∠CBD,
∠A与∠D
新知探究
同时我们注意到,一个三角形通过平移、翻折、旋转后,所得到的三角形,能够与原来的三角形完全重合,所以我们将平移、翻折、旋转叫做全等变化。
即,一个图形经过平移、翻折、旋转后, 变化了,但 和 都没有改变,即平移、翻折、旋转前后的两个图形 .
形状
大小
全等
位置
A
B
C
G
E
F
A
C
B
D
A
B
C
D
新知探究
△ABC与△FDE全等,记作
△ABC≌△FDE
A
B
C
E
D
F
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
例如:
读作,△ABC全等于△FDE全等
注意:用“≌”记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
新知探究
全等三角形的性质
知识点 3
A
B
C
D
E
F
问题5 如图,△ABC≌△DEF,也就是两个三角形能够完全重合,你能找出相等的边和角吗?
相等的线段:AB=DE,AC=DF,BC=EF
相等的角:∠A=∠D,∠B=∠E,∠C=∠F
问题6 你有什么发现?
全等三角形的对应边相等,对应角相等。
新知小结
全等三角形的对应边相等,对应角相等
全等三角形的性质
∵△ABC≌△FDE,
∴A B=F D,A C=F E,B C=D E,(全等三角形对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E.(全等三角形对应角相等)
A
B
C
E
D
F
全等三角形的性质的几何语言
新知典例
A
D
F
C
E
B
1
2
A
B
D
C
1
4
2
3
E
A
B
C
F
1
2
例1 下图中红色与蓝色三角形全等,找出相等的线段和角?
A
B
C
D
F
相等的边
相等的角
AB=DE
BC=EF
AC=DF
BE=CF
∠B=∠1
∠2=∠F
∠A=∠D
AB=AF
BC=DF
AC=AD
BD=CF
∠B=∠F
∠BCA=∠ADC
∠BAC=∠DAF
∠BAD=∠FAC
AB=AE
BC=EF
AC=AF
∠ABC=∠AEF
∠BCA=∠EFA
∠BAC=∠EAF
∠1=∠2
图四中的对应边和角不明确,所以不能确定所有相等的边和角。
我们添加一组条件看看
新知典例
A
B
D
C
1
4
2
3
例2 图中△ABC与△ADC全等,AB=AD,请写出其余相等的边和角
解:DC=BC,AC=AC(公共边),∠1=∠2,∠3=∠4,∠D=∠B
变式 图中△ABC与△ADC全等,AB=DC,请写出其余相等的边和角
解:DC=AB,AC=CA(公共边),∠1=∠4,∠3=∠2,∠D=∠B
注意:解题时,要根据题意,找准对应边,不能以“想当然”为依据。
新知典例
∠ADE
∠E
∠A
ED
AD
AE
A
B
C
E
D
角
角
角
边
边
边
AB=
AC=
BC=
∠A=
∠B=
∠ACB=
例3 如图,已知△ABC≌△AED,请指出图中的对应边和对应角.
还有没有相等的线段?
BD=CE
小结:相等的角或边有互相重叠部分时,不重叠的部分也相等。
课堂总结
全等三角形
定义
表示
方法
有关
概念
性质
能够完全重合的两个三角形
对应顶点、对应边、对应角
对应边相等、对应角相等
用全等符号“ ”表示
≌
课堂练习
1.如图,△OAB≌△OCD,若∠A=80°,OB=3,则下列说法正确的是( )
A.∠COD=80° B.CD=3
C.∠D=20° D.OD=3
D
2.如图,△ACE≌△DBF,若AD=11cm,BC=5cm,则AB长为( )
A.6cm B.7cm
C.4cm D.3cm
D
课堂练习
3.如图,△ACE≌△DBF,若∠A=66°,∠E=78°,则∠FBD的度数为 .
36°
解:∵△ACE≌△DBF,∠A=66°,∠E=78°,
∴∠D=∠A=66°,∠F=∠E=78°,
∴∠FBD=180°﹣∠D﹣∠F=36°,
课堂练习
4.如图,△ABC≌△DBE,AB=6,AC=9,BE=5,则△ABC的周长为 .
20
解:∵△ABC≌△DBE,BE=5,
∴BC=BE=5,
∵AB=6,AC=9,
∴△ABC的周长=AB+AC+BC=6+9+5=20.
课堂练习
5.如图,已知△ABC≌△A′BC′,且A、A′、C三点在一条直线上,∠ABC=107°、∠CA′C′=81°,则∠A′BC= .
26°
解:∵△ABC≌△A′BC′ ∠ABC=107°
∴∠C=∠C′ ∠ABC=∠A′BC′=107°
∵∠A′DC=∠BDC
∴∠DA′C+∠A′CD=∠BDC′+∠DC′B
∴∠CA′C′=∠CBC′
∵∠CA′C′=81°
∴∠CBC′=81°
∴∠A′BC=∠ABC﹣∠CBC′=26°
D
课堂练习
6.∠B=∠D=90°,△ABC≌△CDE,B、C、D三点共线.试说明:∠ACE=90°.
证明:∵Rt△ABC≌Rt△CDE,
∴∠BCA=∠CED,
∵△DCE是直角三角形,
∴∠CED+∠ECD=90°,
∴∠BCA+∠ECD=90°,
∴∠ACE=180°﹣90°=90°
谢谢
