2022—2023学年人教版数学八年级上册13.3.1 等腰三角形的判定( 第2课时) 课件(共15张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册13.3.1 等腰三角形的判定( 第2课时) 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 175.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 07:25:46 | ||
图片预览




文档简介
(共15张PPT)
13.3 等腰三角形
第十三章 轴对称
第2课时 等腰三角形的判定
填空
1、等腰三角形一个底角为70°,它的另外两个角为__________________.
2、等腰三角形一个角为70°,它的另外两个角为__________________.
3、等腰三角形一个角为110°,它的另外两个角为___________.
70 °,40 °
70°,40° 或 55°,55°
35 °,35 °
回顾旧知,引入新知
在解决以上问题时,同学们都用了等腰三角形的什么性质?
反过来,如果一个三角形有两个角相等,那么它们所对的边相等吗?
思考
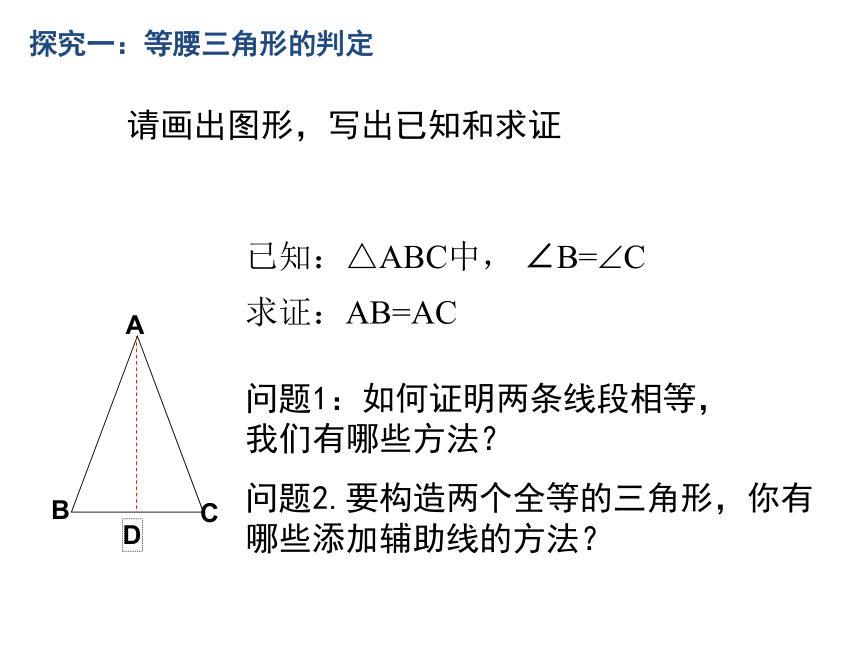
请画出图形,写出已知和求证
已知:△ABC中, ∠B= C
求证:AB=AC
问题1:如何证明两条线段相等,我们有哪些方法?
问题2.要构造两个全等的三角形,你有哪些添加辅助线的方法?
A
B
C
D
探究一:等腰三角形的判定
C
B
A
等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)
几何语言:
∵在△ABC中,∠B=∠C
∴AB=AC(等角对等边)
思考:等腰三角形的判定与性质进行比较,两者有什么区别?
A
B
C
D
2
1
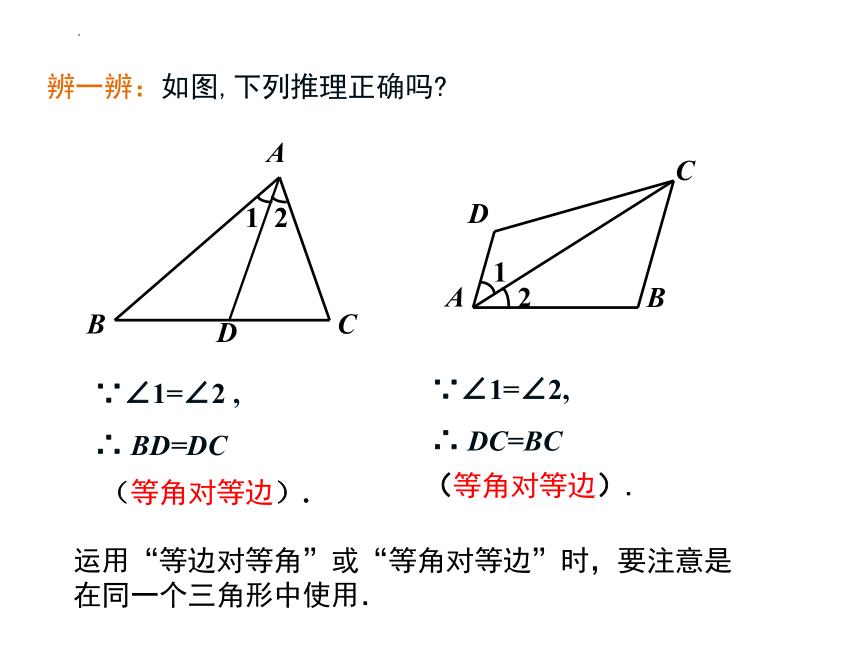
∵∠1=∠2 , ∴ BD=DC
(等角对等边).
∵∠1=∠2, ∴ DC=BC
A
B
C
D
2
1
(等角对等边).
辨一辨:如图,下列推理正确吗
运用“等边对等角”或“等角对等边”时,要注意是在同一个三角形中使用.
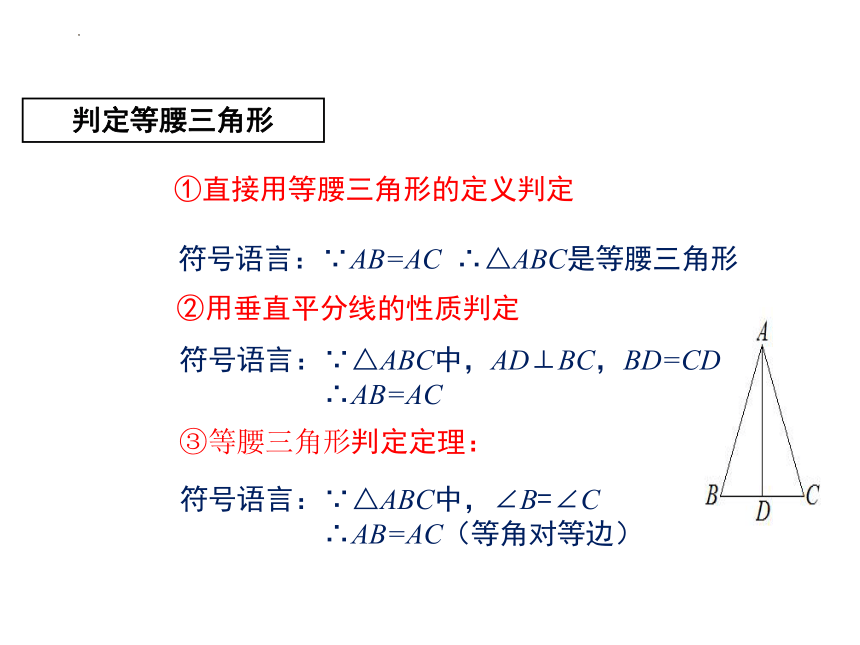
①直接用等腰三角形的定义判定
符号语言:∵AB=AC ∴△ABC是等腰三角形
②用垂直平分线的性质判定
符号语言:∵△ABC中,AD⊥BC,BD=CD
∴AB=AC
③等腰三角形判定定理:
符号语言:∵△ABC中,∠B=∠C
∴AB=AC(等角对等边)
判定等腰三角形
课堂练习
A
B
C
D
练习1 (书79页练习题1)如图,∠A =36°,∠DBC =36°,∠C =72°,分别计算∠ABD 和∠BDC的度数,并说明图中有哪些等腰三角形?
(书79页练习2)
2.如图,把一张长方形的纸沿着对角线折叠,
重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知: 如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
A
B
C
E
(
(
1
2
D
探究二:等腰三角形判定的应用(文字命题证明)
归纳:证明文字命题的一般步骤:
①分清命题的条件和结论;
②根据题意画出正确图形;
③结合图形写出“已知”、“求证”;
④分析题意,探索证题思路;
⑤依据思路写出证明过程.
书79页练习3:求证:如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
求证: △ABC是直角三角形
已知:△ABC,D为AC的中点,BD = AC.
课堂练习
探究三:等腰三角形判定的应用(条件作图)
例2:已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.
问题1:根据已知条件,我们应该先画出等腰三角形的哪条边,如何用尺规作出已知的长度?
问题3:如何作已知线段的垂直平分线?
注意:尺规作图要保留作图痕.
问题2:等腰三角形的高和底边有什么关系,在哪条直线上?
探究四:等腰三角形性质与判定的综合应用
例2.已知△ABC中,AB=AC,D、E分别是AB和BC上的点,连结DE并延长与AC的延长线交于点F,若DE=EF.
求证:DB=CF.
书79页练习4 如图,AC和BD相交于O点,且AB ∥ DC,OA = OB. 求证OC = OD.
归纳总结
1.通过今天的学习,你有了哪些证明两条线段相等的方法?
2.证明命题时的一般步骤有哪些?
3.你还有哪些疑惑?
13.3 等腰三角形
第十三章 轴对称
第2课时 等腰三角形的判定
填空
1、等腰三角形一个底角为70°,它的另外两个角为__________________.
2、等腰三角形一个角为70°,它的另外两个角为__________________.
3、等腰三角形一个角为110°,它的另外两个角为___________.
70 °,40 °
70°,40° 或 55°,55°
35 °,35 °
回顾旧知,引入新知
在解决以上问题时,同学们都用了等腰三角形的什么性质?
反过来,如果一个三角形有两个角相等,那么它们所对的边相等吗?
思考
请画出图形,写出已知和求证
已知:△ABC中, ∠B= C
求证:AB=AC
问题1:如何证明两条线段相等,我们有哪些方法?
问题2.要构造两个全等的三角形,你有哪些添加辅助线的方法?
A
B
C
D
探究一:等腰三角形的判定
C
B
A
等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)
几何语言:
∵在△ABC中,∠B=∠C
∴AB=AC(等角对等边)
思考:等腰三角形的判定与性质进行比较,两者有什么区别?
A
B
C
D
2
1
∵∠1=∠2 , ∴ BD=DC
(等角对等边).
∵∠1=∠2, ∴ DC=BC
A
B
C
D
2
1
(等角对等边).
辨一辨:如图,下列推理正确吗
运用“等边对等角”或“等角对等边”时,要注意是在同一个三角形中使用.
①直接用等腰三角形的定义判定
符号语言:∵AB=AC ∴△ABC是等腰三角形
②用垂直平分线的性质判定
符号语言:∵△ABC中,AD⊥BC,BD=CD
∴AB=AC
③等腰三角形判定定理:
符号语言:∵△ABC中,∠B=∠C
∴AB=AC(等角对等边)
判定等腰三角形
课堂练习
A
B
C
D
练习1 (书79页练习题1)如图,∠A =36°,∠DBC =36°,∠C =72°,分别计算∠ABD 和∠BDC的度数,并说明图中有哪些等腰三角形?
(书79页练习2)
2.如图,把一张长方形的纸沿着对角线折叠,
重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知: 如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.
A
B
C
E
(
(
1
2
D
探究二:等腰三角形判定的应用(文字命题证明)
归纳:证明文字命题的一般步骤:
①分清命题的条件和结论;
②根据题意画出正确图形;
③结合图形写出“已知”、“求证”;
④分析题意,探索证题思路;
⑤依据思路写出证明过程.
书79页练习3:求证:如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
求证: △ABC是直角三角形
已知:△ABC,D为AC的中点,BD = AC.
课堂练习
探究三:等腰三角形判定的应用(条件作图)
例2:已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.
问题1:根据已知条件,我们应该先画出等腰三角形的哪条边,如何用尺规作出已知的长度?
问题3:如何作已知线段的垂直平分线?
注意:尺规作图要保留作图痕.
问题2:等腰三角形的高和底边有什么关系,在哪条直线上?
探究四:等腰三角形性质与判定的综合应用
例2.已知△ABC中,AB=AC,D、E分别是AB和BC上的点,连结DE并延长与AC的延长线交于点F,若DE=EF.
求证:DB=CF.
书79页练习4 如图,AC和BD相交于O点,且AB ∥ DC,OA = OB. 求证OC = OD.
归纳总结
1.通过今天的学习,你有了哪些证明两条线段相等的方法?
2.证明命题时的一般步骤有哪些?
3.你还有哪些疑惑?
