2022-2023学年人教版九年级数学上册 21.3 实际问题与一元二次方程(面积问题)课件(共14张PPT)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册 21.3 实际问题与一元二次方程(面积问题)课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 07:53:28 | ||
图片预览




文档简介
(共14张PPT)
第二十一章 一元二次方程
第10课时 实际问题与一元二次方程(三)(面积问题1)
知识点1 “边框”问题
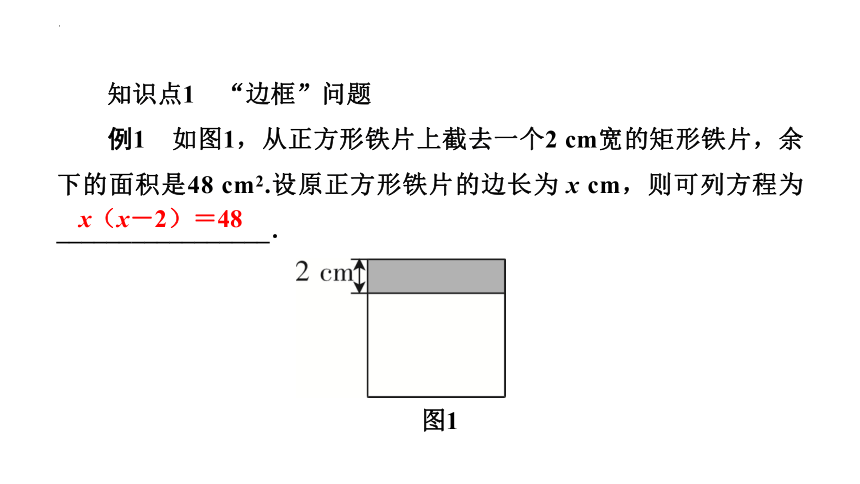
例1 如图1,从正方形铁片上截去一个2 cm宽的矩形铁片,余下的面积是48 cm2.设原正方形铁片的边长为 x cm,则可列方程为_________________.
图1
x(x-2)=48
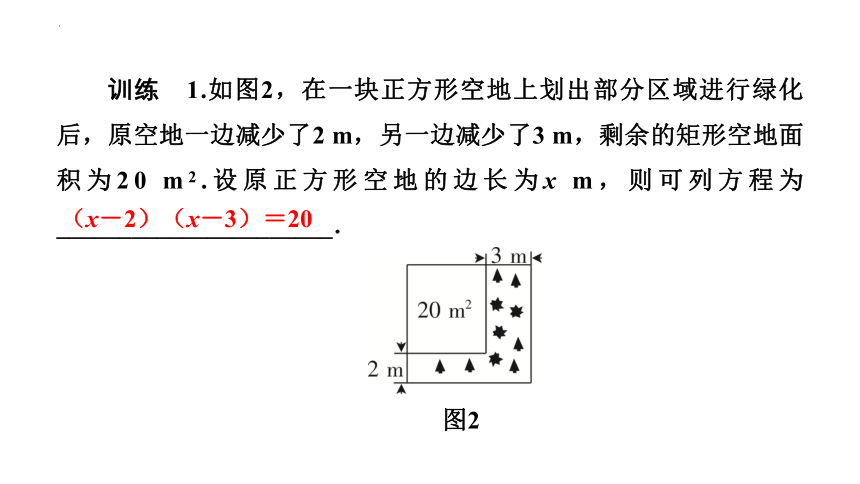
训练 1.如图2,在一块正方形空地上划出部分区域进行绿化后,原空地一边减少了2 m,另一边减少了3 m,剩余的矩形空地面积为20 m2.设原正方形空地的边长为x m,则可列方程为______________________.
图2
(x-2)(x-3)=20
例2 如图3,幼儿园某教室矩形地面的长为8 m,宽为5 m,现准备在地面正中间铺设一块面积为18 m2的地毯,四周未铺地毯的条形区域的宽度都相同,求四周未铺地毯的条形区域的宽度是多少?
解:设四周未铺地毯的条形区域的宽度是x m,
则地毯的长为__________m,宽为__________m.
由题意,得________________________.
整理,得_________________.
解得x1=________,x2=________.
又5-2x______0,∴x________.∴x=______.
答:四周未铺地毯的条形区域的宽度是________m.
图3
(8-2x)
(5-2x)
(8-2x)(5-2x)=18
2x2-13x+11=0
1
>
1
1
训练 2.如图4,将一张长为16 cm,宽为12 cm的照片装进面积为320 cm2的矩形相框,照片四周与相框四周之间的宽度相等,求这个宽度.
图4
解:设这个宽度为x cm,则相框的长为(16+2x)cm,宽为(12+2x)cm.
由题意,得(16+2x)(12+2x)=320.解得x1=2,x2=-16(舍去).
答:这个宽度为2 cm.
知识点2 “小路”问题
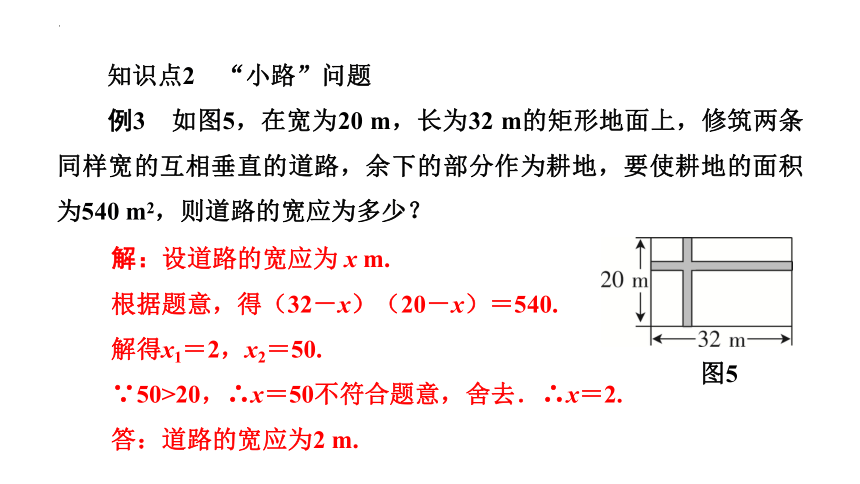
例3 如图5,在宽为20 m,长为32 m的矩形地面上,修筑两条同样宽的互相垂直的道路,余下的部分作为耕地,要使耕地的面积为540 m2,则道路的宽应为多少?
图5
解:设道路的宽应为 x m.
根据题意,得(32-x)(20-x)=540.
解得x1=2,x2=50.
∵50>20,∴x=50不符合题意,舍去.∴x=2.
答:道路的宽应为2 m.
训练 3.改善小区环境,争创文明家园.如图6,某社区决定在一块长(AD)16 m,宽(AB)9 m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分为草坪.要使草坪部分的总面积为112 m2,则小路的宽应为多少?
图6
解:设小路的宽应为 x m.
根据题意,得(16-2x)(9-x)=112.
解得x1=1,x2=16.
∵16>9,∴x=16不符合题意,舍去.∴x=1.
答:小路的宽应为1 m.
1.如图7,在一块长15 m,宽10 m的矩形空地上,修建两条同样宽的互相垂直的道路,剩余部分用来绿化,要使绿化面积为126 m2,则修建的路宽应为________m.
基础过关
图7
1
2.某中学有一块长40 m,宽30 m的矩形空地,该中学计划在这块空地上划出四分之一的区域种花,小禹同学的设计方案如图8所示.设花带的宽度为x m,则可列方程为______________________________.
(40-2x)(30-x)=900
图8
3.2020年初,受新型冠状病毒的影响,口罩成为最紧缺的物资之一,某服装厂快速转型生产某种型号的矩形防护口罩.如图9,已知该口罩的长为18 cm,宽为9 cm,口罩的上压边宽度是下压边宽度的2倍,左右压边与下压边同宽(图中阴影部分).
(1)设口罩的下压边宽度为x cm,则口罩的上压边宽度为__________cm.
图9
2x
(2)要使口罩内部的有效面积达到96 cm2,则口罩的下压边宽度应为多少?
图9
解:依题意,得(18-2x)(9-3x)=96.
解得x1=1,x2=11(舍去).
答:口罩的下压边宽度应为1 cm.
4.中国古代数学家杨辉的《田亩比类乘除捷法》中记载:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?”翻译成数学问题是:一块矩形田地的面积为864平方步,它的宽比长少12步,问它的长与宽各多少步?利用方程思想,设宽为 x 步,则依题意列方程为_____________________.
能力提升
x(x+12)=864
5.某校为迎接2022冬奥会,举办了“冰雪运动进校园”活动,计划在校园内一块长50 m,宽20 m的矩形空地上铺设两块完全相同的矩形冰场,如图10,要使两块矩形冰场之间及周边留有宽度相等的通道,且两块矩形冰场的面积是原空地面积的 ,求通道的宽度.
图10
6.【应用意识】如图11,在宽为25米,长为35米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪.要使草坪的面积为540平方米,设道路的宽为x米,则可列方程为( )
A.35×25-35x-25x=540
B.(35-x)(25-x)=540
C.35x+25x=540
D.(35-x)(25-x)+x2=540
核心素养
图11
B
第二十一章 一元二次方程
第10课时 实际问题与一元二次方程(三)(面积问题1)
知识点1 “边框”问题
例1 如图1,从正方形铁片上截去一个2 cm宽的矩形铁片,余下的面积是48 cm2.设原正方形铁片的边长为 x cm,则可列方程为_________________.
图1
x(x-2)=48
训练 1.如图2,在一块正方形空地上划出部分区域进行绿化后,原空地一边减少了2 m,另一边减少了3 m,剩余的矩形空地面积为20 m2.设原正方形空地的边长为x m,则可列方程为______________________.
图2
(x-2)(x-3)=20
例2 如图3,幼儿园某教室矩形地面的长为8 m,宽为5 m,现准备在地面正中间铺设一块面积为18 m2的地毯,四周未铺地毯的条形区域的宽度都相同,求四周未铺地毯的条形区域的宽度是多少?
解:设四周未铺地毯的条形区域的宽度是x m,
则地毯的长为__________m,宽为__________m.
由题意,得________________________.
整理,得_________________.
解得x1=________,x2=________.
又5-2x______0,∴x________.∴x=______.
答:四周未铺地毯的条形区域的宽度是________m.
图3
(8-2x)
(5-2x)
(8-2x)(5-2x)=18
2x2-13x+11=0
1
>
1
1
训练 2.如图4,将一张长为16 cm,宽为12 cm的照片装进面积为320 cm2的矩形相框,照片四周与相框四周之间的宽度相等,求这个宽度.
图4
解:设这个宽度为x cm,则相框的长为(16+2x)cm,宽为(12+2x)cm.
由题意,得(16+2x)(12+2x)=320.解得x1=2,x2=-16(舍去).
答:这个宽度为2 cm.
知识点2 “小路”问题
例3 如图5,在宽为20 m,长为32 m的矩形地面上,修筑两条同样宽的互相垂直的道路,余下的部分作为耕地,要使耕地的面积为540 m2,则道路的宽应为多少?
图5
解:设道路的宽应为 x m.
根据题意,得(32-x)(20-x)=540.
解得x1=2,x2=50.
∵50>20,∴x=50不符合题意,舍去.∴x=2.
答:道路的宽应为2 m.
训练 3.改善小区环境,争创文明家园.如图6,某社区决定在一块长(AD)16 m,宽(AB)9 m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分为草坪.要使草坪部分的总面积为112 m2,则小路的宽应为多少?
图6
解:设小路的宽应为 x m.
根据题意,得(16-2x)(9-x)=112.
解得x1=1,x2=16.
∵16>9,∴x=16不符合题意,舍去.∴x=1.
答:小路的宽应为1 m.
1.如图7,在一块长15 m,宽10 m的矩形空地上,修建两条同样宽的互相垂直的道路,剩余部分用来绿化,要使绿化面积为126 m2,则修建的路宽应为________m.
基础过关
图7
1
2.某中学有一块长40 m,宽30 m的矩形空地,该中学计划在这块空地上划出四分之一的区域种花,小禹同学的设计方案如图8所示.设花带的宽度为x m,则可列方程为______________________________.
(40-2x)(30-x)=900
图8
3.2020年初,受新型冠状病毒的影响,口罩成为最紧缺的物资之一,某服装厂快速转型生产某种型号的矩形防护口罩.如图9,已知该口罩的长为18 cm,宽为9 cm,口罩的上压边宽度是下压边宽度的2倍,左右压边与下压边同宽(图中阴影部分).
(1)设口罩的下压边宽度为x cm,则口罩的上压边宽度为__________cm.
图9
2x
(2)要使口罩内部的有效面积达到96 cm2,则口罩的下压边宽度应为多少?
图9
解:依题意,得(18-2x)(9-3x)=96.
解得x1=1,x2=11(舍去).
答:口罩的下压边宽度应为1 cm.
4.中国古代数学家杨辉的《田亩比类乘除捷法》中记载:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?”翻译成数学问题是:一块矩形田地的面积为864平方步,它的宽比长少12步,问它的长与宽各多少步?利用方程思想,设宽为 x 步,则依题意列方程为_____________________.
能力提升
x(x+12)=864
5.某校为迎接2022冬奥会,举办了“冰雪运动进校园”活动,计划在校园内一块长50 m,宽20 m的矩形空地上铺设两块完全相同的矩形冰场,如图10,要使两块矩形冰场之间及周边留有宽度相等的通道,且两块矩形冰场的面积是原空地面积的 ,求通道的宽度.
图10
6.【应用意识】如图11,在宽为25米,长为35米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪.要使草坪的面积为540平方米,设道路的宽为x米,则可列方程为( )
A.35×25-35x-25x=540
B.(35-x)(25-x)=540
C.35x+25x=540
D.(35-x)(25-x)+x2=540
核心素养
图11
B
同课章节目录
