2022-2023学年北师大版八年级数学上册第一章 勾股定理 复习与小结 课件(共20张PPT)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学上册第一章 勾股定理 复习与小结 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 368.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 22:45:38 | ||
图片预览




文档简介
(共20张PPT)
北师大版数学 八年级上册
第一章 勾股定理
教学课件
《勾股定理》复习与小结
知识体系
第一章 勾股定理
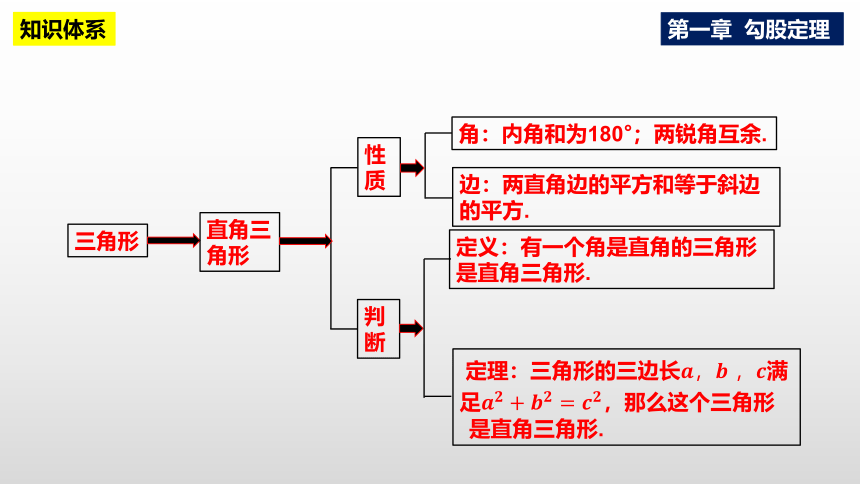
三角形
直角三角形
性质
判断
角:内角和为180°;两锐角互余.
边:两直角边的平方和等于斜边的平方.
定义:有一个角是直角的三角形是直角三角形.
定理:三角形的三边长 满足,那么这个三角形
是直角三角形.
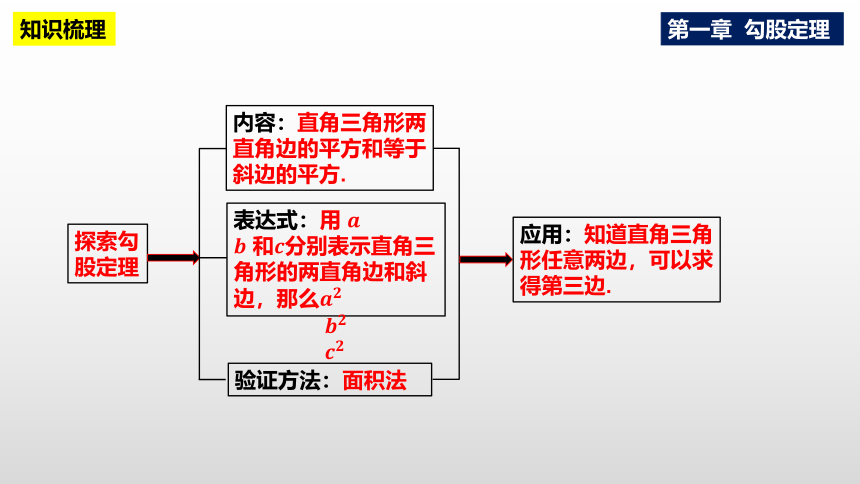
探索勾股定理
内容:直角三角形两直角边的平方和等于斜边的平方.
表达式:用 和分别表示直角三角形的两直角边和斜边,那么
验证方法:面积法
应用:知道直角三角形任意两边,可以求得第三边.
知识梳理
第一章 勾股定理
知识梳理
第一章 勾股定理
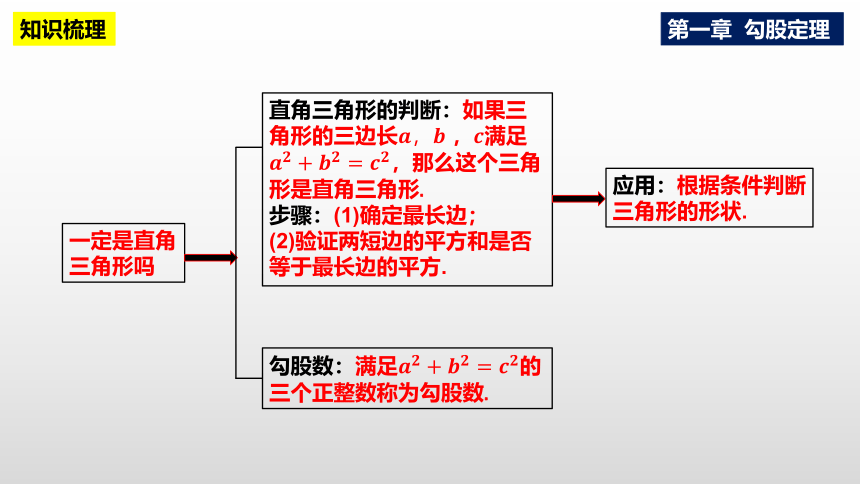
一定是直角三角形吗
直角三角形的判断:如果三角形的三边长 ,满足,那么这个三角形是直角三角形.
步骤:(1)确定最长边;
(2)验证两短边的平方和是否等于最长边的平方.
勾股数:满足的三个正整数称为勾股数.
应用:根据条件判断三角形的形状.
知识梳理
第一章 勾股定理
勾股定理的应用
知道直角三角形任意两边求第三边.
解决生活中实际问题
最短路程问题及折叠图形中的面积问题.
构造直角三角形模型
基础训练
第一章 勾股定理
1. 下列说法正确的是( )
A. 若是的△ABC的三边,则
B. 若是的Rt△ABC的三边,则
C. 若是的Rt△ABC的三边,则
D. 若是的△ABC的三边,且,则∠A=90°
D
2. 如图是商场的台阶的示意图,已知每级台阶的宽度都是20cm,每级台阶的高度都是15cm,则连接AB的线段长为( )
A. 100cm
B. 150cm
C. 200cm
D. 250cm
A
B
基础训练
第一章 勾股定理
B
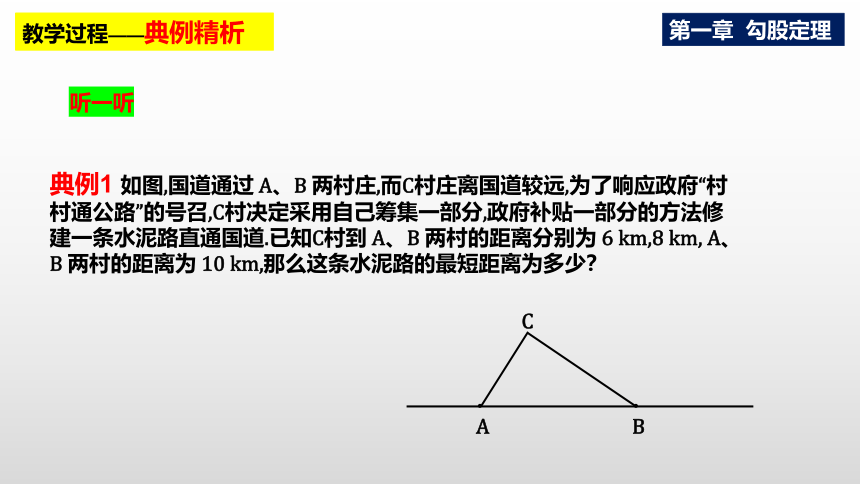
典例1 如图,国道通过 A、B 两村庄,而C村庄离国道较远,为了响应政府“村村通公路”的号召,C村决定采用自己筹集一部分,政府补贴一部分的方法修建一条水泥路直通国道.已知C村到 A、B 两村的距离分别为 6 km,8 km, A、B 两村的距离为 10 km,那么这条水泥路的最短距离为多少?
A
B
C
教学过程——典例精析
第一章 勾股定理
听一听
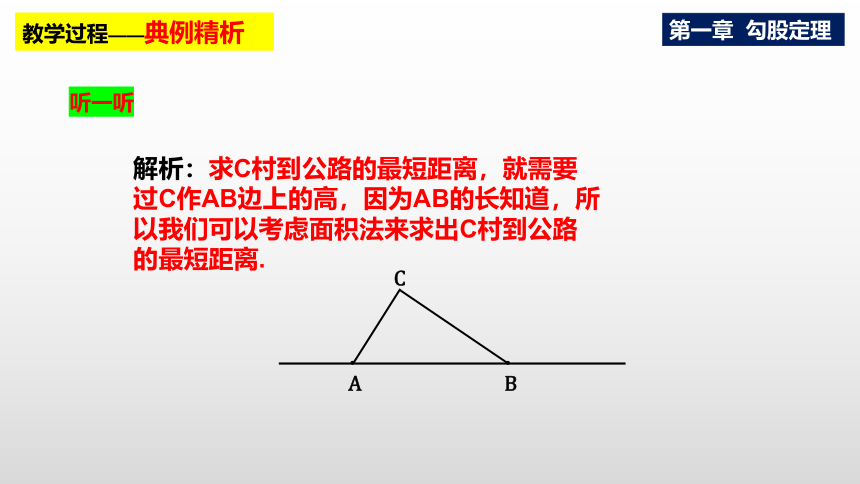
解析:求C村到公路的最短距离,就需要过C作AB边上的高,因为AB的长知道,所以我们可以考虑面积法来求出C村到公路的最短距离.
A
B
C
教学过程——典例精析
第一章 勾股定理
听一听
A
B
C
解:过C作CD⊥AB于D.
在△ABC中,AB=10,AC=6,BC=8
∴AC2+BC2=62+82=102=AB2
∴△ABC是直角三角形,∠C=90°.
D
∵S△ABC=.
∴.
∴.
故这条水泥路的最短距离为4.8km.
教学过程——典例精析
第一章 勾股定理
听一听
典例2 如图直线代表河岸,在河岸有两个村庄A和B,A村距河岸2km,B村距河岸4km,A、B两村的水平距离是8km. 两村要共同出资修建一个供水站向两村供水,为了节省资金,要求两村到供水站的距离和最小,这样用的水管就最短.
(1)在上画出供水站的位置P.
(2)若建供水站要花50000元,每千米水管及其他费用要花5000元,求供水站建成后共计要花多少钱?
A
B
教学过程——典例精析
第一章 勾股定理
听一听
A
B
解析:这是一个关于动点问题中的最小值问题.由于A、B两点是定点,P点时动点,所以我们可以利用轴对称,使点A和点B在同一直线上,当这条直线与相交时,交点即为P点的位置.
教学过程——典例精析
第一章 勾股定理
听一听
A
B
解:(1)供水站P的位置如图所示.
P
A’
(2)过B作BM⊥,过A’作A’M⊥BM于M.
M
由已知可得A’M=8,BM=2+4=6.
在Rt△AMB中,A’B2=AM2+BM2=82+62=100
解得A’B=10
5000×10+50000=100000.
故供水站修建完成后共计要花100000元.
教学过程——典例精析
第一章 勾股定理
听一听
典例3 如图,长方形 ABCD 中,AB=3,AD=9,将此长方形折叠,使点 D与点B 重合,折痕为 EF,求△ABE 的面积。
教学过程——典例精析
第一章 勾股定理
听一听
解析:折叠问题中,要找到折叠前后相等的线段或角,注意这些线段与其他线段的关系,再利用勾股定理建立方程. 所以解答这类问题要注意应用方程思想.
教学过程——典例精析
第一章 勾股定理
听一听
解:设AE=,则DE=BE=9 ,
在Rt△ABE中,BE2=AB2+AE2
即(9-)2=32+2
解得=4
∴S△ABE==6
思考:你能求出折痕EF的长吗?
教学过程——典例精析
第一章 勾股定理
听一听
教学过程——随堂练习
第一章 勾股定理
练一练
已知三角形的一条边为15,另一条边为41,第三边上的高为9,求这个三角形的面积.
教学过程——课堂小结
第一章 勾股定理
记一记
利用勾股定理及其逆定理解决实际问题的思路——构造直角三角形模型——利用勾股定理——建立方程——解决问题.
课后巩固——分层作业
第一章 勾股定理
练一练
第一层:课本第16页复习题第3、4、5题
第二层:课本第16页复习题第12、13、14题.
结束新课
感谢聆听
第一章 勾股定理
北师大版数学 八年级上册
第一章 勾股定理
教学课件
《勾股定理》复习与小结
知识体系
第一章 勾股定理
三角形
直角三角形
性质
判断
角:内角和为180°;两锐角互余.
边:两直角边的平方和等于斜边的平方.
定义:有一个角是直角的三角形是直角三角形.
定理:三角形的三边长 满足,那么这个三角形
是直角三角形.
探索勾股定理
内容:直角三角形两直角边的平方和等于斜边的平方.
表达式:用 和分别表示直角三角形的两直角边和斜边,那么
验证方法:面积法
应用:知道直角三角形任意两边,可以求得第三边.
知识梳理
第一章 勾股定理
知识梳理
第一章 勾股定理
一定是直角三角形吗
直角三角形的判断:如果三角形的三边长 ,满足,那么这个三角形是直角三角形.
步骤:(1)确定最长边;
(2)验证两短边的平方和是否等于最长边的平方.
勾股数:满足的三个正整数称为勾股数.
应用:根据条件判断三角形的形状.
知识梳理
第一章 勾股定理
勾股定理的应用
知道直角三角形任意两边求第三边.
解决生活中实际问题
最短路程问题及折叠图形中的面积问题.
构造直角三角形模型
基础训练
第一章 勾股定理
1. 下列说法正确的是( )
A. 若是的△ABC的三边,则
B. 若是的Rt△ABC的三边,则
C. 若是的Rt△ABC的三边,则
D. 若是的△ABC的三边,且,则∠A=90°
D
2. 如图是商场的台阶的示意图,已知每级台阶的宽度都是20cm,每级台阶的高度都是15cm,则连接AB的线段长为( )
A. 100cm
B. 150cm
C. 200cm
D. 250cm
A
B
基础训练
第一章 勾股定理
B
典例1 如图,国道通过 A、B 两村庄,而C村庄离国道较远,为了响应政府“村村通公路”的号召,C村决定采用自己筹集一部分,政府补贴一部分的方法修建一条水泥路直通国道.已知C村到 A、B 两村的距离分别为 6 km,8 km, A、B 两村的距离为 10 km,那么这条水泥路的最短距离为多少?
A
B
C
教学过程——典例精析
第一章 勾股定理
听一听
解析:求C村到公路的最短距离,就需要过C作AB边上的高,因为AB的长知道,所以我们可以考虑面积法来求出C村到公路的最短距离.
A
B
C
教学过程——典例精析
第一章 勾股定理
听一听
A
B
C
解:过C作CD⊥AB于D.
在△ABC中,AB=10,AC=6,BC=8
∴AC2+BC2=62+82=102=AB2
∴△ABC是直角三角形,∠C=90°.
D
∵S△ABC=.
∴.
∴.
故这条水泥路的最短距离为4.8km.
教学过程——典例精析
第一章 勾股定理
听一听
典例2 如图直线代表河岸,在河岸有两个村庄A和B,A村距河岸2km,B村距河岸4km,A、B两村的水平距离是8km. 两村要共同出资修建一个供水站向两村供水,为了节省资金,要求两村到供水站的距离和最小,这样用的水管就最短.
(1)在上画出供水站的位置P.
(2)若建供水站要花50000元,每千米水管及其他费用要花5000元,求供水站建成后共计要花多少钱?
A
B
教学过程——典例精析
第一章 勾股定理
听一听
A
B
解析:这是一个关于动点问题中的最小值问题.由于A、B两点是定点,P点时动点,所以我们可以利用轴对称,使点A和点B在同一直线上,当这条直线与相交时,交点即为P点的位置.
教学过程——典例精析
第一章 勾股定理
听一听
A
B
解:(1)供水站P的位置如图所示.
P
A’
(2)过B作BM⊥,过A’作A’M⊥BM于M.
M
由已知可得A’M=8,BM=2+4=6.
在Rt△AMB中,A’B2=AM2+BM2=82+62=100
解得A’B=10
5000×10+50000=100000.
故供水站修建完成后共计要花100000元.
教学过程——典例精析
第一章 勾股定理
听一听
典例3 如图,长方形 ABCD 中,AB=3,AD=9,将此长方形折叠,使点 D与点B 重合,折痕为 EF,求△ABE 的面积。
教学过程——典例精析
第一章 勾股定理
听一听
解析:折叠问题中,要找到折叠前后相等的线段或角,注意这些线段与其他线段的关系,再利用勾股定理建立方程. 所以解答这类问题要注意应用方程思想.
教学过程——典例精析
第一章 勾股定理
听一听
解:设AE=,则DE=BE=9 ,
在Rt△ABE中,BE2=AB2+AE2
即(9-)2=32+2
解得=4
∴S△ABE==6
思考:你能求出折痕EF的长吗?
教学过程——典例精析
第一章 勾股定理
听一听
教学过程——随堂练习
第一章 勾股定理
练一练
已知三角形的一条边为15,另一条边为41,第三边上的高为9,求这个三角形的面积.
教学过程——课堂小结
第一章 勾股定理
记一记
利用勾股定理及其逆定理解决实际问题的思路——构造直角三角形模型——利用勾股定理——建立方程——解决问题.
课后巩固——分层作业
第一章 勾股定理
练一练
第一层:课本第16页复习题第3、4、5题
第二层:课本第16页复习题第12、13、14题.
结束新课
感谢聆听
第一章 勾股定理
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
