数学人教A版(,2019)必修第一册4.4.2对数函数的图象和性质(共15张ppt)
文档属性
| 名称 | 数学人教A版(,2019)必修第一册4.4.2对数函数的图象和性质(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 757.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 14:15:24 | ||
图片预览






文档简介
(共15张PPT)
第四章 指数函数与对数函数
4.4.2 对数函数图象与性质
教学目标:
1、理解并掌握对数函数的图像和性质;
2、会用对数函数的图像和性质解决相关问题.
一 新课引入
1 对数函数的定义
2 换底公式的作用
3 指数函数与对数函数的关系?
二 讲授新课
与研究指数函数一样,我们首先画出其图像,然后借助其图像研究其性质。
先画y=log2 x 的图像。列表如右:
描点作图:
y
x y
0.5 -1
1 0
2 1
4 2
8 3
16 4
0.25 -2
y
y=1og2 x
O
x
1
画图如右:
也可以用同样的方法画出:
还可以用换底公式来解决:
=log2 x-1 =-log2 x,两者的图像关于轴对称
的图象
这就是说,如果确定两个函数的图象是关于x轴对称的,就可以利用y=log2 x精确地画出的图象了。
为了得到对数函数y=logax的性质,我们还需要画出更多的具体的对数函数的图像进行观察。
继续选取底为 a=3,a= ,a=4,a=的对数函数的图像进行观察。
在同一个坐标系内
画图如右:
2
1
-1
-2
1
2
4
O
y
x
3
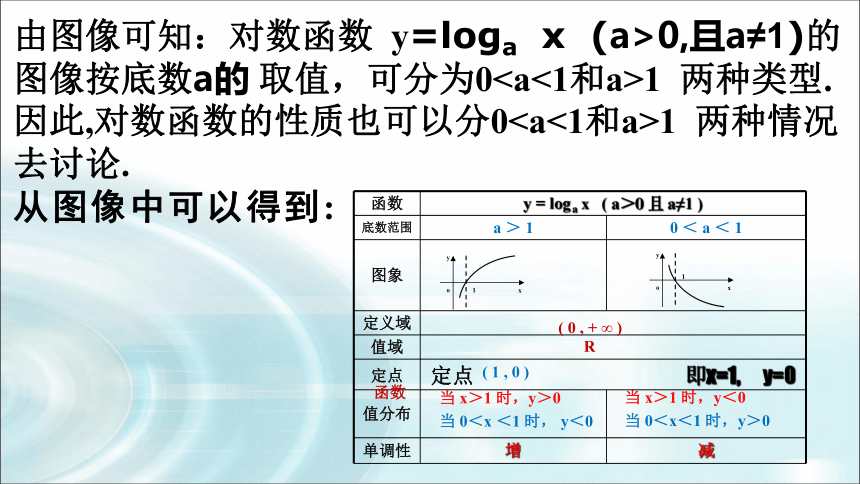
由图像可知:对数函数 y=loga x (a>0,且a≠1)的图像按底数a的 取值,可分为01 两种类型.因此,对数函数的性质也可以分01 两种情况去讨论.
从图像中可以得到:
函数 y = log a x ( a>0 且 a≠1 )
底数范围 a > 1 0 < a < 1
图象
定义域
值域
定点 定点 即x=1, y=0
值分布
单调性 增 减
1
x
y
o
1
x
y
o
( 0 , + ∞ )
R
( 1 , 0 )
当 x>1 时,y>0
当 0<x <1 时, y<0
当 x>1 时,y<0
当 0<x<1 时,y>0
函数
跟踪练习:
1 .函数 f (x)=logax的图象必经过定点( )
2 函数 f (x)=loga(x-2)-2的图象必经过定点( ) 3 函数y=logax ,若y >0 (a>0,且a≠1),分别求a、x取值范围;若y <0 (a>0,且a≠1),再回答同样的问题。
分析:
对应的对数值是0.
对于3,当a>1、x>1时,logax >0
当00
结合图形,解决若y <0 时的问题。
例2 .比较下列各组数中两个值的大小:
(1)
(2)
(3)
分析:(1)对于y=log2x,其在(0,+∞)上增函数
∵
∴
(2)对于y=log0.3x,其在(0,+∞)上减函数
∵
∴
(3)
分情况讨论:
当05.1<5.9
∴
当a>1,logax 在(0,+∞)上是增函数
5.1<5.9 ∴
三 课堂练习
.如图,若C1,C2分别为函数y=logax和y=logbx的图象,则( )
A.0C.a>b>1 D.b>a>1
分析:令y=1,y=loga x 的图象过点(a,1),y=logb x 的图象过点(b,1).如图
则0也可以取y=-1
同理可得:>>1
则0y=logax
1
y=logbx
a
b
-1
三 课堂小结
1 对数函数的图象与性质?
2 在应用数函数性质时应注意什么问题?
五 作业
课本P135 1,2
第四章 指数函数与对数函数
4.4.2 对数函数图象与性质
教学目标:
1、理解并掌握对数函数的图像和性质;
2、会用对数函数的图像和性质解决相关问题.
一 新课引入
1 对数函数的定义
2 换底公式的作用
3 指数函数与对数函数的关系?
二 讲授新课
与研究指数函数一样,我们首先画出其图像,然后借助其图像研究其性质。
先画y=log2 x 的图像。列表如右:
描点作图:
y
x y
0.5 -1
1 0
2 1
4 2
8 3
16 4
0.25 -2
y
y=1og2 x
O
x
1
画图如右:
也可以用同样的方法画出:
还可以用换底公式来解决:
=log2 x-1 =-log2 x,两者的图像关于轴对称
的图象
这就是说,如果确定两个函数的图象是关于x轴对称的,就可以利用y=log2 x精确地画出的图象了。
为了得到对数函数y=logax的性质,我们还需要画出更多的具体的对数函数的图像进行观察。
继续选取底为 a=3,a= ,a=4,a=的对数函数的图像进行观察。
在同一个坐标系内
画图如右:
2
1
-1
-2
1
2
4
O
y
x
3
由图像可知:对数函数 y=loga x (a>0,且a≠1)的图像按底数a的 取值,可分为0
从图像中可以得到:
函数 y = log a x ( a>0 且 a≠1 )
底数范围 a > 1 0 < a < 1
图象
定义域
值域
定点 定点 即x=1, y=0
值分布
单调性 增 减
1
x
y
o
1
x
y
o
( 0 , + ∞ )
R
( 1 , 0 )
当 x>1 时,y>0
当 0<x <1 时, y<0
当 x>1 时,y<0
当 0<x<1 时,y>0
函数
跟踪练习:
1 .函数 f (x)=logax的图象必经过定点( )
2 函数 f (x)=loga(x-2)-2的图象必经过定点( ) 3 函数y=logax ,若y >0 (a>0,且a≠1),分别求a、x取值范围;若y <0 (a>0,且a≠1),再回答同样的问题。
分析:
对应的对数值是0.
对于3,当a>1、x>1时,logax >0
当0
结合图形,解决若y <0 时的问题。
例2 .比较下列各组数中两个值的大小:
(1)
(2)
(3)
分析:(1)对于y=log2x,其在(0,+∞)上增函数
∵
∴
(2)对于y=log0.3x,其在(0,+∞)上减函数
∵
∴
(3)
分情况讨论:
当0
∴
当a>1,logax 在(0,+∞)上是增函数
5.1<5.9 ∴
三 课堂练习
.如图,若C1,C2分别为函数y=logax和y=logbx的图象,则( )
A.0
分析:令y=1,y=loga x 的图象过点(a,1),y=logb x 的图象过点(b,1).如图
则0
同理可得:>>1
则0
1
y=logbx
a
b
-1
三 课堂小结
1 对数函数的图象与性质?
2 在应用数函数性质时应注意什么问题?
五 作业
课本P135 1,2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
