数学人教A版(2019)必修第一册4.5.1函数的零点与方程的根(共22张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.5.1函数的零点与方程的根(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-14 09:38:35 | ||
图片预览








文档简介
(共22张PPT)
4.5.1
函数的零点
与方程的解
中外历史上的方程求解
在人类用智慧架设的无数座从未知通向已知的金桥中,方程的求解是其中璀璨的一座。虽然今天我们可以从教科书中了解各式各样方程的解法,但这一切却经历了相当漫长的岁月.
约公元50~100年编成的《九章算术》给出了一次方程、二次方程和正系数三次方程的求解方法.
情境引入
中外历史上的方程求解
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法。
11世纪,北宋数学家贾宪给出了三次及三次以上的方程的解法.
情境引入
中外历史上的方程求解
国外数学家对方程求解亦有很多研究。9世纪以后,先后发现了一次、二次、三次、四次方程的求解方法。
由于实际问题的需要,我们经常需要寻求函数y=f(x)的零点。
情境引入
画出下列函数的图象
(1) f(x)=x-1 f(x)=x2-2x+1
(2) f(x)= f(x)=
(3) f(x)=2x -1 f(x)=log2x
思考:当函数和x轴有交点时,其交点横坐标与方程 f(x)=0的解有什么关系?
体验探究
再任意画几个函数的图象,观察其图象,看看其交点横坐标与 f(x)=0的解有什么关系?
对于函数 y=f(x),我们把使 f(x)=0 的实数x叫做函数y=f(x)的零点。
方程f(x)= 0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
一.函数零点的定义:
等价关系
★温馨提示:零点是一个实数,不是坐标。
[引例]:解方程
!
思考
(1)函数都有零点吗?
(2)什么条件下的函数必有零点?
探究3 现在有两组镜头(如图),哪
一组能说明她的行程一定曾渡河
第1组
第2组
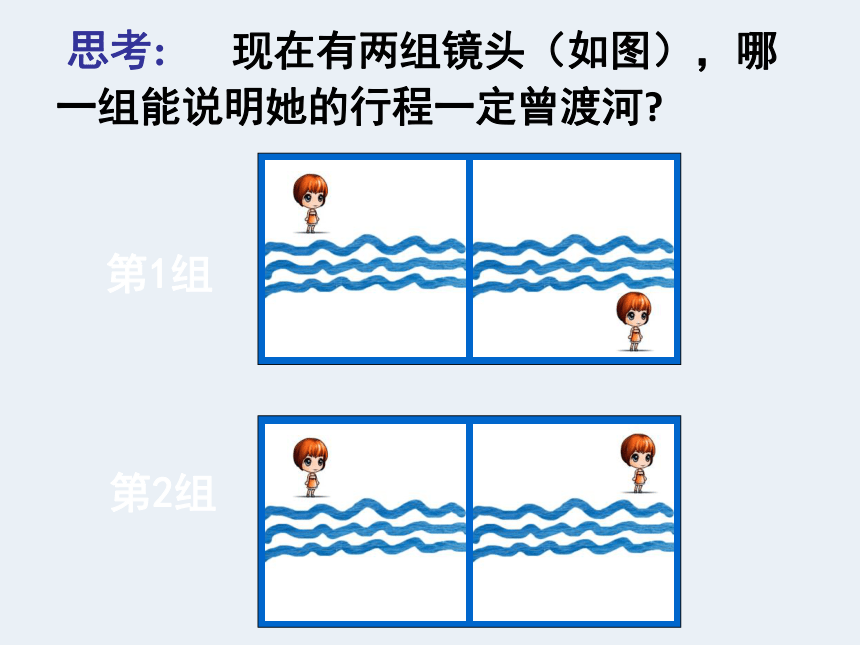
思考: 现在有两组镜头(如图),哪
一组能说明她的行程一定曾渡河
将河流抽象成x轴,将两个位置视为A、B两点。设A、B两点的横坐标分别为a、b,过A、B两点画一条连续不断的函数曲线表示她的行走路径,试连线看看?哪种情形在(a,b)内与x轴在一定会有交点?
a
b x
a
b x
a
b x
a
b x
a
b x
a
b x
观察二次函数f(x)=x2-2x-3的图象(课本P143探究):
由f(-2)>0,f(1)<0,f(2)·f(1)<0
则(-2,1)为函数f(x)=x2-2x-3
的零点所在区间.
你能找出另外一个零点所在的区间吗?
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
-2
4
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a).f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
x
y
0
a
b
.
.
二、零点存在性定理
若在给定区间[a,b]上连续,则
f(a).f(b)<0
f(x)在区间(a,b)内有零点
判断正误,若不正确,请使用函数图象举出反例
①已知函数 y=f(x) 在区间[a,b]满足f(a) ·f(b) <0,则 f(x) 在区间(a,b)内存在零点. ( )
②已知函数y=f(x) 在区间[a,b]上连续,且f(a) ·f(b) ≥0,则f(x)在区间(a,b)内没有零点. ( )
③已知函数 y=f(x)在区间[a,b]上连续,且f(a) ·f(b) <0,则
f(x)在区间(a,b)内有且仅有一个零点. ( )
三、零点存在性定理的拓宽
给定理增加什么条件时,函数在区间(a,b)上只有一个零点
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且在闭区间的两个端点上的函数值互异即f(a)·f(b)<0,且是单调函数,那么,这个函数在(a,b)内必有唯一的一个零点。
1.函数f(x)=x3+x-1在下列哪个区间有零点( )
A.(-2,-1); B.(0,1); C.(1,2); D.(2,3)
2.若函数y=5x2-7x-1在(a,b)内有零点,则f(a)·f(b)的值是( )
(A)0 (B)正数 (C)负数 (D)无法判断
B
D
练一练:
由表和图可知f(2)<0,f(3)>0,
即f(2)·f(3)<0,
∴ f(x)在(2,3)内有零点。
由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点.
[解]用计算器或计算机作出x、f(x)的对应值表和图象
-4
-1.3069
1.0986
3.3863
5.6094
7.7918
9.9459
12.0794
14.1972
[例1] 求函数f(x)=lnx+2x-6的零点个数.
1
2
3
4
5
6
7
8
9
x
f(x)
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
[另解] 求函数f(x)=lnx+2x-6的零点的个数.
作出函数y=lnx和y=6-2x的图象
[课本例1变式] 若函数f(x)为定义在R上的奇函数,且当x>0时,f(x)=lnx+2x-6.
(1)判断函数y=f(x)的零点的个数;
(2)求函数y=f(x)所有零点之和;
(3)如果R上的奇函数有零点,试问零点个数有什么特点?所有零点之和你能得出什么结论吗?偶函数呢?
6.
作业:
2.关于x的方程mx2 +2(m+3)x+2m+14=0有两实根,且一个大于4,一个小于4,求m的取值范围.
1.方程log3x+x3 =0在区间 内有无实根 为什么
4.5.1
函数的零点
与方程的解
中外历史上的方程求解
在人类用智慧架设的无数座从未知通向已知的金桥中,方程的求解是其中璀璨的一座。虽然今天我们可以从教科书中了解各式各样方程的解法,但这一切却经历了相当漫长的岁月.
约公元50~100年编成的《九章算术》给出了一次方程、二次方程和正系数三次方程的求解方法.
情境引入
中外历史上的方程求解
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法。
11世纪,北宋数学家贾宪给出了三次及三次以上的方程的解法.
情境引入
中外历史上的方程求解
国外数学家对方程求解亦有很多研究。9世纪以后,先后发现了一次、二次、三次、四次方程的求解方法。
由于实际问题的需要,我们经常需要寻求函数y=f(x)的零点。
情境引入
画出下列函数的图象
(1) f(x)=x-1 f(x)=x2-2x+1
(2) f(x)= f(x)=
(3) f(x)=2x -1 f(x)=log2x
思考:当函数和x轴有交点时,其交点横坐标与方程 f(x)=0的解有什么关系?
体验探究
再任意画几个函数的图象,观察其图象,看看其交点横坐标与 f(x)=0的解有什么关系?
对于函数 y=f(x),我们把使 f(x)=0 的实数x叫做函数y=f(x)的零点。
方程f(x)= 0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
一.函数零点的定义:
等价关系
★温馨提示:零点是一个实数,不是坐标。
[引例]:解方程
!
思考
(1)函数都有零点吗?
(2)什么条件下的函数必有零点?
探究3 现在有两组镜头(如图),哪
一组能说明她的行程一定曾渡河
第1组
第2组
思考: 现在有两组镜头(如图),哪
一组能说明她的行程一定曾渡河
将河流抽象成x轴,将两个位置视为A、B两点。设A、B两点的横坐标分别为a、b,过A、B两点画一条连续不断的函数曲线表示她的行走路径,试连线看看?哪种情形在(a,b)内与x轴在一定会有交点?
a
b x
a
b x
a
b x
a
b x
a
b x
a
b x
观察二次函数f(x)=x2-2x-3的图象(课本P143探究):
由f(-2)>0,f(1)<0,f(2)·f(1)<0
则(-2,1)为函数f(x)=x2-2x-3
的零点所在区间.
你能找出另外一个零点所在的区间吗?
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
-2
4
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a).f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
x
y
0
a
b
.
.
二、零点存在性定理
若在给定区间[a,b]上连续,则
f(a).f(b)<0
f(x)在区间(a,b)内有零点
判断正误,若不正确,请使用函数图象举出反例
①已知函数 y=f(x) 在区间[a,b]满足f(a) ·f(b) <0,则 f(x) 在区间(a,b)内存在零点. ( )
②已知函数y=f(x) 在区间[a,b]上连续,且f(a) ·f(b) ≥0,则f(x)在区间(a,b)内没有零点. ( )
③已知函数 y=f(x)在区间[a,b]上连续,且f(a) ·f(b) <0,则
f(x)在区间(a,b)内有且仅有一个零点. ( )
三、零点存在性定理的拓宽
给定理增加什么条件时,函数在区间(a,b)上只有一个零点
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且在闭区间的两个端点上的函数值互异即f(a)·f(b)<0,且是单调函数,那么,这个函数在(a,b)内必有唯一的一个零点。
1.函数f(x)=x3+x-1在下列哪个区间有零点( )
A.(-2,-1); B.(0,1); C.(1,2); D.(2,3)
2.若函数y=5x2-7x-1在(a,b)内有零点,则f(a)·f(b)的值是( )
(A)0 (B)正数 (C)负数 (D)无法判断
B
D
练一练:
由表和图可知f(2)<0,f(3)>0,
即f(2)·f(3)<0,
∴ f(x)在(2,3)内有零点。
由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点.
[解]用计算器或计算机作出x、f(x)的对应值表和图象
-4
-1.3069
1.0986
3.3863
5.6094
7.7918
9.9459
12.0794
14.1972
[例1] 求函数f(x)=lnx+2x-6的零点个数.
1
2
3
4
5
6
7
8
9
x
f(x)
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
[另解] 求函数f(x)=lnx+2x-6的零点的个数.
作出函数y=lnx和y=6-2x的图象
[课本例1变式] 若函数f(x)为定义在R上的奇函数,且当x>0时,f(x)=lnx+2x-6.
(1)判断函数y=f(x)的零点的个数;
(2)求函数y=f(x)所有零点之和;
(3)如果R上的奇函数有零点,试问零点个数有什么特点?所有零点之和你能得出什么结论吗?偶函数呢?
6.
作业:
2.关于x的方程mx2 +2(m+3)x+2m+14=0有两实根,且一个大于4,一个小于4,求m的取值范围.
1.方程log3x+x3 =0在区间 内有无实根 为什么
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
