(2022秋季新教材)六年级数学上册9.4 圆 课件(共21张PPT)
文档属性
| 名称 | (2022秋季新教材)六年级数学上册9.4 圆 课件(共21张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
2022秋 人教数学
六年级上册
圆
总复习
9
想一想,关于圆你学到了哪些知识?
圆的认识
圆的周长
圆的面积
扇形
圆的认识
圆心
半径
直径
圆的周长
圆的面积
圆环的面积
圆
扇形
C=2r
S=r2
S=r2
1.圆的认识
圆心O 确定圆的位置
半径r 确定圆的大小
直径d
轴对称图形 无数条对称轴
圆的认识
r与d关系
r=d÷2
d=2r
公式
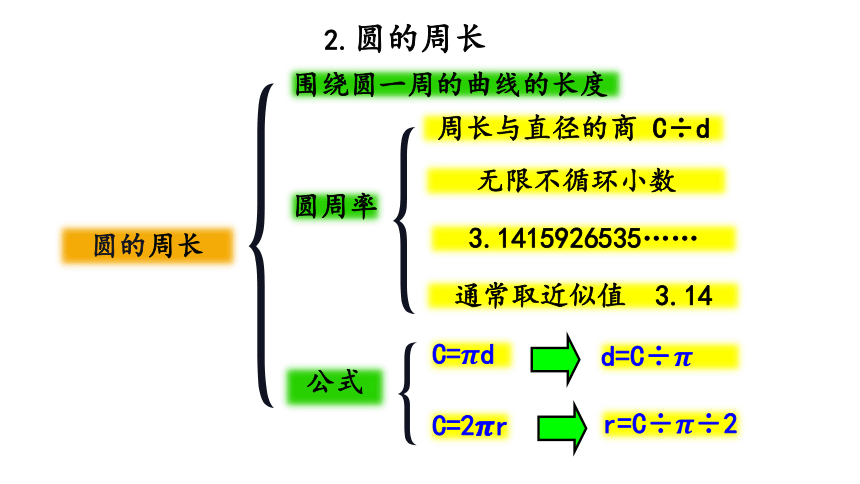
围绕圆一周的曲线的长度
圆周率
周长与直径的商 C÷d
无限不循环小数
3.1415926535……
C=d
d=C÷
通常取近似值 3.14
C=2 r
r=C÷÷2
圆的周长
2.圆的周长
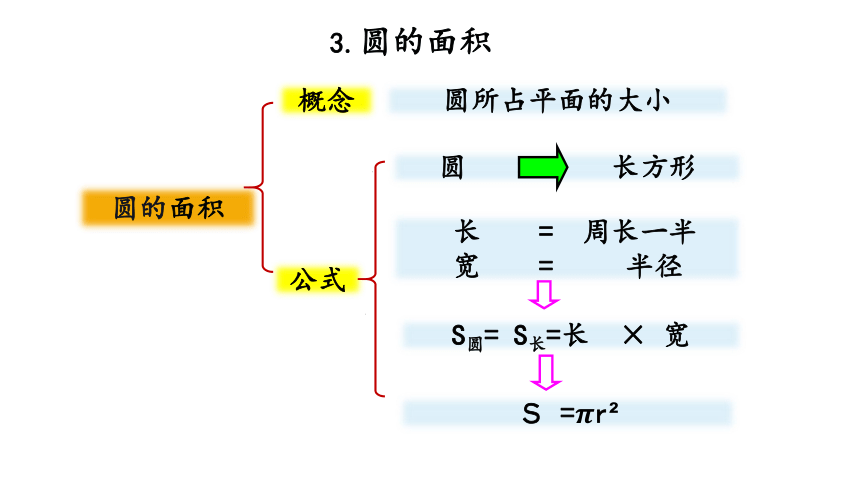
圆所占平面的大小
公式
长 = 周长一半
宽 = 半径
S =r
概念
圆 长方形
S圆= S长=长 × 宽
圆的面积
3.圆的面积
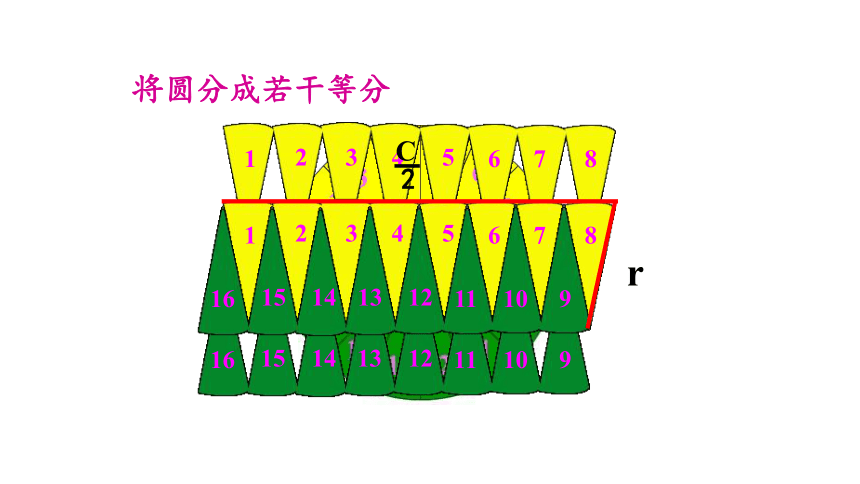
将圆分成若干等分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.圆的面积推导
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
r
C
2
将圆分成若干等分
分的份数越多,拼成的图形越接近长方形。
r
C
2
r
C
2
=
r
因为: 长方形面积 = 长 × 宽
所以: 圆 的 面 积 =r × r
S =r 2
圆环
大圆中挖小圆后剩余的部分
概念
公式
S环=R2 -r2
S环=(R2 -r2)
5.圆环
A
B
O
半径
半径
弧
扇形的定义:
一条 和 半径所围成的图形叫作扇形。
弧
经过这条弧两端的两条
顶点在圆心的角叫作圆心角
6.扇形
圆心角
跟踪训练
1.一个半圆形的养鱼池,直径4m,他的周长是( )m,
占地面积是( )m2。
2.一个圆的半径扩大了3倍,它的周长扩大了( )倍,
面积扩大了( )倍。
10.28
6.28
3
9
整圆的圆心角是
以圆为弧的扇形是所在
圆的面积的。
以圆为弧的扇形的面积。
A
B
o
90°
×=0.785(平方厘米)
1cm
如图,一个公园是圆形布局,半径长1km,圆心处设立了一坐纪念碑。公园有四个门,每两个相邻的门之间有一条直的水泥路,长约1.41km。
小湖
西门
南门
东门
纪念碑
北门
(1)这个公园的围墙有多长
求这个圆形公园的周长
C=2r=2×3.14×1=6.28(km)
答:这个公园的围墙有6.28米。
答:北门在南门的正北方向,距离南门有2km。
以南门为观测点,北门在南门的正北方向,距离南门的距离就是圆形公园直径的长度。
(2)北门在南门的什么方向?距离南门多远?
1+1=2(km)
如图,一个公园是圆形布局,半径长1km,圆心处设立了一坐纪念碑。公园有四个门,每两个相邻的门之间有一条直的水泥路,长约1.41km。
小湖
西门
南门
东门
纪念碑
大圆的面积-小圆面积=陆地面积
3.14×12-3.14×0.22=3.0144(km2)
答:这个公园的陆地面积是3.0144平方千米。
(3)如果公园里有一个半径为0.2km的圆形小湖,这个公园的陆地面积是多少平方千米?
如图,一个公园是圆形布局,半径长1km,圆心处设立了一坐纪念碑。公园有四个门,每两个相邻的门之间有一条直的水泥路,长约1.41km。
小湖
西门
南门
东门
纪念碑
一辆自行车车轮的外直径是0.8m,它每分钟转动150周,照这样的速度,这辆自行车1小时所行的路程是多少千米?
1时=60分
3.14×0.8×150×60
=22608(m)
=22.608(千米)
答:这辆自行车1小时所行的路程是22.608千米。
杜师傅要把一张边长为1.2m的方桌面改成一张最大的圆桌面,锯下的边角料的面积有多少平方米?
=1.22-3.14×0.62
=1.44-1.1304
=0.3096(平方米)
答:锯下的边角料的面积有0.3096平方米。
1.2×1.2-3.14 ×(1.2÷2)2
求出下列涂色部分的面积
大扇形的面积:3.14×10 ÷4=78.5cm
小扇形的面积:3.14×8 ÷4=50.24cm
涂色部分面积:78.5-50.24=28.26cm
2022秋 人教数学
六年级上册
圆
总复习
9
想一想,关于圆你学到了哪些知识?
圆的认识
圆的周长
圆的面积
扇形
圆的认识
圆心
半径
直径
圆的周长
圆的面积
圆环的面积
圆
扇形
C=2r
S=r2
S=r2
1.圆的认识
圆心O 确定圆的位置
半径r 确定圆的大小
直径d
轴对称图形 无数条对称轴
圆的认识
r与d关系
r=d÷2
d=2r
公式
围绕圆一周的曲线的长度
圆周率
周长与直径的商 C÷d
无限不循环小数
3.1415926535……
C=d
d=C÷
通常取近似值 3.14
C=2 r
r=C÷÷2
圆的周长
2.圆的周长
圆所占平面的大小
公式
长 = 周长一半
宽 = 半径
S =r
概念
圆 长方形
S圆= S长=长 × 宽
圆的面积
3.圆的面积
将圆分成若干等分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.圆的面积推导
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
1
2
3
4
5
6
7
8
16
15
14
13
12
11
10
9
r
C
2
将圆分成若干等分
分的份数越多,拼成的图形越接近长方形。
r
C
2
r
C
2
=
r
因为: 长方形面积 = 长 × 宽
所以: 圆 的 面 积 =r × r
S =r 2
圆环
大圆中挖小圆后剩余的部分
概念
公式
S环=R2 -r2
S环=(R2 -r2)
5.圆环
A
B
O
半径
半径
弧
扇形的定义:
一条 和 半径所围成的图形叫作扇形。
弧
经过这条弧两端的两条
顶点在圆心的角叫作圆心角
6.扇形
圆心角
跟踪训练
1.一个半圆形的养鱼池,直径4m,他的周长是( )m,
占地面积是( )m2。
2.一个圆的半径扩大了3倍,它的周长扩大了( )倍,
面积扩大了( )倍。
10.28
6.28
3
9
整圆的圆心角是
以圆为弧的扇形是所在
圆的面积的。
以圆为弧的扇形的面积。
A
B
o
90°
×=0.785(平方厘米)
1cm
如图,一个公园是圆形布局,半径长1km,圆心处设立了一坐纪念碑。公园有四个门,每两个相邻的门之间有一条直的水泥路,长约1.41km。
小湖
西门
南门
东门
纪念碑
北门
(1)这个公园的围墙有多长
求这个圆形公园的周长
C=2r=2×3.14×1=6.28(km)
答:这个公园的围墙有6.28米。
答:北门在南门的正北方向,距离南门有2km。
以南门为观测点,北门在南门的正北方向,距离南门的距离就是圆形公园直径的长度。
(2)北门在南门的什么方向?距离南门多远?
1+1=2(km)
如图,一个公园是圆形布局,半径长1km,圆心处设立了一坐纪念碑。公园有四个门,每两个相邻的门之间有一条直的水泥路,长约1.41km。
小湖
西门
南门
东门
纪念碑
大圆的面积-小圆面积=陆地面积
3.14×12-3.14×0.22=3.0144(km2)
答:这个公园的陆地面积是3.0144平方千米。
(3)如果公园里有一个半径为0.2km的圆形小湖,这个公园的陆地面积是多少平方千米?
如图,一个公园是圆形布局,半径长1km,圆心处设立了一坐纪念碑。公园有四个门,每两个相邻的门之间有一条直的水泥路,长约1.41km。
小湖
西门
南门
东门
纪念碑
一辆自行车车轮的外直径是0.8m,它每分钟转动150周,照这样的速度,这辆自行车1小时所行的路程是多少千米?
1时=60分
3.14×0.8×150×60
=22608(m)
=22.608(千米)
答:这辆自行车1小时所行的路程是22.608千米。
杜师傅要把一张边长为1.2m的方桌面改成一张最大的圆桌面,锯下的边角料的面积有多少平方米?
=1.22-3.14×0.62
=1.44-1.1304
=0.3096(平方米)
答:锯下的边角料的面积有0.3096平方米。
1.2×1.2-3.14 ×(1.2÷2)2
求出下列涂色部分的面积
大扇形的面积:3.14×10 ÷4=78.5cm
小扇形的面积:3.14×8 ÷4=50.24cm
涂色部分面积:78.5-50.24=28.26cm
