有理数的乘法[上学期]
图片预览





文档简介
课件27张PPT。有理数的乘法
新民初中 冯海云教学目标 掌握有理数乘法的运算法则
能较熟练地进行有理数的乘法运算
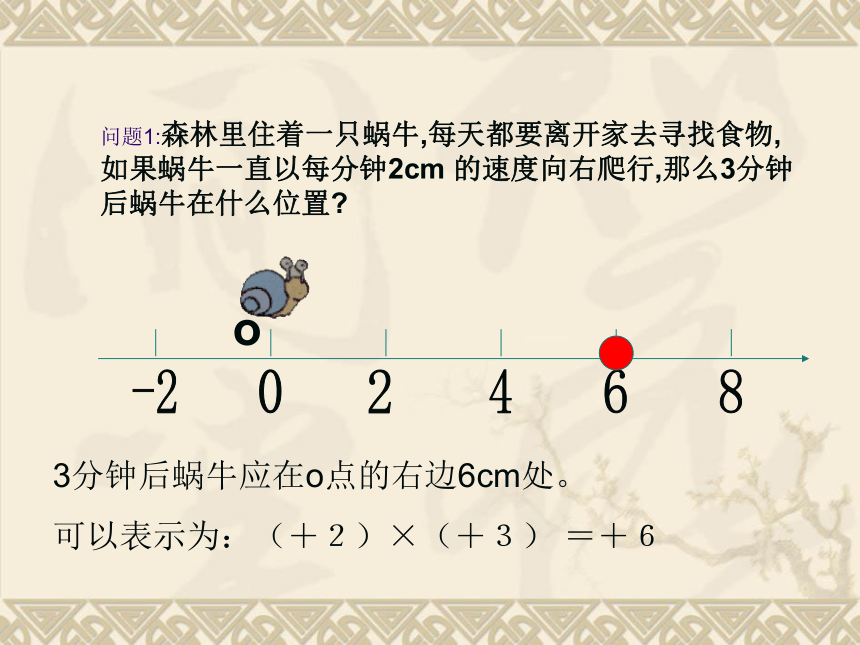
一、创设情境商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?二、导入新课问题1:森林里住着一只蜗牛,每天都要离开家去寻找食物,如果蜗牛一直以每分钟2cm 的速度向右爬行,那么3分钟后蜗牛在什么位置?3分钟后蜗牛应在o点的右边6cm处。
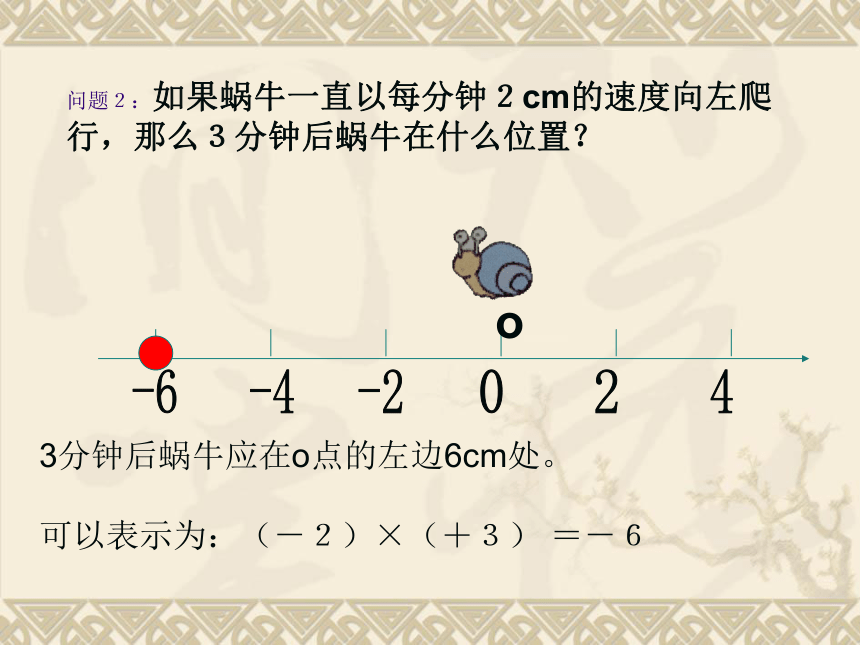
可以表示为:(+2)×(+3) =+6o问题2:如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟后蜗牛在什么位置?3分钟后蜗牛应在o点的左边6cm处。
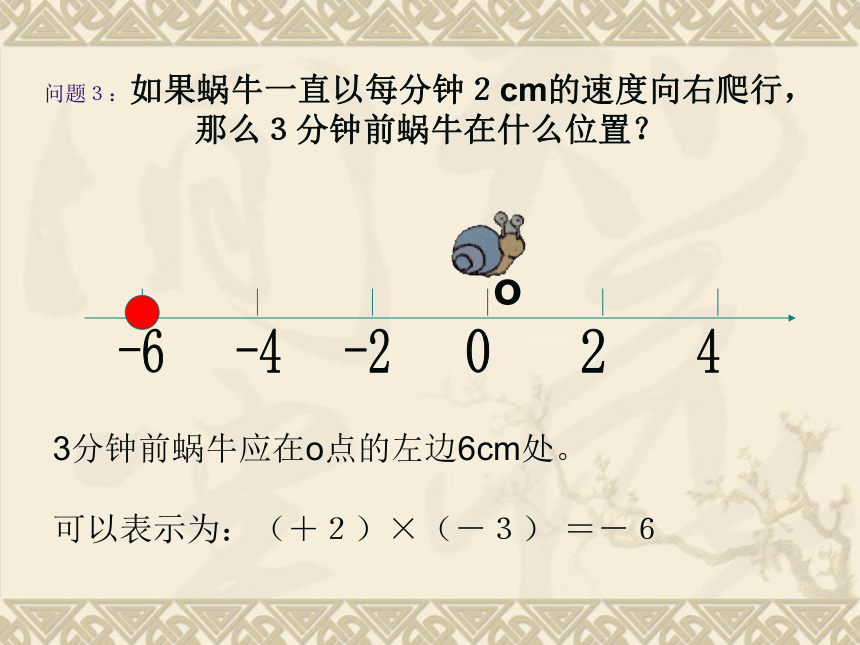
可以表示为:(-2)×(+3) =-6o问题3:如果蜗牛一直以每分钟2cm的速度向右爬行,那么3分钟前蜗牛在什么位置?3分钟前蜗牛应在o点的左边6cm处。
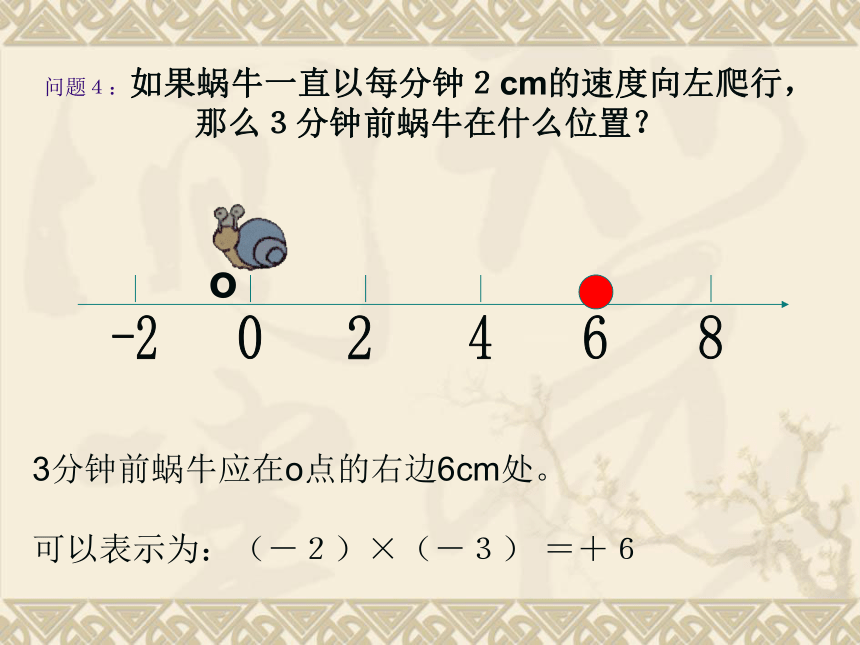
可以表示为:(+2)×(-3) =-6o问题4:如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟前蜗牛在什么位置?3分钟前蜗牛应在o点的右边6cm处。
可以表示为:(-2)×(-3) =+6o三、观察与归纳观察这四个式子:
(+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
根据你对有理数乘法的思考,总结填空:
正数乘正数积为__数:负数乘负数积为__数:
负数乘正数积为__数:正数乘负数积为__数:
乘积的绝对值等于各乘数绝对值的_____。正正负负积?思考:当一个因数为0时,积是多少?(同号得正)(异号得负)有理数乘法法则两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。四、形成技能先阅读,再填空:
(-5)x(-3)………….同号两数相乘
(-5)x(-3)=+( )…………得正
5 x 3= 15………………把绝对值相乘
所以 (-5) x (-3)= 15填空: (-7)x 4……………____________________
(-7)x 4 = -( )……………_____________________
x 4 = 28…………………_______________
所以 (-7)x 4 = _____________________
异号两数相乘得负把绝对值相乘-28例 题 解 析例1 计算:
(1) 9×6 ; (2) (?9)×6 ;
解:(1) 9×6 (2) (?9)×6
= +(9×6) = ?(9×6)
=54 ; = ? 54;(3) 3 × (-4)(4)(-3) × (-4)= 12; 求解中的第一步是 ;确定积的符号 第二步
是 ;绝对值相乘(3) 3 ×(-4) (4)(-3)×(-4) = ?(3 ×4) = +(3×4) = ? 12;
运算方法:
有理数相乘,先确定积的______,再
确定积的_______。符号绝对值 五、自主训练例1 计算:
(1)5 x (-3)
(2)(-4) x 6
(3)(-7) x(-9)
(4)0.5 x 0.7
(5)(-3)×(- )
(6)(- )×4
=-15=+63=-24=+0.35=+=-2 巩固练习:
计算:(1)6×(-9)
(2)(-4)×6
(3)(-6)×(-1)
(4)(-6)×0
(5) ×(- )
(6)(- )× 例2 计算:
(1) ×2 ; (2) (- ) × ( -2 ) 。 解:(1) ×2 = 1(2)(- )×(-2)=1 观察上面两题有何特点?总结:有理数中仍然有:乘积是1的两个数互为倒数.?数a(a≠0)的倒数是什么?(a≠0时,a的倒数是 )说出下列各数的倒数:
1,-1, ,- ,5,-5, ,-思考:
若a小于0,b大于0,则ab____0.
若a小于0,b小于0,则ab_____0.
(3)若ab大于0,则a、b应满足什么条件?
(4)若ab小于0,则a、b应满足什么条件?六、巩固提高例3 用正负数表示气温的变化量,上升为正,下降为负。登山队攀登一座山峰,每登高1千米,气温的变化量为-6℃,攀登3千米后,气温有什么变化?解:(-6)×3=-18
答:气温下降18℃。 商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?解:规定:提价为正,降价为负
(-5)×60=-300
答:销售额减少300元.归纳总结学习了有理数乘法法则
学会了有理数乘法运算的方法与技巧
知道了有理数中仍然有:乘积是1的两个数互为倒数做一做1.书面作业:教科书47页习题1.2.3.
2.预习作业:预习教科书37页至43页.
并想一想:
(1) 三个或三个以上不等于零的有理数相乘时,积的符号如何决定?
(2)在有理数运算中,乘法的交换律,结合律以及分配律还成立吗?谢谢大家!
新民初中 冯海云教学目标 掌握有理数乘法的运算法则
能较熟练地进行有理数的乘法运算
一、创设情境商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?二、导入新课问题1:森林里住着一只蜗牛,每天都要离开家去寻找食物,如果蜗牛一直以每分钟2cm 的速度向右爬行,那么3分钟后蜗牛在什么位置?3分钟后蜗牛应在o点的右边6cm处。
可以表示为:(+2)×(+3) =+6o问题2:如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟后蜗牛在什么位置?3分钟后蜗牛应在o点的左边6cm处。
可以表示为:(-2)×(+3) =-6o问题3:如果蜗牛一直以每分钟2cm的速度向右爬行,那么3分钟前蜗牛在什么位置?3分钟前蜗牛应在o点的左边6cm处。
可以表示为:(+2)×(-3) =-6o问题4:如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟前蜗牛在什么位置?3分钟前蜗牛应在o点的右边6cm处。
可以表示为:(-2)×(-3) =+6o三、观察与归纳观察这四个式子:
(+2)×(+3)=+6 (-2)×(-3)=+6
(-2)×(+3)=-6 (+2)×(-3)=-6
根据你对有理数乘法的思考,总结填空:
正数乘正数积为__数:负数乘负数积为__数:
负数乘正数积为__数:正数乘负数积为__数:
乘积的绝对值等于各乘数绝对值的_____。正正负负积?思考:当一个因数为0时,积是多少?(同号得正)(异号得负)有理数乘法法则两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。四、形成技能先阅读,再填空:
(-5)x(-3)………….同号两数相乘
(-5)x(-3)=+( )…………得正
5 x 3= 15………………把绝对值相乘
所以 (-5) x (-3)= 15填空: (-7)x 4……………____________________
(-7)x 4 = -( )……………_____________________
x 4 = 28…………………_______________
所以 (-7)x 4 = _____________________
异号两数相乘得负把绝对值相乘-28例 题 解 析例1 计算:
(1) 9×6 ; (2) (?9)×6 ;
解:(1) 9×6 (2) (?9)×6
= +(9×6) = ?(9×6)
=54 ; = ? 54;(3) 3 × (-4)(4)(-3) × (-4)= 12; 求解中的第一步是 ;确定积的符号 第二步
是 ;绝对值相乘(3) 3 ×(-4) (4)(-3)×(-4) = ?(3 ×4) = +(3×4) = ? 12;
运算方法:
有理数相乘,先确定积的______,再
确定积的_______。符号绝对值 五、自主训练例1 计算:
(1)5 x (-3)
(2)(-4) x 6
(3)(-7) x(-9)
(4)0.5 x 0.7
(5)(-3)×(- )
(6)(- )×4
=-15=+63=-24=+0.35=+=-2 巩固练习:
计算:(1)6×(-9)
(2)(-4)×6
(3)(-6)×(-1)
(4)(-6)×0
(5) ×(- )
(6)(- )× 例2 计算:
(1) ×2 ; (2) (- ) × ( -2 ) 。 解:(1) ×2 = 1(2)(- )×(-2)=1 观察上面两题有何特点?总结:有理数中仍然有:乘积是1的两个数互为倒数.?数a(a≠0)的倒数是什么?(a≠0时,a的倒数是 )说出下列各数的倒数:
1,-1, ,- ,5,-5, ,-思考:
若a小于0,b大于0,则ab____0.
若a小于0,b小于0,则ab_____0.
(3)若ab大于0,则a、b应满足什么条件?
(4)若ab小于0,则a、b应满足什么条件?六、巩固提高例3 用正负数表示气温的变化量,上升为正,下降为负。登山队攀登一座山峰,每登高1千米,气温的变化量为-6℃,攀登3千米后,气温有什么变化?解:(-6)×3=-18
答:气温下降18℃。 商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数量的商品相比,销售额有什么变化?解:规定:提价为正,降价为负
(-5)×60=-300
答:销售额减少300元.归纳总结学习了有理数乘法法则
学会了有理数乘法运算的方法与技巧
知道了有理数中仍然有:乘积是1的两个数互为倒数做一做1.书面作业:教科书47页习题1.2.3.
2.预习作业:预习教科书37页至43页.
并想一想:
(1) 三个或三个以上不等于零的有理数相乘时,积的符号如何决定?
(2)在有理数运算中,乘法的交换律,结合律以及分配律还成立吗?谢谢大家!
