人教版七年级上册1.5.1 乘方课件(共18张PPT)
文档属性
| 名称 | 人教版七年级上册1.5.1 乘方课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 208.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 08:33:39 | ||
图片预览





文档简介
(共18张PPT)
1.5.1.1 有理数的乘方
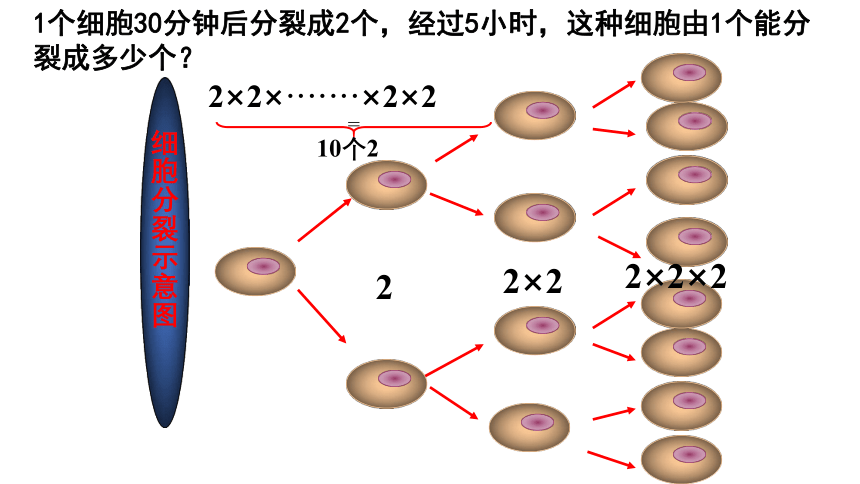
细胞分裂示意图
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
2×2×·······×2×2
=
10个2
乘方的意义
求n个相同因数的积的运算叫做乘方.
读作a的n次方,乘方的结果叫做幂,
即an叫做幂.
3. an也读作a的n次幂,a叫做底数,n叫做指数,如:(-3)2读作负3的2次方,或负3的2次幂,底数是-3,指数是2,9叫做它的幂.
说明:
(1)一个数可以看作自身的一次方,如2就是21,m就是m1,指数1通常省略不写.
(2)指数是2时也读作平方,指数是3时也读作立方,如a2读作a的平方,a3读作a的立方.
(3)当底数是负数或分数时,底数要加括号,以免造成误解,如底数是-11,指数是2时,写作(-11)2,不能写成-112,-112表示112的相反数;又如底数是 ,指数是2时,写作 ,不能写成 , 表示22比3.
乘方的法则及性质
有理数的乘方运算是利用有理数的乘法运算进行的,有下列运算规律:
(1)负数的奇次幂是负数,负数的偶次幂是正数.
(2)正数的任何次幂都是正数,0的任何正整数次幂都是0.
注意:根据有理数乘方的法则可知:
(1)互为相反数的两个数的奇次幂仍然互为相反数,即:若a+b=0,则a2n+1+b2n+1=0(n为自然数).
(2)互为相反数的两个数的偶次幂相等,即:若a+b=0,则a2n=b2n(n为自然数).
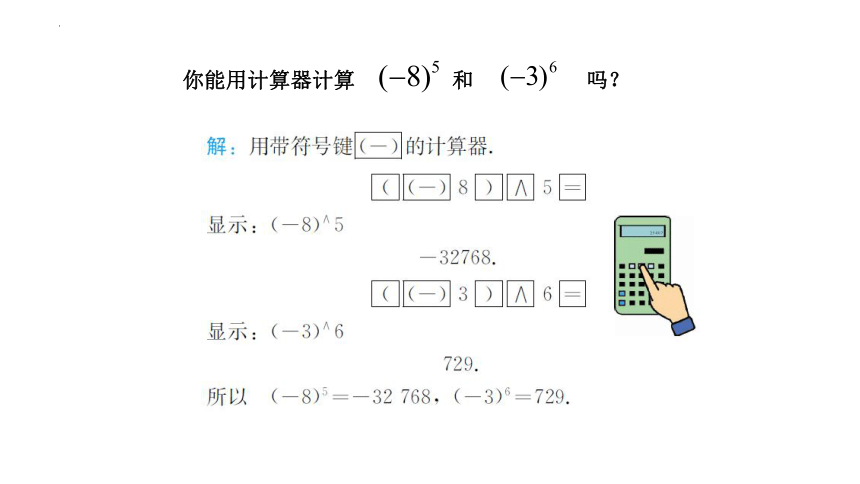
你能用计算器计算 和 吗?
例题
把下列乘方写成乘法的形式:
1.
2.
3.
练习
(-1)的偶数次幂为___
(-1)的奇数次幂为___
1的任何次幂为____
0的正整数次幂为____
有理数的混合运算
做有理数的混合运算时,应注意以下运算顺序:
①先乘方,再乘除,最后加减;
②同级运算,从左到右进行;
③如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
通常把六种基本的代数运算分成三级.
第一级运算是加和减,
第二级运算是乘和除,
第三级运算是乘方和开方.
运算顺序的规定是:先算高级运算,再算低级运算,同级运算在一起,按从左到右的顺序进行.
在进行混合运算时,除遵守以上原则外,还需注意灵活使用运算律,使运算准确而快捷.
小结
1. 有理数的乘方:
(1)定义:求n个 因数的积的运算,叫做乘方.
(2)乘方的结果叫做 . 相同因数的个数叫 ,相同因数叫 .
(3)乘方的符号法则:正数的任何次幂都是 ;负数的奇数次幂是 ,偶数次幂是 ,除 以外,任何数的0次幂都是 .
2. 有理数混合运算法则:先算 ,再算 ,最后算 ,有括号就先算 .
(-7)×(-7)×(-7)
4
6. 下列幂中为负数的是( )
A.23
B.(-2)2
C.(-2)5
D.023
7. -23等于( )
A.-6
B.6
C.-8
D.8
C
C
9.计算:
(1)(-1)5; (2)(-1)20;
(3)63; (4)(-7)3;
解:-1
解:1
解:216
解:-343
8.一个数的5次幂是负数,则这个数的4次幂是____.
正数
解:-0.008
解:1 000
解:1 000 000
解:-16
解:8
10.用计算器计算:
(1)(-12)3; (2)134;
(3)4.63; (4)(-5.8)4.
解:-1 728
解:28 561
解:97.336
解:1 131.649 6
11.一个有理数的平方( )
A.一定是正数
B.一定是负数
C.一定不是正数
D.一定不是负数
12.一个数的立方等于它本身,这个数是( )
A.1
B.-1,1
C.0
D.-1,1,0
D
D
13.下列说法中,正确的有( )
①任何小于1的有理数的平方都比1小;
②任何有理数的平方都是正数;
③互为相反数的两数的平方相等;
④平方得225的数只有15.
A.0个
B.1个
C.2个
D.3个
B
14.某种细菌在培养过程中,细菌每半小时分裂一次(由一个分裂两个),经过两个小时,这种细菌由1个可分裂为( )
A.4个
B.8个
C.16个
D.32个
C
15.一个数的平方等于它本身,则这个数是____.
0,1
1.5.1.1 有理数的乘方
细胞分裂示意图
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
2×2×·······×2×2
=
10个2
乘方的意义
求n个相同因数的积的运算叫做乘方.
读作a的n次方,乘方的结果叫做幂,
即an叫做幂.
3. an也读作a的n次幂,a叫做底数,n叫做指数,如:(-3)2读作负3的2次方,或负3的2次幂,底数是-3,指数是2,9叫做它的幂.
说明:
(1)一个数可以看作自身的一次方,如2就是21,m就是m1,指数1通常省略不写.
(2)指数是2时也读作平方,指数是3时也读作立方,如a2读作a的平方,a3读作a的立方.
(3)当底数是负数或分数时,底数要加括号,以免造成误解,如底数是-11,指数是2时,写作(-11)2,不能写成-112,-112表示112的相反数;又如底数是 ,指数是2时,写作 ,不能写成 , 表示22比3.
乘方的法则及性质
有理数的乘方运算是利用有理数的乘法运算进行的,有下列运算规律:
(1)负数的奇次幂是负数,负数的偶次幂是正数.
(2)正数的任何次幂都是正数,0的任何正整数次幂都是0.
注意:根据有理数乘方的法则可知:
(1)互为相反数的两个数的奇次幂仍然互为相反数,即:若a+b=0,则a2n+1+b2n+1=0(n为自然数).
(2)互为相反数的两个数的偶次幂相等,即:若a+b=0,则a2n=b2n(n为自然数).
你能用计算器计算 和 吗?
例题
把下列乘方写成乘法的形式:
1.
2.
3.
练习
(-1)的偶数次幂为___
(-1)的奇数次幂为___
1的任何次幂为____
0的正整数次幂为____
有理数的混合运算
做有理数的混合运算时,应注意以下运算顺序:
①先乘方,再乘除,最后加减;
②同级运算,从左到右进行;
③如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
通常把六种基本的代数运算分成三级.
第一级运算是加和减,
第二级运算是乘和除,
第三级运算是乘方和开方.
运算顺序的规定是:先算高级运算,再算低级运算,同级运算在一起,按从左到右的顺序进行.
在进行混合运算时,除遵守以上原则外,还需注意灵活使用运算律,使运算准确而快捷.
小结
1. 有理数的乘方:
(1)定义:求n个 因数的积的运算,叫做乘方.
(2)乘方的结果叫做 . 相同因数的个数叫 ,相同因数叫 .
(3)乘方的符号法则:正数的任何次幂都是 ;负数的奇数次幂是 ,偶数次幂是 ,除 以外,任何数的0次幂都是 .
2. 有理数混合运算法则:先算 ,再算 ,最后算 ,有括号就先算 .
(-7)×(-7)×(-7)
4
6. 下列幂中为负数的是( )
A.23
B.(-2)2
C.(-2)5
D.023
7. -23等于( )
A.-6
B.6
C.-8
D.8
C
C
9.计算:
(1)(-1)5; (2)(-1)20;
(3)63; (4)(-7)3;
解:-1
解:1
解:216
解:-343
8.一个数的5次幂是负数,则这个数的4次幂是____.
正数
解:-0.008
解:1 000
解:1 000 000
解:-16
解:8
10.用计算器计算:
(1)(-12)3; (2)134;
(3)4.63; (4)(-5.8)4.
解:-1 728
解:28 561
解:97.336
解:1 131.649 6
11.一个有理数的平方( )
A.一定是正数
B.一定是负数
C.一定不是正数
D.一定不是负数
12.一个数的立方等于它本身,这个数是( )
A.1
B.-1,1
C.0
D.-1,1,0
D
D
13.下列说法中,正确的有( )
①任何小于1的有理数的平方都比1小;
②任何有理数的平方都是正数;
③互为相反数的两数的平方相等;
④平方得225的数只有15.
A.0个
B.1个
C.2个
D.3个
B
14.某种细菌在培养过程中,细菌每半小时分裂一次(由一个分裂两个),经过两个小时,这种细菌由1个可分裂为( )
A.4个
B.8个
C.16个
D.32个
C
15.一个数的平方等于它本身,则这个数是____.
0,1
