第二章 直角三角形的边角关系单元检测题(含答案)
文档属性
| 名称 | 第二章 直角三角形的边角关系单元检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 688.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 16:36:00 | ||
图片预览



文档简介
直角三角形的边角关系章末检测
一、选择题(每小题3分,共36分)
1. 下列三角函数的值是的是( )
A. cos30° B. tan30° C. cos45° D. sin30°
2. 若用我们数学课本上采用的科学计算器计算sin42°16′,按键顺序正确的是( )
A.
B.
C.
D.
3. 如图,∠ABC=∠BDA=90°,下列线段比值等于cosA的是( )
A. B. C. D.
第3题图 第5题图 第6题图
4. 已知锐角α,且sinα=cos38°,则α=( )
A. 38° B. 62° C. 52° D. 72°
5. 在台风来临之前,有关部门用钢管加固树木(如图),固定点A离地面的高度AC=m,钢管与地面所成角∠ABC=α,那么钢管AB的长为( )
A. B. m·sinα C. m·cosα D.
6. 如图,在3×4的正方形网格图中.小正方形的边长为1,△ABC的顶点均在格点上,下列关于△ABC的说法中,不正确的是( )
A. 是直角三角形 B. tanB=1 C. 面积为5 D. BC边上的高为
7. 角α,β满足0°<α<β<45°,下列是关于角α,β的命题,其中错误的是( )
A. 0<sinα< B. 0<tanβ<1 C. cosβ<sinα D. sinβ<cosα
8. 如图,在Rt△ABC中,∠C=90°,cosB=,点D在BC边上,CD=AC,AB=26,则BD的长为( )
A. 10 B. 12 C. 14 D. 16
第8题图 第11题图 第12题图
9. 点P的坐标为(6,2),A是x轴正半轴上一点,O为原点,则cos∠AOP的值为( )
A. 3 B. C. D.
10. 田远同学从家里沿北偏西60°方向走100 m到商场购买文具,再从商场向正南方向走200 m到学校,田远同学的家离学校( )
A. 50 m B. 100 m C. 150 m D. 100 m
11. 如图为2021年北京冬奥会“雪飞天”滑雪大跳台赛道. 若点D与点A的水平距离DE=a米,水平赛道BC=b米,赛道AB,CD的坡角均为θ,则点A的高AE为( )
A. (a﹣b)tanθ米 B. 米
C. (a﹣b)sinθ米 D. (a-b)cosθ米
12. 如图,在△ABC中,∠ABC=90°,tan∠BAC=,AD=2,BD=4,连接CD,则CD长的最大值是( )
A. B. C. D.
二、填空题(每小题3分,共18分)
13. 在△ABC中,∠A,∠B为锐角,且|tanA-1|+=0,则∠C= °.
14. 已知Rt△ABC中,∠C=90°,如果BC∶AB=3∶4,那么cosA的值为 .
15. 如图,在△ABC中,AB=,tan∠ABC=,AC=2,则BC= .
第15题图 第16题图
16. 如图是我们经常看到的一种折叠桌子,它是由下面的支架AD,BC与桌面AB构成.若OA=OB=OC=
OD= cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是________cm.
第17题图 第18题图
17. 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sin α= .
18. 因东坡文化远近闻名的遗爱湖公园,“国庆黄金周”期间,游人络绎不绝.现有一艘游船载着游客在遗爱湖中游览,如图,当船在A处时,船上游客发现岸上P1处的临皋亭和P2处的遗爱亭都在东北方向;当游船向正东方向行驶600 m到达B处时,游客发现遗爱亭在北偏西15°方向;当游船继续向正东方向行驶400 m到达C处时,游客发现临皋亭在北偏西60°方向,则临皋亭P1处与遗爱亭P2处之间的距离为 m. (结果精确到到1 m;参考数据:≈1.414,≈2.449)
三、解答题(共66分)
19.(6分)在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边. 若c=,b=,求∠B.
20.(8分)如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5. 求∠A的三个三角函数值.
第20题图
21.(8分)如图,在△ABC中,AB=AC=,sinB=.
(1)求边BC的长度;
(2)求cosA的值.
第21题图
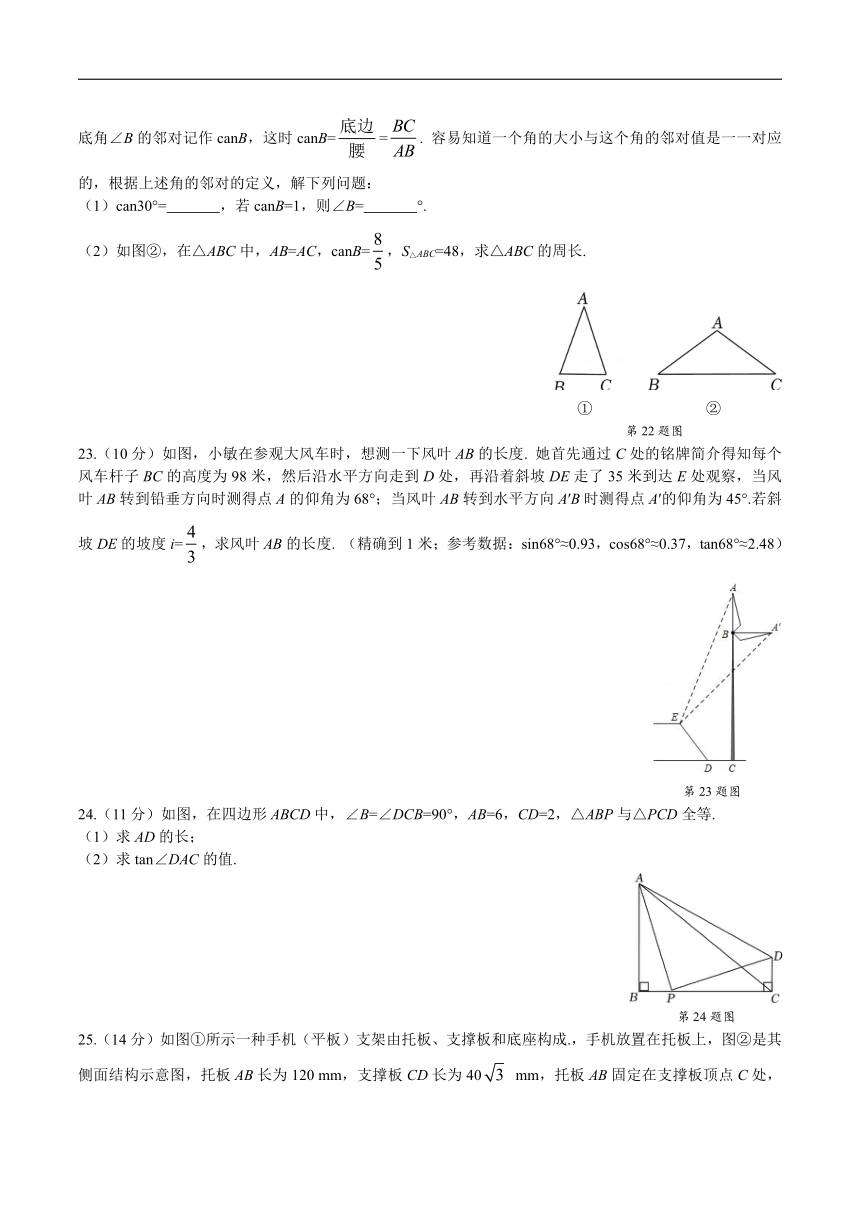
22.(9分)我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图①,在△ABC中,AB=AC,底角∠B的邻对记作canB,这时canB==. 容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题:
(1)can30°= ,若canB=1,则∠B= °.
(2)如图②,在△ABC中,AB=AC,canB=,S△ABC=48,求△ABC的周长.
① ②
第22题图
23.(10分)如图,小敏在参观大风车时,想测一下风叶AB的长度. 她首先通过C处的铭牌简介得知每个风车杆子BC的高度为98米,然后沿水平方向走到D处,再沿着斜坡DE走了35米到达E处观察,当风叶AB转到铅垂方向时测得点A的仰角为68°;当风叶AB转到水平方向A′B时测得点A′的仰角为45°.若斜坡DE的坡度i=,求风叶AB的长度. (精确到1米;参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48)
第23题图
24.(11分)如图,在四边形ABCD中,∠B=∠DCB=90°,AB=6,CD=2,△ABP与△PCD全等.
(1)求AD的长;
(2)求tan∠DAC的值.
第24题图
25.(14分)如图①所示一种手机(平板)支架由托板、支撑板和底座构成.,手机放置在托板上,图②是其侧面结构示意图,托板AB长为120 mm,支撑板CD长为40 mm,托板AB固定在支撑板顶点C处,且CB=40 mm,托板AB可绕点C转动,支撑板CD可绕点D转动,∠CDE=60°.
(1)当∠DCB=75°时,求点A到直线DE的距离;
(2)为了观看舒适,如图③,把(1)中∠DCB=75°调整为90°,然后将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.
① ② ③
第25题图
参考答案:
直角三角形的边角关系章末检测
一、1. B 2. C 3. C 4. C 5. D 6. C 7. C 8. C 9. B 10. B 11. A
12. B 提示:如图,在AD的下方作Rt△ADT,使得∠ADT=90°,DT=1,连接CT,则AT=,tan∠DAT==.因为tan∠BAC==,所以∠DAT=∠BAC.所以∠DAB=∠TAC,cos∠DAT=cos∠BAC,即=.所以△DAB∽△TAC.所以==.所以CT=.因为CD≤DT+CT,所以CD的最大值为.
二、13. 75 14. 15. 16. 60 17.
18. 152 提示:作P1M⊥AC于点M.设P1M=x m,则AM=P1M=x m,MC=P1M·tan60°=x m.因为AC=AM+CM=AB+BC,所以x+x=1000,解得x=.所以AM=P1M= m.所以P1A=AM=
m.作BN⊥AP2于点N.因为∠P2AB=45°,∠P2BA=75°,所以
∠P2=60°,BN= AN=AB·sin45°= m.所以P2N==×=
m.所以P1P2=P2N-P1N= P2N-(P1A- AN)=≈152 m.
三、19. 解:(1)因为sinB===,所以∠B=45°.
20. sinA=,cosA=,tanA=.
21. 解:(1)过点A作AD⊥BC,垂足为D.
在Rt△ABD中,AD=AB sinB=×=1.
所以BD===.
因为AB=AC,AD⊥BC,所以BC=2BD=2.
(2)过点C作CE⊥AB,垂足为E.
因为△ABC的面积为AB CE=BC AD,所以CE=2×1,解得CE=.
所以AE===.
在Rt△AEC中,cos∠CAE==.
22. 解:(1) 60
(2)过点A作AD⊥BC,垂足为D.
因为canB==,所以设BC=8x,AB=AC=5x.
因为AB=AC,AD⊥BC,所以BD=BC=4x.
所以AD==3x.
因为S△ABC=48,所以BC AD=48,即×8x×3x=48,解得x=±2(负值舍去).
所以x=2.所以AB=AC=10,BC=16.
所以△ABC的周长为AB+AC+BC=36.
23. 解:如图,过点E作EF⊥CD于点F,作EG⊥AC于点G,A′H⊥EG于点H,则四边形A′BGH,CGEF是矩形.
因为斜坡DE的坡度i==,可设EF=4k,DF=3k,所以DE==5k=35,解得k=7.所以EF=28,DF=21.
所以A′H=BG=BG-CG= BG-EF=70.
因为∠A′EH=45°,所以EH==70.
设AB=A′B=x米,则EG=(70﹣x)米,AG=(70+x)米.
在Rt△AEG中,tan∠AEG==tan68°,即≈2.48,解得x≈30.
所以风叶AB的长度约为30米.
24. 解:(1)因为△ABP≌△PCD,所以AB=PC=6,BP=CD=2,AP=PD,∠APB=∠PDC.
因为∠PCD=90°,所以∠CPD+∠PDC=90°.
所以∠CPD+∠APB=90°.所以∠APD=90°.
所以PD==2.
所以AD===4.
(2)过点D作DH⊥AC于点H.
在Rt△ABC中,∠B=90°,AB=6,BC=BP+PC=8,所以AC==10.
因为AB∥CD,所以∠CAB=∠DCH.
因为∠B=∠CHD=90°,所以△ABC∽△CHD.
所以==,即==,解得CH=,DH=.
所以AH=AC-CH=.
所以tan∠DAC==.
25. 解:(1)如图,过点C作CN⊥DE于点N,过点A作AM⊥DE,交ED的延长线于点M,过点C作CF⊥AM于点F,则四边形CFMN是矩形.所以FM=CN,∠FCN=90°.
在Rt△CDN中,所以CN=CD sin∠CDN=40×=60,所以FM=60.
因为∠CND=90°,所以∠DCN=90°-∠CDN=30°.
因为∠DCB=75°,所以∠BCN=∠DCB-∠DCN=45°.
所以∠ACF=180°-∠FCN-∠BCN=45°.
在Rt△AFC中,AF=AC sin45°=80×=40.
所以AM=AF+FM=40+60.
所以点A到直线DE的距离为(40+60)mm.
① ②
第25题图
(2)为了观看舒适,将CD绕点D顺时针旋转后如图②所示.
在Rt△DCB中,tan∠CDB==.
所以∠CDB=30°.
所以CD旋转的角度为60°-30°=30°.
第12题图
第18题图
第23题图
第 6 页 共 9 页
一、选择题(每小题3分,共36分)
1. 下列三角函数的值是的是( )
A. cos30° B. tan30° C. cos45° D. sin30°
2. 若用我们数学课本上采用的科学计算器计算sin42°16′,按键顺序正确的是( )
A.
B.
C.
D.
3. 如图,∠ABC=∠BDA=90°,下列线段比值等于cosA的是( )
A. B. C. D.
第3题图 第5题图 第6题图
4. 已知锐角α,且sinα=cos38°,则α=( )
A. 38° B. 62° C. 52° D. 72°
5. 在台风来临之前,有关部门用钢管加固树木(如图),固定点A离地面的高度AC=m,钢管与地面所成角∠ABC=α,那么钢管AB的长为( )
A. B. m·sinα C. m·cosα D.
6. 如图,在3×4的正方形网格图中.小正方形的边长为1,△ABC的顶点均在格点上,下列关于△ABC的说法中,不正确的是( )
A. 是直角三角形 B. tanB=1 C. 面积为5 D. BC边上的高为
7. 角α,β满足0°<α<β<45°,下列是关于角α,β的命题,其中错误的是( )
A. 0<sinα< B. 0<tanβ<1 C. cosβ<sinα D. sinβ<cosα
8. 如图,在Rt△ABC中,∠C=90°,cosB=,点D在BC边上,CD=AC,AB=26,则BD的长为( )
A. 10 B. 12 C. 14 D. 16
第8题图 第11题图 第12题图
9. 点P的坐标为(6,2),A是x轴正半轴上一点,O为原点,则cos∠AOP的值为( )
A. 3 B. C. D.
10. 田远同学从家里沿北偏西60°方向走100 m到商场购买文具,再从商场向正南方向走200 m到学校,田远同学的家离学校( )
A. 50 m B. 100 m C. 150 m D. 100 m
11. 如图为2021年北京冬奥会“雪飞天”滑雪大跳台赛道. 若点D与点A的水平距离DE=a米,水平赛道BC=b米,赛道AB,CD的坡角均为θ,则点A的高AE为( )
A. (a﹣b)tanθ米 B. 米
C. (a﹣b)sinθ米 D. (a-b)cosθ米
12. 如图,在△ABC中,∠ABC=90°,tan∠BAC=,AD=2,BD=4,连接CD,则CD长的最大值是( )
A. B. C. D.
二、填空题(每小题3分,共18分)
13. 在△ABC中,∠A,∠B为锐角,且|tanA-1|+=0,则∠C= °.
14. 已知Rt△ABC中,∠C=90°,如果BC∶AB=3∶4,那么cosA的值为 .
15. 如图,在△ABC中,AB=,tan∠ABC=,AC=2,则BC= .
第15题图 第16题图
16. 如图是我们经常看到的一种折叠桌子,它是由下面的支架AD,BC与桌面AB构成.若OA=OB=OC=
OD= cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是________cm.
第17题图 第18题图
17. 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sin α= .
18. 因东坡文化远近闻名的遗爱湖公园,“国庆黄金周”期间,游人络绎不绝.现有一艘游船载着游客在遗爱湖中游览,如图,当船在A处时,船上游客发现岸上P1处的临皋亭和P2处的遗爱亭都在东北方向;当游船向正东方向行驶600 m到达B处时,游客发现遗爱亭在北偏西15°方向;当游船继续向正东方向行驶400 m到达C处时,游客发现临皋亭在北偏西60°方向,则临皋亭P1处与遗爱亭P2处之间的距离为 m. (结果精确到到1 m;参考数据:≈1.414,≈2.449)
三、解答题(共66分)
19.(6分)在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边. 若c=,b=,求∠B.
20.(8分)如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5. 求∠A的三个三角函数值.
第20题图
21.(8分)如图,在△ABC中,AB=AC=,sinB=.
(1)求边BC的长度;
(2)求cosA的值.
第21题图
22.(9分)我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图①,在△ABC中,AB=AC,底角∠B的邻对记作canB,这时canB==. 容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题:
(1)can30°= ,若canB=1,则∠B= °.
(2)如图②,在△ABC中,AB=AC,canB=,S△ABC=48,求△ABC的周长.
① ②
第22题图
23.(10分)如图,小敏在参观大风车时,想测一下风叶AB的长度. 她首先通过C处的铭牌简介得知每个风车杆子BC的高度为98米,然后沿水平方向走到D处,再沿着斜坡DE走了35米到达E处观察,当风叶AB转到铅垂方向时测得点A的仰角为68°;当风叶AB转到水平方向A′B时测得点A′的仰角为45°.若斜坡DE的坡度i=,求风叶AB的长度. (精确到1米;参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48)
第23题图
24.(11分)如图,在四边形ABCD中,∠B=∠DCB=90°,AB=6,CD=2,△ABP与△PCD全等.
(1)求AD的长;
(2)求tan∠DAC的值.
第24题图
25.(14分)如图①所示一种手机(平板)支架由托板、支撑板和底座构成.,手机放置在托板上,图②是其侧面结构示意图,托板AB长为120 mm,支撑板CD长为40 mm,托板AB固定在支撑板顶点C处,且CB=40 mm,托板AB可绕点C转动,支撑板CD可绕点D转动,∠CDE=60°.
(1)当∠DCB=75°时,求点A到直线DE的距离;
(2)为了观看舒适,如图③,把(1)中∠DCB=75°调整为90°,然后将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.
① ② ③
第25题图
参考答案:
直角三角形的边角关系章末检测
一、1. B 2. C 3. C 4. C 5. D 6. C 7. C 8. C 9. B 10. B 11. A
12. B 提示:如图,在AD的下方作Rt△ADT,使得∠ADT=90°,DT=1,连接CT,则AT=,tan∠DAT==.因为tan∠BAC==,所以∠DAT=∠BAC.所以∠DAB=∠TAC,cos∠DAT=cos∠BAC,即=.所以△DAB∽△TAC.所以==.所以CT=.因为CD≤DT+CT,所以CD的最大值为.
二、13. 75 14. 15. 16. 60 17.
18. 152 提示:作P1M⊥AC于点M.设P1M=x m,则AM=P1M=x m,MC=P1M·tan60°=x m.因为AC=AM+CM=AB+BC,所以x+x=1000,解得x=.所以AM=P1M= m.所以P1A=AM=
m.作BN⊥AP2于点N.因为∠P2AB=45°,∠P2BA=75°,所以
∠P2=60°,BN= AN=AB·sin45°= m.所以P2N==×=
m.所以P1P2=P2N-P1N= P2N-(P1A- AN)=≈152 m.
三、19. 解:(1)因为sinB===,所以∠B=45°.
20. sinA=,cosA=,tanA=.
21. 解:(1)过点A作AD⊥BC,垂足为D.
在Rt△ABD中,AD=AB sinB=×=1.
所以BD===.
因为AB=AC,AD⊥BC,所以BC=2BD=2.
(2)过点C作CE⊥AB,垂足为E.
因为△ABC的面积为AB CE=BC AD,所以CE=2×1,解得CE=.
所以AE===.
在Rt△AEC中,cos∠CAE==.
22. 解:(1) 60
(2)过点A作AD⊥BC,垂足为D.
因为canB==,所以设BC=8x,AB=AC=5x.
因为AB=AC,AD⊥BC,所以BD=BC=4x.
所以AD==3x.
因为S△ABC=48,所以BC AD=48,即×8x×3x=48,解得x=±2(负值舍去).
所以x=2.所以AB=AC=10,BC=16.
所以△ABC的周长为AB+AC+BC=36.
23. 解:如图,过点E作EF⊥CD于点F,作EG⊥AC于点G,A′H⊥EG于点H,则四边形A′BGH,CGEF是矩形.
因为斜坡DE的坡度i==,可设EF=4k,DF=3k,所以DE==5k=35,解得k=7.所以EF=28,DF=21.
所以A′H=BG=BG-CG= BG-EF=70.
因为∠A′EH=45°,所以EH==70.
设AB=A′B=x米,则EG=(70﹣x)米,AG=(70+x)米.
在Rt△AEG中,tan∠AEG==tan68°,即≈2.48,解得x≈30.
所以风叶AB的长度约为30米.
24. 解:(1)因为△ABP≌△PCD,所以AB=PC=6,BP=CD=2,AP=PD,∠APB=∠PDC.
因为∠PCD=90°,所以∠CPD+∠PDC=90°.
所以∠CPD+∠APB=90°.所以∠APD=90°.
所以PD==2.
所以AD===4.
(2)过点D作DH⊥AC于点H.
在Rt△ABC中,∠B=90°,AB=6,BC=BP+PC=8,所以AC==10.
因为AB∥CD,所以∠CAB=∠DCH.
因为∠B=∠CHD=90°,所以△ABC∽△CHD.
所以==,即==,解得CH=,DH=.
所以AH=AC-CH=.
所以tan∠DAC==.
25. 解:(1)如图,过点C作CN⊥DE于点N,过点A作AM⊥DE,交ED的延长线于点M,过点C作CF⊥AM于点F,则四边形CFMN是矩形.所以FM=CN,∠FCN=90°.
在Rt△CDN中,所以CN=CD sin∠CDN=40×=60,所以FM=60.
因为∠CND=90°,所以∠DCN=90°-∠CDN=30°.
因为∠DCB=75°,所以∠BCN=∠DCB-∠DCN=45°.
所以∠ACF=180°-∠FCN-∠BCN=45°.
在Rt△AFC中,AF=AC sin45°=80×=40.
所以AM=AF+FM=40+60.
所以点A到直线DE的距离为(40+60)mm.
① ②
第25题图
(2)为了观看舒适,将CD绕点D顺时针旋转后如图②所示.
在Rt△DCB中,tan∠CDB==.
所以∠CDB=30°.
所以CD旋转的角度为60°-30°=30°.
第12题图
第18题图
第23题图
第 6 页 共 9 页
