第三章 二次函数单元检测题(含答案)
图片预览


文档简介
二次函数章末检测
一、选择题(每小题3分,共36分)
1. 在下列关于x的函数中,是二次函数的是( )
A. y=-3x+5 B. y=x(4x-3) C. y=2(x+4)2-2x2 D. y=
2. 二次函数y=-3(x+2)2-5的图象的顶点坐标是( )
A. (2,5) B. (2,-5) C. (-2,5) D. (-2,-5)
3. 函数y=的自变量x的取值范围是( )
A. x≥1 B. x≥1且x≠2 C. x>1 D. 任意实数
4. 二次函数y=x2图象可以看作是由y=x2+4x+4的图象平移得到的,下列正确的叙述是( )
A. 向左平移2个单位 B. 向右平移2个单位
C. 向上平移4个单位 D. 向下平移4个单位
5. 已知(-3,y1),(-2.5,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则( )
A. y3<y2<y1 B. y2<y3<y1 C. y3<y1<y2 D. y1<y3<y2
6. 新冠病毒抗原检测方便快捷,一般15-20分钟可出结果.小明用下列表格表示新冠病毒抗原检测试剂盒总价w与试剂盒数量n之间的函数关系:
试剂盒数量n(盒) … 3 4 5 6 7 8 …
总价w(元) … 45 60 75 90 105 120 …
根据表格数据,下列说法不正确的是( )
A. 在这个变化过程中,n是自变量,w是因变量
B. n每增加1盒,w增加15元
C. 总价w与试剂盒数量n的关系式为w=15n
D. 按照表格表示的规律,试剂盒数量为100盒时,总价为1200元
7. 如图,小明以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯,杯体轴截面ABC是抛物线y=x2+5的一部分,则杯口的口径AC为( )
A. 7 B. 8 C. 9 D. 10
第7题图 第8题图
8. 小苏和小林在一条300米的直道上进行慢跑,先到终点的同学会在跑道的尽头等待.在整个过程中,小苏和小林之间的距离y(米)与跑步时间t(秒)的对应关系如图所示,下列命题:①小苏和小林在第19秒时相遇;②小苏和小林之间的最大距离为30米;③先到终点的同学用时58秒跑完了全程;④先到终点的同学用时50秒跑完了全程.其中正确的是( )
A. 仅①② B. ①②③ C. ①②④ D. 仅②④
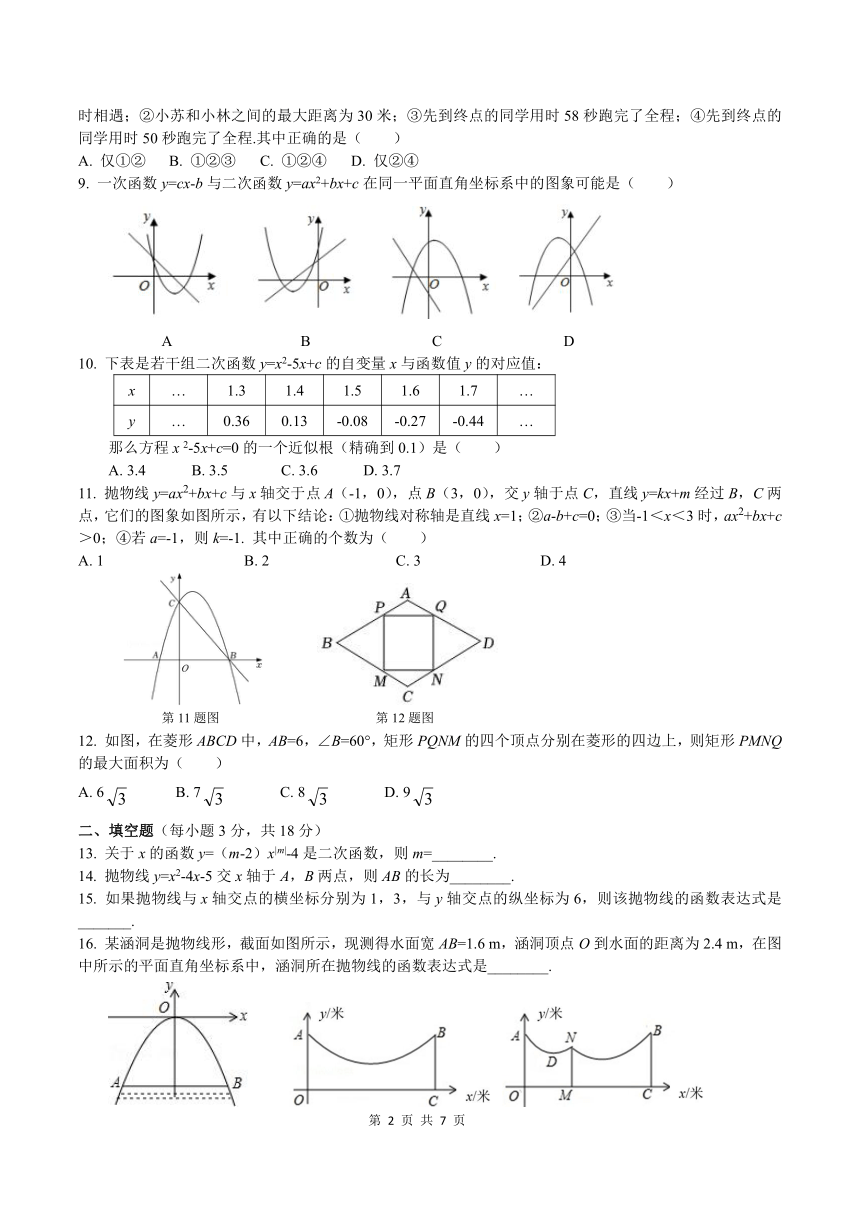
9. 一次函数y=cx-b与二次函数y=ax2+bx+c在同一平面直角坐标系中的图象可能是( )
A B C D
10. 下表是若干组二次函数y=x2-5x+c的自变量x与函数值y的对应值:
x … 1.3 1.4 1.5 1.6 1.7 …
y … 0.36 0.13 -0.08 -0.27 -0.44 …
那么方程x 2-5x+c=0的一个近似根(精确到0.1)是( )
A. 3.4 B. 3.5 C. 3.6 D. 3.7
11. 抛物线y=ax2+bx+c与x轴交于点A(-1,0),点B(3,0),交y轴于点C,直线y=kx+m经过B,C两点,它们的图象如图所示,有以下结论:①抛物线对称轴是直线x=1;②a-b+c=0;③当-1<x<3时,ax2+bx+c>0;④若a=-1,则k=-1. 其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
第11题图 第12题图
12. 如图,在菱形ABCD中,AB=6,∠B=60°,矩形PQNM的四个顶点分别在菱形的四边上,则矩形PMNQ的最大面积为( )
A. 6 B. 7 C. 8 D. 9
二、填空题(每小题3分,共18分)
13. 关于x的函数y=(m-2)x|m|-4是二次函数,则m=________.
14. 抛物线y=x2-4x-5交x轴于A,B两点,则AB的长为________.
15. 如果抛物线与x轴交点的横坐标分别为1,3,与y轴交点的纵坐标为6,则该抛物线的函数表达式是_______.
16. 某涵洞是抛物线形,截面如图所示,现测得水面宽AB=1.6 m,涵洞顶点O到水面的距离为2.4 m,在图中所示的平面直角坐标系中,涵洞所在抛物线的函数表达式是________.
第16题图 第18题图
17. 当k取实数时,抛物线y=3(x-k-1)2+k2+2的顶点所在的函数图象的表达式为_____________.
18. AO,BC是两根垂直于地面的立柱,且长度相等. 在两根立柱之间悬挂着一根绳子,建立图①所示的平面直角坐标系,绳子形如抛物线y=x2-x+4的图象. 因实际需要,在OA与BC间用一根高为2.5m的立柱MN将绳子撑起,若立柱MN到OA的水平距离为3 m,MN左侧抛物线的最低点D与MN的水平距离为1 m,则点D到地面的距离为 m.
三、解答题(共66分)
19.(6分)已知二次函数的表达式为y=﹣x2+x+2.
(1)求该二次函数图象的开口方向、对称轴和顶点坐标;
(2)当x在什么范围内时,y随x的增大而增大?
20.(8分)已知二次函数y=x2+2x-3.
(1)用配方法把这个二次函数化成y=a(x-h)2+k的形式;
(2)在所给的平面直角坐标系中,画出这个二次函数的图象;
(3)当-4≤x≤0时,结合图象直接写出y的取值范围.
第20题图
21.(8分)已知抛物线y=2x2+bx+c经过A(-5,m),B(3,m),C(-2,5)三点.
(1)求抛物线的表达式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在点C处,并写出平移后抛物线的表达式.
22.(8分)某商场以每件20元的价格购进一种商品,规定这种商品每件售价不低于进价,又不高于38元,经市场调查发现:该商品每天的销售量y(件)与每件售价x(元)之间满足一次函数关系,如图所示.
(1)求y与x之间的函数关系式;
(2)设商场销售这种商品每天获利w(元),当每件商品的售价定为多少元时,每天销售利润最大?最大利润为多少?
第22题图
23.(9分)(2021 遵义)如图,抛物线y=a(x-2)2+3(a为常数且a≠0)与y轴交于点A.
(1)求该抛物线的表达式;
(2)若直线y=kx+(k≠0)与抛物线有两个交点,交点的横坐标分别为x1,x2,当x12+x22=10时,求k的值;
(3)当-4<x≤m时,y有最大值,求m的值.
第23题图
24.(11分)某公园在人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安一个喷水头,水柱从喷水头喷出到落于湖面的路径形状可以看作是抛物线的一部分. 若记水柱上某一位置与水管的水平距离为d米,与湖面的垂直高度为h米. 下表中记录了d与h的五组数据:
d(米) 0 1 2 3 4
h(米) 0.5 1.25 1.5 1.25 0.5
根据上述信息,解决以下问题:
(1)若水柱最高点距离湖面的高度为m米,则m=________;
(2)现公园想通过喷泉设立新的游玩项目,准备通过只调节水管露出湖面的高度,使得游船能从水柱下方通过. 如图所示,为避免游船被喷泉淋到,要求游船从水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米. 已知游船顶棚宽度为3米,顶棚到湖面的高度为2米,那么公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求?请通过计算说明理由(保留一位小数).
第24题图
25.(14分)抛物线y=ax2+bx-3过点A(-1,0),点B(3,0),与y轴交于点C.
(1)求抛物线的表达式及点C的坐标;
(2)如图①,设M是抛物线上的一点,若∠MAB=45°,求点M的坐标;
(3)如图②,点P在直线BC下方的抛物线上,过点P作PD⊥x轴于点D,交直线BC于点E,过点P作PF⊥BC,交BC于点F,△PEF的周长是否有最大值,若有最大值,求出此时点P的坐标;若不存在,说明理由.
① ②
第25题图
参考答案:
二次函数章末检测
一、1. B 2. D 3. B 4. B 5. C 6. D 7. C 8. C 9. D 10. B 11. D
(
第
12
题图
)12. D 提示:如图,连接AC,BD交于点O,AC分别交PQ,MN于点E,F. 因为在菱形ABCD中,BC=AB=6,∠B=60°,所以△ABC是等边三角形,∠ABD=30°.所以AC=AB=6. 因为四边形MNQP为矩形,所以PQ∥BD,PM=EF,PQ⊥AC. 所以∠APE=∠ABD=30°.设AP=a,则AE=CF=a,PE=, EF=PM=6-a.所以PQ=2PE=a. 所以S矩形PMNQ=PM PQ=(-a2+6a)=(a-3)2+9. 因为<0,所以当a=3时,矩形面积有最大值9.
二、13. -2 14. 6 15. y=2x2-8x+6 16. y=x2 17. y=x2-2x+3 18. (
第
8
题图
) (
第
8
题图
)2
三、19. 解:(1)该二次函数图象开口向下,对称轴为直线x=2,顶点坐标为(2,3).
(2)当x<2时,y随x增大而增大.
20. 解:(1)y=(x+1)2-4.
(2)画图略.
(3)-4≤y≤5.
21. 解:(1)因为抛物线y=2x2+bx+c经过A(﹣5,m),B(3,m),C(-2,5)三点,而A,B两点的纵坐标相同,所以抛物线的对称轴为直线x==-1,即=-1,解得b=4.
把C(-2,5)代入y=2x2+4x+c,得2×4+4×(-2)+c=5,解得c=5.
所以抛物线的表达式为y=2x2+4x+5.
因为y=2x2+4x+5=2(x+1)2+3,所以顶点为(-1,3).
(2)因为抛物线的顶点为(-1,3),C(-2,5),所以把抛物线向左平移一个单位,再向上平移2个单位后抛物线的顶点落在点C处.
所以平移后抛物线的表达式为y=2(x+2)2+5.
22. 解:(1)设y与x之间的函数关系式为y=kx+b(k≠0).
由题意,得解得
所以y与x的函数关系式为y=-2x+120,其中20≤x≤38.
(2)w=(x-20)(-2x+120)=-2x2+160x-2400=-2(x-40)2+800.
因为-2<0,所以当x<40时,w随x的增大而增大.
因为20≤x≤38,所以当x=38时,w取得最大值,最大值为792.
所以当每件商品的售价定为38元时,每天销售利润最大,最大利润为792元.
23. 解:解:(1)将A代入y=a(x-2)2+3,得4a+3=,解得a=.
所以该抛物线的表达式为y=(x-2)2+3.
(2)因为直线y=kx+与抛物线有两个交点,交点的横坐标分别为x1,x2,由kx+=(x-2)2+3,整理,得x2+(3k-4)x-3=0,所以Δ=(3k-4)2+12>0,x1+x2=4-3k,x1 x2=-3.所以x12+x22=(4-3k)2+6=10,解得k=或k=2.
所以k的值为2或.
(3)因为函数的对称轴为直线x=2,所以当x<2时,y随x的增大而增大.
当m<2时,y在x=m处取得最大值,即(m-2)2+3=,解得m=±(正值舍去).
当m≥2时,y在x=2处取得最大值,即=3,解得m=.
综上所述,m的值为或.
24. 解:(1)1.5
(2)根据图象可设二次函数的表达式为h=a(d-2)2+1.5,将(0,0.5)代入,得a=﹣.所以抛物线的表达式为h=﹣d2+d+0.5.
设调节后的水管喷出的抛物线的表达式为h=﹣d2+d+0.5+m.
由题意知当横坐标为2+=时,纵坐标的值不小于2+0.5=2.5,所以﹣×++0.5+m≥2.5,解得m≥1.6.
0.5+1.6=2.1(米).
所以公园应将水管露出湖面的高度至少调节到2.1米才能符合要求.
25. 解:(1)将A(-1,0),B(3,0)代入y=ax2+bx-3,得解得所以抛物线的表达式为y=x2-2x-3.
当x=0时,y=-3,所以点C的坐标为(0,-3).
(2)过点M作MN⊥x轴于点N.
设M(x0,x02-2x0-3),则N(x0,0).
因为∠MAB=45°,所以MN=AN.
所以x0+1=|x02-2x0-3|,解得x0=4或x0=2或0x=-1(与A重合,舍去).
所以点M的坐标为(4,5)或(2,-3).
(3)因为PD⊥AB,PF⊥BC,所以△EFP与△BDE为直角三角形.
设直线BC的表达式为y=kx+c,将B(3,0),C(0,-3)代入,得解得
所以直线BC的表达式为y=x-3.
由(1)知OB=OC,△OBC为等腰直角三角形,所以∠OBC=45°.
因为∠DEB=∠FEP,∠BDE=∠PFE=90°,所以∠FPE=∠DBE=45°.
所以△PEF为等腰直角三角形,所以EF∶FP∶PE=1∶1∶.
当PE存在最大值时,△PEF的周长也存在最大值.
设P(m,m2-2m-3),则E(m,m-3),所以PE=m-3-(m2-2m-3)=-m2+3m=+.
所以当m=时,△PEF的周长最大,此时,点P的坐标为.
第 7 页 共 7 页
一、选择题(每小题3分,共36分)
1. 在下列关于x的函数中,是二次函数的是( )
A. y=-3x+5 B. y=x(4x-3) C. y=2(x+4)2-2x2 D. y=
2. 二次函数y=-3(x+2)2-5的图象的顶点坐标是( )
A. (2,5) B. (2,-5) C. (-2,5) D. (-2,-5)
3. 函数y=的自变量x的取值范围是( )
A. x≥1 B. x≥1且x≠2 C. x>1 D. 任意实数
4. 二次函数y=x2图象可以看作是由y=x2+4x+4的图象平移得到的,下列正确的叙述是( )
A. 向左平移2个单位 B. 向右平移2个单位
C. 向上平移4个单位 D. 向下平移4个单位
5. 已知(-3,y1),(-2.5,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则( )
A. y3<y2<y1 B. y2<y3<y1 C. y3<y1<y2 D. y1<y3<y2
6. 新冠病毒抗原检测方便快捷,一般15-20分钟可出结果.小明用下列表格表示新冠病毒抗原检测试剂盒总价w与试剂盒数量n之间的函数关系:
试剂盒数量n(盒) … 3 4 5 6 7 8 …
总价w(元) … 45 60 75 90 105 120 …
根据表格数据,下列说法不正确的是( )
A. 在这个变化过程中,n是自变量,w是因变量
B. n每增加1盒,w增加15元
C. 总价w与试剂盒数量n的关系式为w=15n
D. 按照表格表示的规律,试剂盒数量为100盒时,总价为1200元
7. 如图,小明以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯,杯体轴截面ABC是抛物线y=x2+5的一部分,则杯口的口径AC为( )
A. 7 B. 8 C. 9 D. 10
第7题图 第8题图
8. 小苏和小林在一条300米的直道上进行慢跑,先到终点的同学会在跑道的尽头等待.在整个过程中,小苏和小林之间的距离y(米)与跑步时间t(秒)的对应关系如图所示,下列命题:①小苏和小林在第19秒时相遇;②小苏和小林之间的最大距离为30米;③先到终点的同学用时58秒跑完了全程;④先到终点的同学用时50秒跑完了全程.其中正确的是( )
A. 仅①② B. ①②③ C. ①②④ D. 仅②④
9. 一次函数y=cx-b与二次函数y=ax2+bx+c在同一平面直角坐标系中的图象可能是( )
A B C D
10. 下表是若干组二次函数y=x2-5x+c的自变量x与函数值y的对应值:
x … 1.3 1.4 1.5 1.6 1.7 …
y … 0.36 0.13 -0.08 -0.27 -0.44 …
那么方程x 2-5x+c=0的一个近似根(精确到0.1)是( )
A. 3.4 B. 3.5 C. 3.6 D. 3.7
11. 抛物线y=ax2+bx+c与x轴交于点A(-1,0),点B(3,0),交y轴于点C,直线y=kx+m经过B,C两点,它们的图象如图所示,有以下结论:①抛物线对称轴是直线x=1;②a-b+c=0;③当-1<x<3时,ax2+bx+c>0;④若a=-1,则k=-1. 其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
第11题图 第12题图
12. 如图,在菱形ABCD中,AB=6,∠B=60°,矩形PQNM的四个顶点分别在菱形的四边上,则矩形PMNQ的最大面积为( )
A. 6 B. 7 C. 8 D. 9
二、填空题(每小题3分,共18分)
13. 关于x的函数y=(m-2)x|m|-4是二次函数,则m=________.
14. 抛物线y=x2-4x-5交x轴于A,B两点,则AB的长为________.
15. 如果抛物线与x轴交点的横坐标分别为1,3,与y轴交点的纵坐标为6,则该抛物线的函数表达式是_______.
16. 某涵洞是抛物线形,截面如图所示,现测得水面宽AB=1.6 m,涵洞顶点O到水面的距离为2.4 m,在图中所示的平面直角坐标系中,涵洞所在抛物线的函数表达式是________.
第16题图 第18题图
17. 当k取实数时,抛物线y=3(x-k-1)2+k2+2的顶点所在的函数图象的表达式为_____________.
18. AO,BC是两根垂直于地面的立柱,且长度相等. 在两根立柱之间悬挂着一根绳子,建立图①所示的平面直角坐标系,绳子形如抛物线y=x2-x+4的图象. 因实际需要,在OA与BC间用一根高为2.5m的立柱MN将绳子撑起,若立柱MN到OA的水平距离为3 m,MN左侧抛物线的最低点D与MN的水平距离为1 m,则点D到地面的距离为 m.
三、解答题(共66分)
19.(6分)已知二次函数的表达式为y=﹣x2+x+2.
(1)求该二次函数图象的开口方向、对称轴和顶点坐标;
(2)当x在什么范围内时,y随x的增大而增大?
20.(8分)已知二次函数y=x2+2x-3.
(1)用配方法把这个二次函数化成y=a(x-h)2+k的形式;
(2)在所给的平面直角坐标系中,画出这个二次函数的图象;
(3)当-4≤x≤0时,结合图象直接写出y的取值范围.
第20题图
21.(8分)已知抛物线y=2x2+bx+c经过A(-5,m),B(3,m),C(-2,5)三点.
(1)求抛物线的表达式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在点C处,并写出平移后抛物线的表达式.
22.(8分)某商场以每件20元的价格购进一种商品,规定这种商品每件售价不低于进价,又不高于38元,经市场调查发现:该商品每天的销售量y(件)与每件售价x(元)之间满足一次函数关系,如图所示.
(1)求y与x之间的函数关系式;
(2)设商场销售这种商品每天获利w(元),当每件商品的售价定为多少元时,每天销售利润最大?最大利润为多少?
第22题图
23.(9分)(2021 遵义)如图,抛物线y=a(x-2)2+3(a为常数且a≠0)与y轴交于点A.
(1)求该抛物线的表达式;
(2)若直线y=kx+(k≠0)与抛物线有两个交点,交点的横坐标分别为x1,x2,当x12+x22=10时,求k的值;
(3)当-4<x≤m时,y有最大值,求m的值.
第23题图
24.(11分)某公园在人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安一个喷水头,水柱从喷水头喷出到落于湖面的路径形状可以看作是抛物线的一部分. 若记水柱上某一位置与水管的水平距离为d米,与湖面的垂直高度为h米. 下表中记录了d与h的五组数据:
d(米) 0 1 2 3 4
h(米) 0.5 1.25 1.5 1.25 0.5
根据上述信息,解决以下问题:
(1)若水柱最高点距离湖面的高度为m米,则m=________;
(2)现公园想通过喷泉设立新的游玩项目,准备通过只调节水管露出湖面的高度,使得游船能从水柱下方通过. 如图所示,为避免游船被喷泉淋到,要求游船从水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米. 已知游船顶棚宽度为3米,顶棚到湖面的高度为2米,那么公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求?请通过计算说明理由(保留一位小数).
第24题图
25.(14分)抛物线y=ax2+bx-3过点A(-1,0),点B(3,0),与y轴交于点C.
(1)求抛物线的表达式及点C的坐标;
(2)如图①,设M是抛物线上的一点,若∠MAB=45°,求点M的坐标;
(3)如图②,点P在直线BC下方的抛物线上,过点P作PD⊥x轴于点D,交直线BC于点E,过点P作PF⊥BC,交BC于点F,△PEF的周长是否有最大值,若有最大值,求出此时点P的坐标;若不存在,说明理由.
① ②
第25题图
参考答案:
二次函数章末检测
一、1. B 2. D 3. B 4. B 5. C 6. D 7. C 8. C 9. D 10. B 11. D
(
第
12
题图
)12. D 提示:如图,连接AC,BD交于点O,AC分别交PQ,MN于点E,F. 因为在菱形ABCD中,BC=AB=6,∠B=60°,所以△ABC是等边三角形,∠ABD=30°.所以AC=AB=6. 因为四边形MNQP为矩形,所以PQ∥BD,PM=EF,PQ⊥AC. 所以∠APE=∠ABD=30°.设AP=a,则AE=CF=a,PE=, EF=PM=6-a.所以PQ=2PE=a. 所以S矩形PMNQ=PM PQ=(-a2+6a)=(a-3)2+9. 因为<0,所以当a=3时,矩形面积有最大值9.
二、13. -2 14. 6 15. y=2x2-8x+6 16. y=x2 17. y=x2-2x+3 18. (
第
8
题图
) (
第
8
题图
)2
三、19. 解:(1)该二次函数图象开口向下,对称轴为直线x=2,顶点坐标为(2,3).
(2)当x<2时,y随x增大而增大.
20. 解:(1)y=(x+1)2-4.
(2)画图略.
(3)-4≤y≤5.
21. 解:(1)因为抛物线y=2x2+bx+c经过A(﹣5,m),B(3,m),C(-2,5)三点,而A,B两点的纵坐标相同,所以抛物线的对称轴为直线x==-1,即=-1,解得b=4.
把C(-2,5)代入y=2x2+4x+c,得2×4+4×(-2)+c=5,解得c=5.
所以抛物线的表达式为y=2x2+4x+5.
因为y=2x2+4x+5=2(x+1)2+3,所以顶点为(-1,3).
(2)因为抛物线的顶点为(-1,3),C(-2,5),所以把抛物线向左平移一个单位,再向上平移2个单位后抛物线的顶点落在点C处.
所以平移后抛物线的表达式为y=2(x+2)2+5.
22. 解:(1)设y与x之间的函数关系式为y=kx+b(k≠0).
由题意,得解得
所以y与x的函数关系式为y=-2x+120,其中20≤x≤38.
(2)w=(x-20)(-2x+120)=-2x2+160x-2400=-2(x-40)2+800.
因为-2<0,所以当x<40时,w随x的增大而增大.
因为20≤x≤38,所以当x=38时,w取得最大值,最大值为792.
所以当每件商品的售价定为38元时,每天销售利润最大,最大利润为792元.
23. 解:解:(1)将A代入y=a(x-2)2+3,得4a+3=,解得a=.
所以该抛物线的表达式为y=(x-2)2+3.
(2)因为直线y=kx+与抛物线有两个交点,交点的横坐标分别为x1,x2,由kx+=(x-2)2+3,整理,得x2+(3k-4)x-3=0,所以Δ=(3k-4)2+12>0,x1+x2=4-3k,x1 x2=-3.所以x12+x22=(4-3k)2+6=10,解得k=或k=2.
所以k的值为2或.
(3)因为函数的对称轴为直线x=2,所以当x<2时,y随x的增大而增大.
当m<2时,y在x=m处取得最大值,即(m-2)2+3=,解得m=±(正值舍去).
当m≥2时,y在x=2处取得最大值,即=3,解得m=.
综上所述,m的值为或.
24. 解:(1)1.5
(2)根据图象可设二次函数的表达式为h=a(d-2)2+1.5,将(0,0.5)代入,得a=﹣.所以抛物线的表达式为h=﹣d2+d+0.5.
设调节后的水管喷出的抛物线的表达式为h=﹣d2+d+0.5+m.
由题意知当横坐标为2+=时,纵坐标的值不小于2+0.5=2.5,所以﹣×++0.5+m≥2.5,解得m≥1.6.
0.5+1.6=2.1(米).
所以公园应将水管露出湖面的高度至少调节到2.1米才能符合要求.
25. 解:(1)将A(-1,0),B(3,0)代入y=ax2+bx-3,得解得所以抛物线的表达式为y=x2-2x-3.
当x=0时,y=-3,所以点C的坐标为(0,-3).
(2)过点M作MN⊥x轴于点N.
设M(x0,x02-2x0-3),则N(x0,0).
因为∠MAB=45°,所以MN=AN.
所以x0+1=|x02-2x0-3|,解得x0=4或x0=2或0x=-1(与A重合,舍去).
所以点M的坐标为(4,5)或(2,-3).
(3)因为PD⊥AB,PF⊥BC,所以△EFP与△BDE为直角三角形.
设直线BC的表达式为y=kx+c,将B(3,0),C(0,-3)代入,得解得
所以直线BC的表达式为y=x-3.
由(1)知OB=OC,△OBC为等腰直角三角形,所以∠OBC=45°.
因为∠DEB=∠FEP,∠BDE=∠PFE=90°,所以∠FPE=∠DBE=45°.
所以△PEF为等腰直角三角形,所以EF∶FP∶PE=1∶1∶.
当PE存在最大值时,△PEF的周长也存在最大值.
设P(m,m2-2m-3),则E(m,m-3),所以PE=m-3-(m2-2m-3)=-m2+3m=+.
所以当m=时,△PEF的周长最大,此时,点P的坐标为.
第 7 页 共 7 页
