第四章 投影与视图单元检测题(含答案)
文档属性
| 名称 | 第四章 投影与视图单元检测题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 351.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 16:40:07 | ||
图片预览

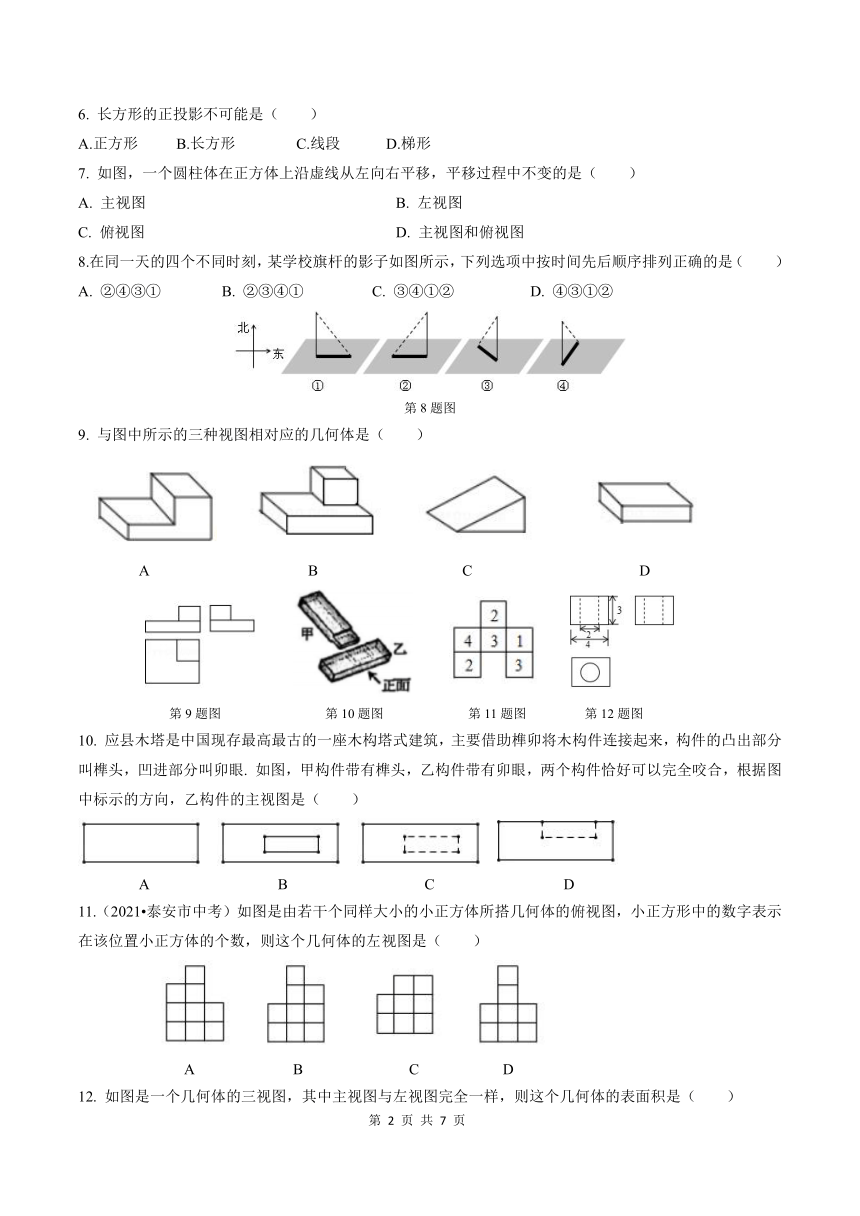
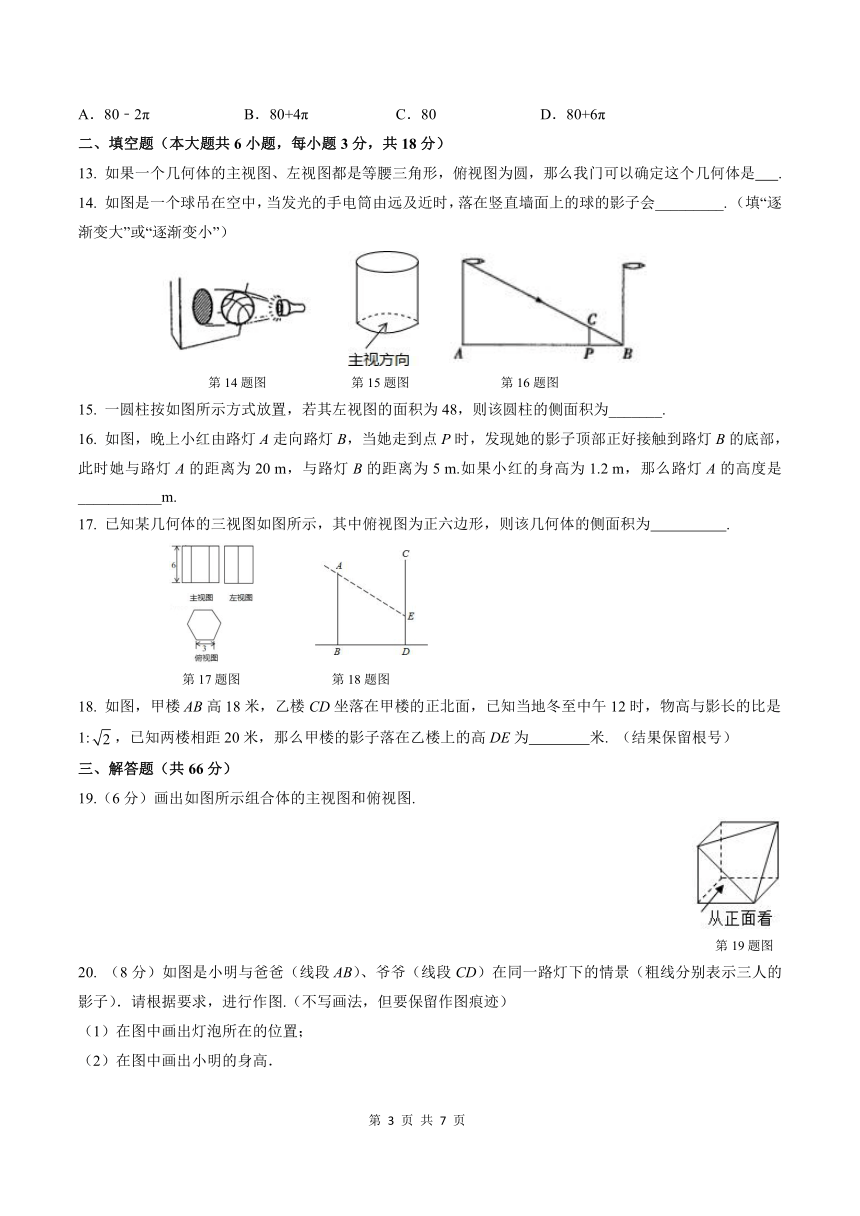
文档简介
投影与视图章末检测
选择题(本大题共12小题,每小题3分,共36分)
1.下列几何体的左视图为长方形的是( )
A B C D 第2题图
2. 三根等高的木杆竖直立在平地上,其俯视图如图所示,在某一时刻三根木杆在太阳光下的影子合理的是( )
A B C D
3. 如图是一个正三棱柱的三视图,则这个三棱柱摆放方式正确的是( )
A B C D
第3题图 第5题图 第7题图
4. 下列结论:①同一地点、同一时刻,不同物体在阳光照射下影子的方向是相同的;②不同物体在任何光线照射下影子的方向都是相同的;③同一物体在路灯照射下影子的方向与路灯的位置有关;④物体在光线照射下影子的长短仅与物体的长短有关. 其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
5. 如图,两个等直径圆柱构成如图所示的T形管道,则其俯视图是( )
A B C D
6. 长方形的正投影不可能是( )
A.正方形 B.长方形 C.线段 D.梯形
7. 如图,一个圆柱体在正方体上沿虚线从左向右平移,平移过程中不变的是( )
A. 主视图 B. 左视图
C. 俯视图 D. 主视图和俯视图
8.在同一天的四个不同时刻,某学校旗杆的影子如图所示,下列选项中按时间先后顺序排列正确的是( )
②④③① B. ②③④① C. ③④①② D. ④③①②
第8题图
9. 与图中所示的三种视图相对应的几何体是( )
A B C D
第9题图 第10题图 第11题图 第12题图
10. 应县木塔是中国现存最高最古的一座木构塔式建筑,主要借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼. 如图,甲构件带有榫头,乙构件带有卯眼,两个构件恰好可以完全咬合,根据图中标示的方向,乙构件的主视图是( )
A B C D
11.(2021 泰安市中考)如图是由若干个同样大小的小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图是( )
A B C D
12. 如图是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是( )
A.80﹣2π B.80+4π C.80 D.80+6π
二、填空题(本大题共6小题,每小题3分,共18分)
13. 如果一个几何体的主视图、左视图都是等腰三角形,俯视图为圆,那么我门可以确定这个几何体是 .
14. 如图是一个球吊在空中,当发光的手电筒由远及近时,落在竖直墙面上的球的影子会_________. (填“逐渐变大”或“逐渐变小”)
第14题图 第15题图 第16题图
15. 一圆柱按如图所示方式放置,若其左视图的面积为48,则该圆柱的侧面积为_______.
16. 如图,晚上小红由路灯A走向路灯B,当她走到点P时,发现她的影子顶部正好接触到路灯B的底部,此时她与路灯A的距离为20 m,与路灯B的距离为5 m.如果小红的身高为1.2 m,那么路灯A的高度是___________m.
17. 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为 .
第17题图 第18题图
18. 如图,甲楼AB高18米,乙楼CD坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是1:,已知两楼相距20米,那么甲楼的影子落在乙楼上的高DE为 米. (结果保留根号)
三、解答题(共66分)
19.(6分)画出如图所示组合体的主视图和俯视图.
第19题图
20. (8分)如图是小明与爸爸(线段AB)、爷爷(线段CD)在同一路灯下的情景(粗线分别表示三人的影子).请根据要求,进行作图.(不写画法,但要保留作图痕迹)
(1)在图中画出灯泡所在的位置;
(2)在图中画出小明的身高.
第20题图
21.(8分)某几何体的主视图和俯视图如图所示(单位:mm),求该几何体的体积.
第21题图
22.(9分)在平整的地面上,有若干个完全相同棱长为1的小正方体堆成一个几何图所示.
(1)若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加 个小正方体;
(2)如果需要给原来这个几何体表面喷上红漆,则喷漆面积是多少?
INCLUDEPICTURE "D:\\Documents\\WXWork\\1688852887474229\\Cache\\Image\\2021-06\\DCIM(2).jpg" \* MERGEFORMATINET INCLUDEPICTURE "D:\\Documents\\WXWork\\1688852887474229\\Cache\\Image\\2021-06\\DCIM(2).jpg" \* MERGEFORMAT INCLUDEPICTURE "D:\\Documents\\WXWork\\1688852887474229\\Cache\\Image\\2021-06\\DCIM(2).jpg" \* MERGEFORMAT
第22题图
23.(10分)小明周末到公园里散步,当他沿着一段平坦的直线跑道行走时,前方出现一棵树AC和一座景观塔BD(如图),假设小明行走到M处时正好透过树顶C看到景观塔的第5层顶端E处,此时他的视角为30°,已知树高AC=10米,景观塔BD共6层(塔顶高度和小明的身高忽略不计),每层5米.请问,小明再向前走多少米刚好看不到景观塔BD?(结果保留根号)
第23题图
(11分)如图是某几何体的三种视图.
(1)判断这个几何体的形状;
(2)若主视图的宽为8 cm,长为15 cm,左视图的宽为6 cm,求这个几何体中所有棱长的和是多少?它的表面积是多少?
第24题图
25.(14分)如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他(EF)在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH.(点C,E,G在一条直线上)
(1)请在图中画出灯光光源O的位置及小明位于点F时在这一灯光下的影长FM;(不写画法)
(2)求小明原来的速度.
第25题图
参考答案:
投影与视图章末检测
一、1. C 2. C 3. B 4. B 5. B 6. D 7. B 8. B 9. B 10. C 11. B 12. B
二、11. 圆锥 12. 逐渐变大 13. 48π 14. 6 15. 108 16.
三、19. 画图略.
20. 画图略.
21. 解:由主视图和俯视图可知,该几何体是上下两个圆柱的组合图形.
所以该几何体的体积为16×π×+4×π×=1088π(mm3).
22. 解:(1)4
(2)6×2+7×2+6+2=34.
答:喷漆面积是34.
23. 解:连接DC并延长交BM于点N.
由题意得,BE=5×5=25(米),BD=5×6=30(米).
在Rt△ACM中,AM==;在Rt△BEM中,BM==.
所以AB=BM﹣AM=﹣=.
因为AC∥BD,所以△ACN∽△BDN,所以==,即=,解得AN=.
所以MN=MA﹣NA=﹣=(米).
答:小明再向前走米刚好看不到景观塔BD.
24. 解:(1)直三棱柱.
(2)根据题意,得俯视图中直角三角形的斜边为=10(cm).
所以这个几何体中所有棱长的和为(6+8+10)×2+15×3=93(cm),
表面积为2××6×8+(6+8+10)×15=408(cm2).
25. 解:(1)灯光光源O,影长FM如图所示.
第25题图
设小明原来的速度为x 米/秒,则AD=DF=CE=2x,AM=AF-MF=2x+2x-1.2=4x-1.2,EG=FH=2×1.5x=3x,MB=AB-AM=12-(4x-1.2)=13.2-4x.
因为点C,E,G在一条直线上,CG∥AB,所以∠OCE=∠A,∠OEC=∠OMA,∠OEG=∠OMB,∠OCE=∠B.
所以△OCE∽△OAM,△OEG∽△OMB.所以,.
所以,即,解得x=1.5.
经检验,x=1.5为原分式方程的根.
答:小明原来的速度为1.5米/秒.
第 7 页 共 7 页
选择题(本大题共12小题,每小题3分,共36分)
1.下列几何体的左视图为长方形的是( )
A B C D 第2题图
2. 三根等高的木杆竖直立在平地上,其俯视图如图所示,在某一时刻三根木杆在太阳光下的影子合理的是( )
A B C D
3. 如图是一个正三棱柱的三视图,则这个三棱柱摆放方式正确的是( )
A B C D
第3题图 第5题图 第7题图
4. 下列结论:①同一地点、同一时刻,不同物体在阳光照射下影子的方向是相同的;②不同物体在任何光线照射下影子的方向都是相同的;③同一物体在路灯照射下影子的方向与路灯的位置有关;④物体在光线照射下影子的长短仅与物体的长短有关. 其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
5. 如图,两个等直径圆柱构成如图所示的T形管道,则其俯视图是( )
A B C D
6. 长方形的正投影不可能是( )
A.正方形 B.长方形 C.线段 D.梯形
7. 如图,一个圆柱体在正方体上沿虚线从左向右平移,平移过程中不变的是( )
A. 主视图 B. 左视图
C. 俯视图 D. 主视图和俯视图
8.在同一天的四个不同时刻,某学校旗杆的影子如图所示,下列选项中按时间先后顺序排列正确的是( )
②④③① B. ②③④① C. ③④①② D. ④③①②
第8题图
9. 与图中所示的三种视图相对应的几何体是( )
A B C D
第9题图 第10题图 第11题图 第12题图
10. 应县木塔是中国现存最高最古的一座木构塔式建筑,主要借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼. 如图,甲构件带有榫头,乙构件带有卯眼,两个构件恰好可以完全咬合,根据图中标示的方向,乙构件的主视图是( )
A B C D
11.(2021 泰安市中考)如图是由若干个同样大小的小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图是( )
A B C D
12. 如图是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是( )
A.80﹣2π B.80+4π C.80 D.80+6π
二、填空题(本大题共6小题,每小题3分,共18分)
13. 如果一个几何体的主视图、左视图都是等腰三角形,俯视图为圆,那么我门可以确定这个几何体是 .
14. 如图是一个球吊在空中,当发光的手电筒由远及近时,落在竖直墙面上的球的影子会_________. (填“逐渐变大”或“逐渐变小”)
第14题图 第15题图 第16题图
15. 一圆柱按如图所示方式放置,若其左视图的面积为48,则该圆柱的侧面积为_______.
16. 如图,晚上小红由路灯A走向路灯B,当她走到点P时,发现她的影子顶部正好接触到路灯B的底部,此时她与路灯A的距离为20 m,与路灯B的距离为5 m.如果小红的身高为1.2 m,那么路灯A的高度是___________m.
17. 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为 .
第17题图 第18题图
18. 如图,甲楼AB高18米,乙楼CD坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是1:,已知两楼相距20米,那么甲楼的影子落在乙楼上的高DE为 米. (结果保留根号)
三、解答题(共66分)
19.(6分)画出如图所示组合体的主视图和俯视图.
第19题图
20. (8分)如图是小明与爸爸(线段AB)、爷爷(线段CD)在同一路灯下的情景(粗线分别表示三人的影子).请根据要求,进行作图.(不写画法,但要保留作图痕迹)
(1)在图中画出灯泡所在的位置;
(2)在图中画出小明的身高.
第20题图
21.(8分)某几何体的主视图和俯视图如图所示(单位:mm),求该几何体的体积.
第21题图
22.(9分)在平整的地面上,有若干个完全相同棱长为1的小正方体堆成一个几何图所示.
(1)若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加 个小正方体;
(2)如果需要给原来这个几何体表面喷上红漆,则喷漆面积是多少?
INCLUDEPICTURE "D:\\Documents\\WXWork\\1688852887474229\\Cache\\Image\\2021-06\\DCIM(2).jpg" \* MERGEFORMATINET INCLUDEPICTURE "D:\\Documents\\WXWork\\1688852887474229\\Cache\\Image\\2021-06\\DCIM(2).jpg" \* MERGEFORMAT INCLUDEPICTURE "D:\\Documents\\WXWork\\1688852887474229\\Cache\\Image\\2021-06\\DCIM(2).jpg" \* MERGEFORMAT
第22题图
23.(10分)小明周末到公园里散步,当他沿着一段平坦的直线跑道行走时,前方出现一棵树AC和一座景观塔BD(如图),假设小明行走到M处时正好透过树顶C看到景观塔的第5层顶端E处,此时他的视角为30°,已知树高AC=10米,景观塔BD共6层(塔顶高度和小明的身高忽略不计),每层5米.请问,小明再向前走多少米刚好看不到景观塔BD?(结果保留根号)
第23题图
(11分)如图是某几何体的三种视图.
(1)判断这个几何体的形状;
(2)若主视图的宽为8 cm,长为15 cm,左视图的宽为6 cm,求这个几何体中所有棱长的和是多少?它的表面积是多少?
第24题图
25.(14分)如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他(EF)在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH.(点C,E,G在一条直线上)
(1)请在图中画出灯光光源O的位置及小明位于点F时在这一灯光下的影长FM;(不写画法)
(2)求小明原来的速度.
第25题图
参考答案:
投影与视图章末检测
一、1. C 2. C 3. B 4. B 5. B 6. D 7. B 8. B 9. B 10. C 11. B 12. B
二、11. 圆锥 12. 逐渐变大 13. 48π 14. 6 15. 108 16.
三、19. 画图略.
20. 画图略.
21. 解:由主视图和俯视图可知,该几何体是上下两个圆柱的组合图形.
所以该几何体的体积为16×π×+4×π×=1088π(mm3).
22. 解:(1)4
(2)6×2+7×2+6+2=34.
答:喷漆面积是34.
23. 解:连接DC并延长交BM于点N.
由题意得,BE=5×5=25(米),BD=5×6=30(米).
在Rt△ACM中,AM==;在Rt△BEM中,BM==.
所以AB=BM﹣AM=﹣=.
因为AC∥BD,所以△ACN∽△BDN,所以==,即=,解得AN=.
所以MN=MA﹣NA=﹣=(米).
答:小明再向前走米刚好看不到景观塔BD.
24. 解:(1)直三棱柱.
(2)根据题意,得俯视图中直角三角形的斜边为=10(cm).
所以这个几何体中所有棱长的和为(6+8+10)×2+15×3=93(cm),
表面积为2××6×8+(6+8+10)×15=408(cm2).
25. 解:(1)灯光光源O,影长FM如图所示.
第25题图
设小明原来的速度为x 米/秒,则AD=DF=CE=2x,AM=AF-MF=2x+2x-1.2=4x-1.2,EG=FH=2×1.5x=3x,MB=AB-AM=12-(4x-1.2)=13.2-4x.
因为点C,E,G在一条直线上,CG∥AB,所以∠OCE=∠A,∠OEC=∠OMA,∠OEG=∠OMB,∠OCE=∠B.
所以△OCE∽△OAM,△OEG∽△OMB.所以,.
所以,即,解得x=1.5.
经检验,x=1.5为原分式方程的根.
答:小明原来的速度为1.5米/秒.
第 7 页 共 7 页
