《同步课堂》2013-2014学年高中数学北师大版必修一模块综合检测(含解析)
文档属性
| 名称 | 《同步课堂》2013-2014学年高中数学北师大版必修一模块综合检测(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 113.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-13 20:39:37 | ||
图片预览


文档简介
模块综合检测
一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合U={1,2,3,4,5},A={1,2,3},B={2,5},则A∩(UB)=( )
A.{1,3} B.{2}
C.{2,3} D.{3}
解析:UB={1,3,4},∴A∩(UB)={1,3},故选A.
答案:A
2.函数f(x)=的定义域是( )
A.[4,+∞) B.(10,+∞)
C.(4,10)∪(10,+∞) D.[4,10)∪(10,+∞)
解析:要使函数有意义须即
解得:4≤x<10或x>10.
答案:D
3.已知幂函数f(x)=xα的部分对应值如下表,则f(x)的奇偶性是
x 1 4
f(x) 1 2
A.奇函数 B.偶函数
C.非奇非偶函数 D.既是奇函数,又是偶函数
解析:由2=4α知α=,∴f(x)=x为非奇非偶函数.
答案:C
4.设f:x→x2是集合A到集合B的映射,如果B={1,2},则A∩B一定是( )
A. B.或{1}
C.{1} D.{}
解析:令x2=1,得x=±1;令x2=2,得x=±.由映射的定义知,集合A可能含元素1,可能不含元素1,若1∈A,则A∩B={1};若1A,则A∩B=,
∴A∩B={1}或.
答案:B
5.下列大小关系正确的是( )
A.0.43<30.4<log40.3 B.0.43<log40.3<30.4
C.log40.3<0.43<30.4 D.log40.3<30.4<0.43
解析:∵log40.3<log41=0,0<0.43<0.40=1,
30.4>30=1,∴log40. 3<0.43<30.4.
答案:C
6.已知f(x)=
则f(f(2))的值是( )
A.0 B.1
C.2 D.3
解析:∵f(2)=log3(22-1)=log33=1,
∴f(f(2))=f(1)=2e1-1=2.
答案:C
7.设x0是方程ln x+x=4的解,则x0属于区间( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
解析:令y1=ln x,y2=4-x,在同一坐标系中画出它们的图像如图所示.
由图像观察可知x0∈(2,3).
答案:C
8.李明放学回家的路上,开始和同学边走边讨论问题,走得比较慢;然后他们索性停下来将问题彻底解决;最后他快速地回到了家.下列图像中与这一过程吻合得最好的是( )
解析:根据实际情况较吻合的应为D.
答案:D
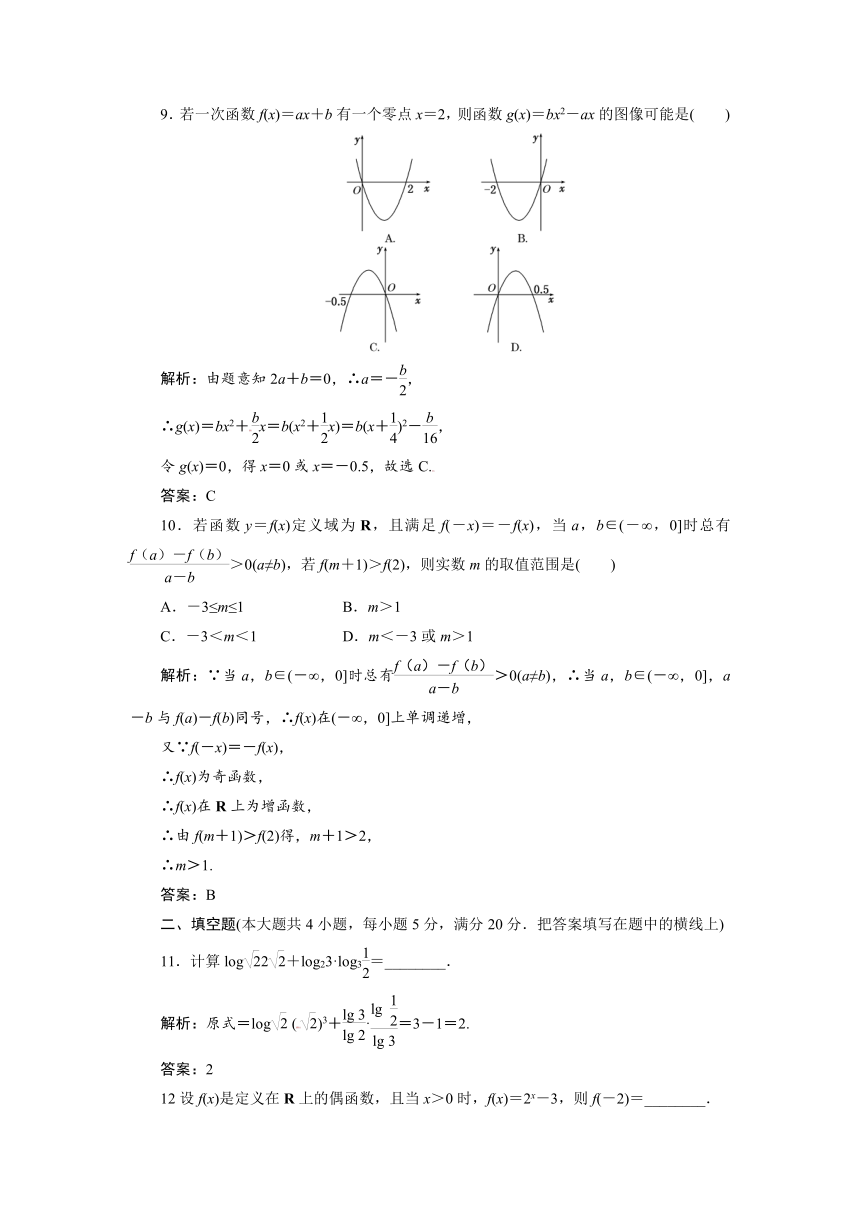
9.若一次函数f(x)=ax+b有一个零点x=2,则函数g(x)=bx2-ax的图像可能是( )
解析:由题意知2a+b=0,∴a=-,
∴g(x)=bx2+x=b(x2+x)=b(x+)2-,
令g(x)=0,得x=0或x=-0.5,故选C.
答案:C
10.若函数y=f(x)定义域为R,且满足f(-x)=-f(x),当a,b∈(-∞,0]时总有>0(a≠b),若f(m+1)>f(2),则实数m的取值范围是( )
A.-3≤m≤1 B.m>1
C.-3<m<1 D.m<-3或m>1
解析:∵当a,b∈(-∞,0]时总有>0(a≠b),∴当a,b∈(-∞,0],a-b与f(a)-f(b)同号,∴f(x)在(-∞,0]上单调递增,
又∵f(-x)=-f(x),
∴f(x)为奇函数,
∴f(x)在R上为增函数,
∴由f(m+1)>f(2)得,m+1>2,
∴m>1.
答案:B
二、填空题(本大题共4小题,每小题5分,满分20分.把答案填写在题中的横线上)
11.计算log2+log23·log3=________.
解析:原式=log ()3+·=3-1=2.
答案:2
12设f(x)是定义在R上的偶函数,且当x>0时,f(x)=2x-3,则f(-2)=________.
解析:f(-2)=f(2)=22-3=1.
答案:1
13.设函数f(x)=若f(x0)>2,则x0的取值范围是________.
解析:当x0≤0时,f(x0)=()x0>2,得x0<-1;
当x0>0时,f(x0)=x0>2,得x0>4.
∴x0的取值范围为(-∞,-1)∪(4,+∞).
答案:(-∞,-1)∪(4,+∞)
14.下列叙述:
①存在m∈R,使f(x)=(m-1)·xm2-4m+3是幂函数;
②函数y=在(-∞,-1)∪(-1,+∞)上是减函数;
③函数y=log2x+x2-2在(1,2)内只有一个零点;
④定义域内任意两个变量x1,x2,都有>0,则f(x)在定义域内是增函数.
其中正确的结论序号是________.
解析:①使f(x)=(m-1)·xm2-4m+3是幂函数,则
m-1=1,得m=2,此时f(x)=x-1,故①正确;
②减区间应为(-∞,-1)和(-1,+∞)不能合并,故②错误;
③∵f(1)=log21+1-2=-1<0,f(2)=lg 22+22-2=3>0
∴f(1) f(2)<0,且f(x)在(1,2)单调递增.故③正确;
④由已知得x1-x2与f(x1)-f(x2)同号,∴f(x)在定义域上为增函数.
综上知①③④正确.
答案:①③④
三、解答题(本大题共4小题,满分50分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分12分)已知A={x|x2+2x-8=0},B={x|log2(x2-5x+8)=1},C={x|x2-ax+a2-19=0}.
若A∩C=,B∩C≠,求a的值.
解:A={2,-4},B={2,3},
由A∩C=,知2C,-4C,
又由B∩C≠,知3∈C,
∴32-3a+a2-19=0,解得a=-2或a=5
当a=-2时,C={3,-5},满足A∩C=,
当a=5时,C={3,2},A∩C={2}≠,舍去,
∴a=-2.
16.(本小题满分12分)已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R).
(1)当函数f(x)的图像过点(-1,0),且方程f(x)=0有且只有一个根,求f(x)的表达式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(3)若F(x)=当mn<0,m+n>0,a>0,且函数f(x)为偶函数时,试判断F(m)+F(n)能否大于0
解:(1)因为f(-1)=0,所以a-b+1=0.
因为方程f(x)=0有且只有一个根,
所以Δ=b2-4a=0.
所以b2-4(b-1)=0.
即b=2,a=1.
所以f(x)=(x+1)2;
(2)因为g(x)=f(x)-kx=x2+2x+1-kx
=x2-(k-2)x+1
=(x-)2+1-.
所以当≥2或≤-2时,
即k≥6或k≤-2时,g(x)是单调函数;
(3)f(x)为偶函数,所以b=0.
所以f(x)=ax2+1.
所以F(x)=
因为mn<0,不妨设m>0,则n<0.
又因为m+n>0,所以m>-n>0.
所以|m|>|-n|.
此时F(m)+F(n)=f(m)-f(n)=am2+1-an2-1=a(m2-n2)>0.
所以F(m)+F(n)>0.
17.(本小题满分12分)如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
(1)写出y关于x的函数关系式,指出这个函数的定义域;
(2)当AE为何值时,绿地面积最大?
解:(1)S△AEH=S△CFG=x2,
S△BEF=S△DGH
=(a-x)(2-x).
∴y=S△ABCD-2S△AEH-2S△BEF
=2a-x2-(a-x)(2-x)
=-2x2+(a+2)x.
由得0<x≤2,
∴y=-2x2+(a+2)x,0<x≤2;
(2)当<2,即2<a<6时,
则x=时,y取最大值;
当≥2,即a≥6时,y=-2x2+(a+2)x,在(0,2]上是增函数,则x=2时,y取最大值2a-4
综上所述:当2<a<6时,AE=时,绿地面积取最大值;
当a≥6时 AE=2时,绿地面积取最大值2a-4.
18.(本小题满分14分)已知函数f(x)定义域为[-1,1],若对于任意的x,y∈[-1,1],都有f(x+y)=f(x)+f(y),且x>0时,有f(x)>0.
(1)证明:f(x)为奇函数;
(2)证明:f(x)在[-1,1]上是增加的;
(3)设f(1)=1,若f(x)<m-2am+2,对所有x∈[-1,1],a∈[-1,1]恒成立,求实数m的取值范围.
解:(1)令x=y=0,∴f(0)=0.
令y=-x,f(x)+f(-x)=0.
∴f(-x)=-f(x),∴f(x)为奇函数;
(2)∵f(x)是定义在[-1,1]上的奇函数,
令-1≤x1<x2≤1,
则f(x2)-f(x1)=f(x2-x1)>0
∴f(x)在[-1, 1]上是增加的;
(3)f(x)在[-1,1]上是增加的,f(x)max=f(1)=1,使f(x)<m-2am+2对所有x∈[-1,1]恒成立,只要m-2am+2>1,即m-2am+1>0.
令g(a)=m-2am+1=-2am+m+1,
要使g(a)>0时a∈[-1,1]恒成立,则
即-∴实数m的取值范围是(-,1).
一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合U={1,2,3,4,5},A={1,2,3},B={2,5},则A∩(UB)=( )
A.{1,3} B.{2}
C.{2,3} D.{3}
解析:UB={1,3,4},∴A∩(UB)={1,3},故选A.
答案:A
2.函数f(x)=的定义域是( )
A.[4,+∞) B.(10,+∞)
C.(4,10)∪(10,+∞) D.[4,10)∪(10,+∞)
解析:要使函数有意义须即
解得:4≤x<10或x>10.
答案:D
3.已知幂函数f(x)=xα的部分对应值如下表,则f(x)的奇偶性是
x 1 4
f(x) 1 2
A.奇函数 B.偶函数
C.非奇非偶函数 D.既是奇函数,又是偶函数
解析:由2=4α知α=,∴f(x)=x为非奇非偶函数.
答案:C
4.设f:x→x2是集合A到集合B的映射,如果B={1,2},则A∩B一定是( )
A. B.或{1}
C.{1} D.{}
解析:令x2=1,得x=±1;令x2=2,得x=±.由映射的定义知,集合A可能含元素1,可能不含元素1,若1∈A,则A∩B={1};若1A,则A∩B=,
∴A∩B={1}或.
答案:B
5.下列大小关系正确的是( )
A.0.43<30.4<log40.3 B.0.43<log40.3<30.4
C.log40.3<0.43<30.4 D.log40.3<30.4<0.43
解析:∵log40.3<log41=0,0<0.43<0.40=1,
30.4>30=1,∴log40. 3<0.43<30.4.
答案:C
6.已知f(x)=
则f(f(2))的值是( )
A.0 B.1
C.2 D.3
解析:∵f(2)=log3(22-1)=log33=1,
∴f(f(2))=f(1)=2e1-1=2.
答案:C
7.设x0是方程ln x+x=4的解,则x0属于区间( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
解析:令y1=ln x,y2=4-x,在同一坐标系中画出它们的图像如图所示.
由图像观察可知x0∈(2,3).
答案:C
8.李明放学回家的路上,开始和同学边走边讨论问题,走得比较慢;然后他们索性停下来将问题彻底解决;最后他快速地回到了家.下列图像中与这一过程吻合得最好的是( )
解析:根据实际情况较吻合的应为D.
答案:D
9.若一次函数f(x)=ax+b有一个零点x=2,则函数g(x)=bx2-ax的图像可能是( )
解析:由题意知2a+b=0,∴a=-,
∴g(x)=bx2+x=b(x2+x)=b(x+)2-,
令g(x)=0,得x=0或x=-0.5,故选C.
答案:C
10.若函数y=f(x)定义域为R,且满足f(-x)=-f(x),当a,b∈(-∞,0]时总有>0(a≠b),若f(m+1)>f(2),则实数m的取值范围是( )
A.-3≤m≤1 B.m>1
C.-3<m<1 D.m<-3或m>1
解析:∵当a,b∈(-∞,0]时总有>0(a≠b),∴当a,b∈(-∞,0],a-b与f(a)-f(b)同号,∴f(x)在(-∞,0]上单调递增,
又∵f(-x)=-f(x),
∴f(x)为奇函数,
∴f(x)在R上为增函数,
∴由f(m+1)>f(2)得,m+1>2,
∴m>1.
答案:B
二、填空题(本大题共4小题,每小题5分,满分20分.把答案填写在题中的横线上)
11.计算log2+log23·log3=________.
解析:原式=log ()3+·=3-1=2.
答案:2
12设f(x)是定义在R上的偶函数,且当x>0时,f(x)=2x-3,则f(-2)=________.
解析:f(-2)=f(2)=22-3=1.
答案:1
13.设函数f(x)=若f(x0)>2,则x0的取值范围是________.
解析:当x0≤0时,f(x0)=()x0>2,得x0<-1;
当x0>0时,f(x0)=x0>2,得x0>4.
∴x0的取值范围为(-∞,-1)∪(4,+∞).
答案:(-∞,-1)∪(4,+∞)
14.下列叙述:
①存在m∈R,使f(x)=(m-1)·xm2-4m+3是幂函数;
②函数y=在(-∞,-1)∪(-1,+∞)上是减函数;
③函数y=log2x+x2-2在(1,2)内只有一个零点;
④定义域内任意两个变量x1,x2,都有>0,则f(x)在定义域内是增函数.
其中正确的结论序号是________.
解析:①使f(x)=(m-1)·xm2-4m+3是幂函数,则
m-1=1,得m=2,此时f(x)=x-1,故①正确;
②减区间应为(-∞,-1)和(-1,+∞)不能合并,故②错误;
③∵f(1)=log21+1-2=-1<0,f(2)=lg 22+22-2=3>0
∴f(1) f(2)<0,且f(x)在(1,2)单调递增.故③正确;
④由已知得x1-x2与f(x1)-f(x2)同号,∴f(x)在定义域上为增函数.
综上知①③④正确.
答案:①③④
三、解答题(本大题共4小题,满分50分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分12分)已知A={x|x2+2x-8=0},B={x|log2(x2-5x+8)=1},C={x|x2-ax+a2-19=0}.
若A∩C=,B∩C≠,求a的值.
解:A={2,-4},B={2,3},
由A∩C=,知2C,-4C,
又由B∩C≠,知3∈C,
∴32-3a+a2-19=0,解得a=-2或a=5
当a=-2时,C={3,-5},满足A∩C=,
当a=5时,C={3,2},A∩C={2}≠,舍去,
∴a=-2.
16.(本小题满分12分)已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R).
(1)当函数f(x)的图像过点(-1,0),且方程f(x)=0有且只有一个根,求f(x)的表达式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(3)若F(x)=当mn<0,m+n>0,a>0,且函数f(x)为偶函数时,试判断F(m)+F(n)能否大于0
解:(1)因为f(-1)=0,所以a-b+1=0.
因为方程f(x)=0有且只有一个根,
所以Δ=b2-4a=0.
所以b2-4(b-1)=0.
即b=2,a=1.
所以f(x)=(x+1)2;
(2)因为g(x)=f(x)-kx=x2+2x+1-kx
=x2-(k-2)x+1
=(x-)2+1-.
所以当≥2或≤-2时,
即k≥6或k≤-2时,g(x)是单调函数;
(3)f(x)为偶函数,所以b=0.
所以f(x)=ax2+1.
所以F(x)=
因为mn<0,不妨设m>0,则n<0.
又因为m+n>0,所以m>-n>0.
所以|m|>|-n|.
此时F(m)+F(n)=f(m)-f(n)=am2+1-an2-1=a(m2-n2)>0.
所以F(m)+F(n)>0.
17.(本小题满分12分)如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
(1)写出y关于x的函数关系式,指出这个函数的定义域;
(2)当AE为何值时,绿地面积最大?
解:(1)S△AEH=S△CFG=x2,
S△BEF=S△DGH
=(a-x)(2-x).
∴y=S△ABCD-2S△AEH-2S△BEF
=2a-x2-(a-x)(2-x)
=-2x2+(a+2)x.
由得0<x≤2,
∴y=-2x2+(a+2)x,0<x≤2;
(2)当<2,即2<a<6时,
则x=时,y取最大值;
当≥2,即a≥6时,y=-2x2+(a+2)x,在(0,2]上是增函数,则x=2时,y取最大值2a-4
综上所述:当2<a<6时,AE=时,绿地面积取最大值;
当a≥6时 AE=2时,绿地面积取最大值2a-4.
18.(本小题满分14分)已知函数f(x)定义域为[-1,1],若对于任意的x,y∈[-1,1],都有f(x+y)=f(x)+f(y),且x>0时,有f(x)>0.
(1)证明:f(x)为奇函数;
(2)证明:f(x)在[-1,1]上是增加的;
(3)设f(1)=1,若f(x)<m-2am+2,对所有x∈[-1,1],a∈[-1,1]恒成立,求实数m的取值范围.
解:(1)令x=y=0,∴f(0)=0.
令y=-x,f(x)+f(-x)=0.
∴f(-x)=-f(x),∴f(x)为奇函数;
(2)∵f(x)是定义在[-1,1]上的奇函数,
令-1≤x1<x2≤1,
则f(x2)-f(x1)=f(x2-x1)>0
∴f(x)在[-1, 1]上是增加的;
(3)f(x)在[-1,1]上是增加的,f(x)max=f(1)=1,使f(x)<m-2am+2对所有x∈[-1,1]恒成立,只要m-2am+2>1,即m-2am+1>0.
令g(a)=m-2am+1=-2am+m+1,
要使g(a)>0时a∈[-1,1]恒成立,则
即-
