人教版八年级上册数学11.1.3三角形的稳定性 同步训练(含答案)
文档属性
| 名称 | 人教版八年级上册数学11.1.3三角形的稳定性 同步训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 154.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 09:18:52 | ||
图片预览

文档简介
人教版八年级上册数学11.1.3三角形的稳定性同步训练
一、单选题
1.下列图形中具有稳定性的是( )
A. B. C. D.
2.如图,为防止变形,木工师傅做好门框后,常常像图中所示那样钉上两根斜拉的木条(即图中的AB、CD两根木条),这样做的数学原理是( )
A.两点确定一条直线 B.两点之间,线段最短 C.美学原理 D.三角形的稳定性
3.如图所示,一扇窗户打开后,用窗钩AB即可固定,这里所用的几何原理是( )
A.两点之间线段最短 B.垂线段最短.
C.两定确定一条直线 D.三角形具有稳定性
4.下列图形中有稳定性的是( )
A.正方形 B.长方形 C.直角三角形 D.平行四边形
5.如图,电线杆的斜拉钢索是三角形的结构,主要是为了( )
A.节省材料 B.保持对称
C.利用三角形的稳定性 D.利用四边形的不稳定性
6.下列生活中的实例利用到三角形的稳定性的是( )
A.自行车的三角车架 B.用两颗钉子把木条固定在墙上
C.学校大门口的伸缩门 D.四条腿的方桌
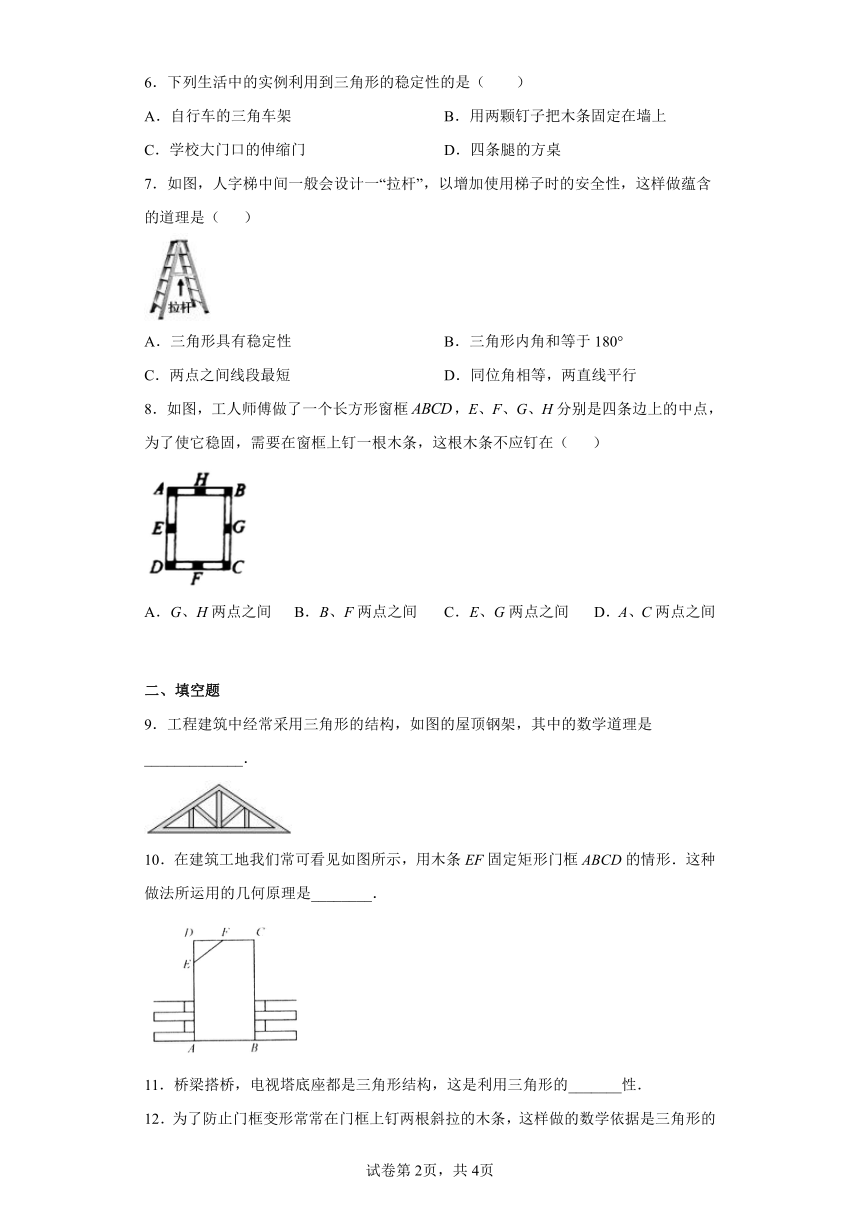
7.如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性,这样做蕴含的道理是( )
A.三角形具有稳定性 B.三角形内角和等于180°
C.两点之间线段最短 D.同位角相等,两直线平行
8.如图,工人师傅做了一个长方形窗框,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.G、H两点之间 B.B、F两点之间 C.E、G两点之间 D.A、C两点之间
二、填空题
9.工程建筑中经常采用三角形的结构,如图的屋顶钢架,其中的数学道理是 _____________.
10.在建筑工地我们常可看见如图所示,用木条EF固定矩形门框ABCD的情形.这种做法所运用的几何原理是________.
11.桥梁搭桥,电视塔底座都是三角形结构,这是利用三角形的_______性.
12.为了防止门框变形常常在门框上钉两根斜拉的木条,这样做的数学依据是三角形的____.
13.下列生产和生活实例:①用人字架来建筑房屋;②用窗钩来固定窗扇;③在栅栏门上斜钉着一根木条;④商店的推拉活动防盗门等.其中,用到三角形的稳定性的有________(填写序号).
14.工人师傅做门时,常用木条固定长方形门框,使其不变形,这种做法的根据是 __________.
15.如图,为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的_____性.
16.工程师设计屋顶时通常把钢架屋顶设计成三角形,这样做应用的数学原理是 ___________.
三、解答题
17.下列图形中哪些具有稳定性?
18.如图,ABCD是四根木条钉成的四边形,为了使它不变形,小明加了根木条AE,小明的做法正确吗?说说你的理由.
19.如图(1)扭动三角形木架, 它的形状会改变吗?
如图(2)扭动四边形木架, 它的形状会改变吗?
如图(3)斜钉一根木条的四边形木架的形状形状会改变吗?为什么?
归纳:①三角形木架的形状______,说明三角形具有______;
②四边形木架的形状______说明四边形没有______.
20.如图,是一个用六根竹条连接而成的凸六边形风筝骨架,考虑到骨架的稳固性、美观性、实用性等因素,需再加竹条与其顶点连接.要求:
(1)在图(1)、(2)中分别加适当根竹条,设计出两种不同的连接方案.
(2)通过上面的设计,可以看出至少需再加 根竹条,才能保证风筝骨架稳固、美观和实用.
(3)在上面的方案设计过程中,你所应用的数学道理是.
试卷第1页,共3页
试卷第4页,共4页
参考答案:
1.C2.D3.D4.C5.C6.A7.A8.C9.三角形具有稳定性10.三角形的稳定性11.稳定12.稳定性13.①②③14.三角形的稳定性15.稳定16.三角形具有稳定性17.(1)(4)(6)中的图形具有稳定性.18.小明的做法正确,理由见解析.19.图(1)扭动三角形木架, 它的形状不会改变,因为三角形具有稳定性;
图(2)扭动四边形木架, 它的形状会改变,四边形不稳定;
图(3)斜钉一根木条的四边形木架的形状形状不会改变,四边形变成两个三角形,三角形具有稳定性;
归纳:①是三角形, 稳定性;②四边形, 稳定性 .20.(2)三;(3)三角形的稳定性.
答案第1页,共2页
答案第1页,共1页
一、单选题
1.下列图形中具有稳定性的是( )
A. B. C. D.
2.如图,为防止变形,木工师傅做好门框后,常常像图中所示那样钉上两根斜拉的木条(即图中的AB、CD两根木条),这样做的数学原理是( )
A.两点确定一条直线 B.两点之间,线段最短 C.美学原理 D.三角形的稳定性
3.如图所示,一扇窗户打开后,用窗钩AB即可固定,这里所用的几何原理是( )
A.两点之间线段最短 B.垂线段最短.
C.两定确定一条直线 D.三角形具有稳定性
4.下列图形中有稳定性的是( )
A.正方形 B.长方形 C.直角三角形 D.平行四边形
5.如图,电线杆的斜拉钢索是三角形的结构,主要是为了( )
A.节省材料 B.保持对称
C.利用三角形的稳定性 D.利用四边形的不稳定性
6.下列生活中的实例利用到三角形的稳定性的是( )
A.自行车的三角车架 B.用两颗钉子把木条固定在墙上
C.学校大门口的伸缩门 D.四条腿的方桌
7.如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性,这样做蕴含的道理是( )
A.三角形具有稳定性 B.三角形内角和等于180°
C.两点之间线段最短 D.同位角相等,两直线平行
8.如图,工人师傅做了一个长方形窗框,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.G、H两点之间 B.B、F两点之间 C.E、G两点之间 D.A、C两点之间
二、填空题
9.工程建筑中经常采用三角形的结构,如图的屋顶钢架,其中的数学道理是 _____________.
10.在建筑工地我们常可看见如图所示,用木条EF固定矩形门框ABCD的情形.这种做法所运用的几何原理是________.
11.桥梁搭桥,电视塔底座都是三角形结构,这是利用三角形的_______性.
12.为了防止门框变形常常在门框上钉两根斜拉的木条,这样做的数学依据是三角形的____.
13.下列生产和生活实例:①用人字架来建筑房屋;②用窗钩来固定窗扇;③在栅栏门上斜钉着一根木条;④商店的推拉活动防盗门等.其中,用到三角形的稳定性的有________(填写序号).
14.工人师傅做门时,常用木条固定长方形门框,使其不变形,这种做法的根据是 __________.
15.如图,为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的_____性.
16.工程师设计屋顶时通常把钢架屋顶设计成三角形,这样做应用的数学原理是 ___________.
三、解答题
17.下列图形中哪些具有稳定性?
18.如图,ABCD是四根木条钉成的四边形,为了使它不变形,小明加了根木条AE,小明的做法正确吗?说说你的理由.
19.如图(1)扭动三角形木架, 它的形状会改变吗?
如图(2)扭动四边形木架, 它的形状会改变吗?
如图(3)斜钉一根木条的四边形木架的形状形状会改变吗?为什么?
归纳:①三角形木架的形状______,说明三角形具有______;
②四边形木架的形状______说明四边形没有______.
20.如图,是一个用六根竹条连接而成的凸六边形风筝骨架,考虑到骨架的稳固性、美观性、实用性等因素,需再加竹条与其顶点连接.要求:
(1)在图(1)、(2)中分别加适当根竹条,设计出两种不同的连接方案.
(2)通过上面的设计,可以看出至少需再加 根竹条,才能保证风筝骨架稳固、美观和实用.
(3)在上面的方案设计过程中,你所应用的数学道理是.
试卷第1页,共3页
试卷第4页,共4页
参考答案:
1.C2.D3.D4.C5.C6.A7.A8.C9.三角形具有稳定性10.三角形的稳定性11.稳定12.稳定性13.①②③14.三角形的稳定性15.稳定16.三角形具有稳定性17.(1)(4)(6)中的图形具有稳定性.18.小明的做法正确,理由见解析.19.图(1)扭动三角形木架, 它的形状不会改变,因为三角形具有稳定性;
图(2)扭动四边形木架, 它的形状会改变,四边形不稳定;
图(3)斜钉一根木条的四边形木架的形状形状不会改变,四边形变成两个三角形,三角形具有稳定性;
归纳:①是三角形, 稳定性;②四边形, 稳定性 .20.(2)三;(3)三角形的稳定性.
答案第1页,共2页
答案第1页,共1页
