勾股定理教学课件
图片预览



文档简介
课件21张PPT。勾股定理烟墩中学 王贵林 读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图1-2是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
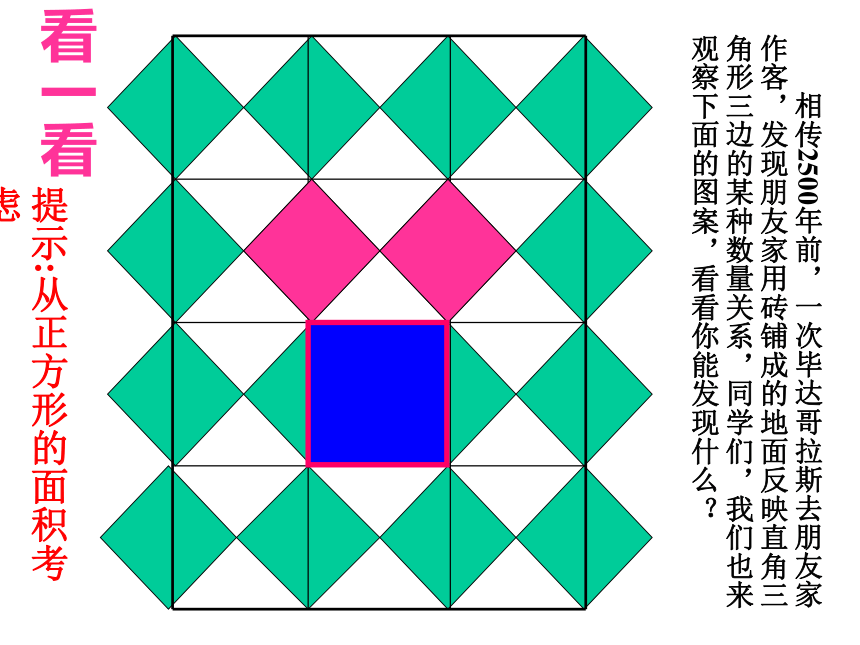
图1-2看一看 相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?提示:从正方形的面积考虑(图中每个小方格代表一个单位面积)图2-1(1)观察图2-1
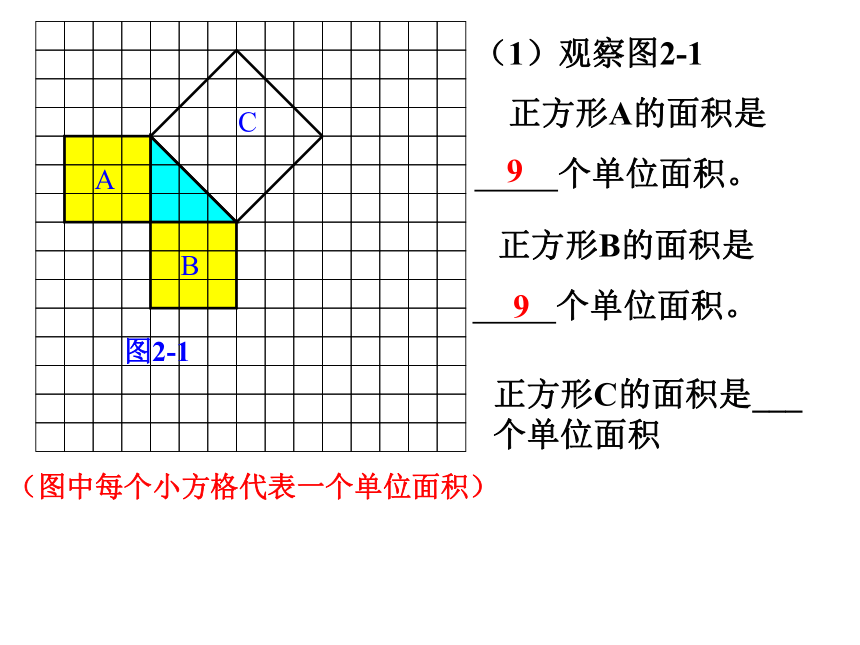
正方形A的面积是
个单位面积。 正方形B的面积是
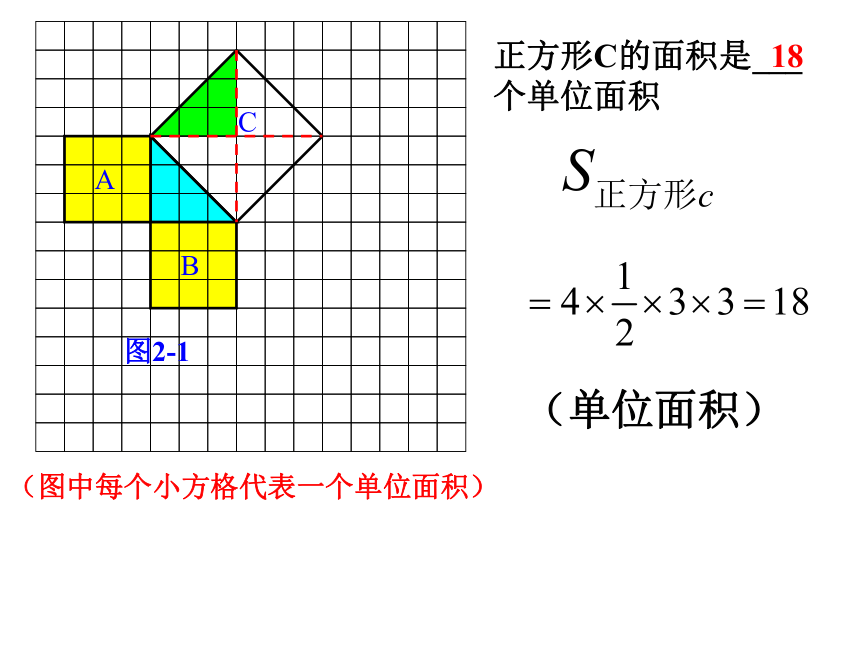
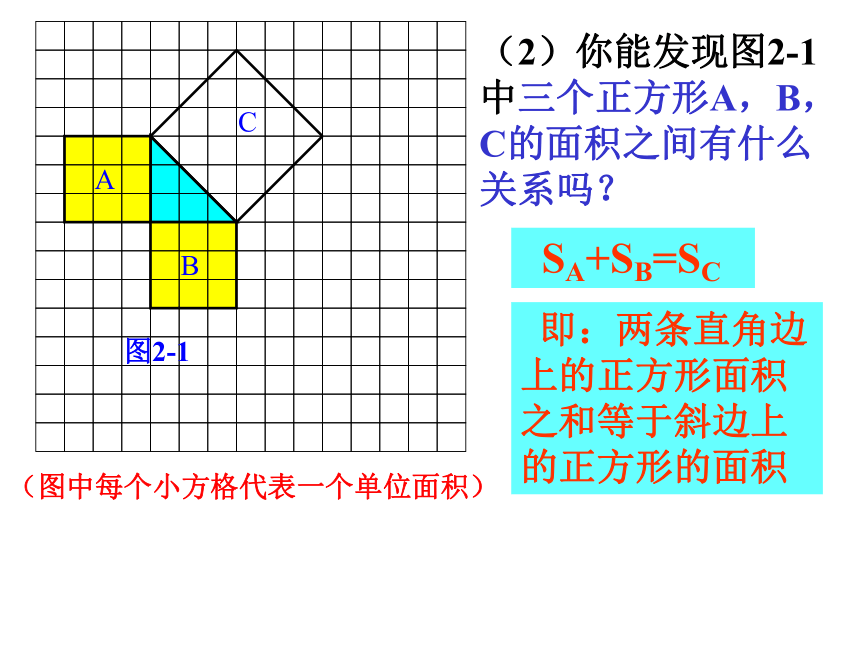
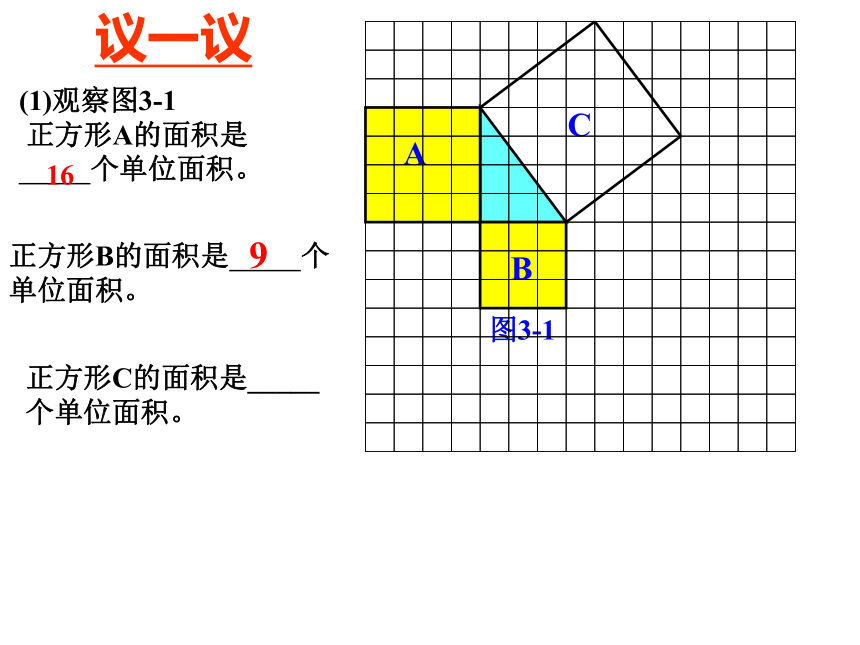
个单位面积。99正方形C的面积是___个单位面积(图中每个小方格代表一个单位面积)图2-1(单位面积)正方形C的面积是___个单位面积18(图中每个小方格代表一个单位面积)图2-1(2)你能发现图2-1中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 即:两条直角边上的正方形面积之和等于斜边上的正方形的面积ABC图3-1议一议 (1)观察图3-1
正方形A的面积是
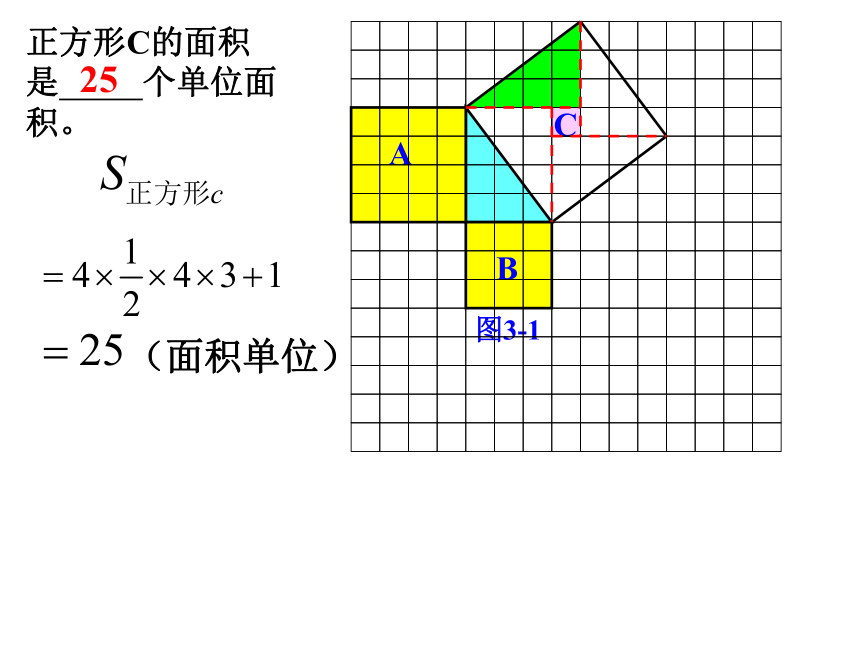
个单位面积。正方形B的面积是 个单位面积。正方形C的面积是_____ 个单位面积。169ABC图3-1(面积单位)正方形C的面积是 个单位面积。25(1)你能发现图3-1中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 即:两条直角边上的正方形面积之和等于斜边上的正方形的面积(2)设直角三角形的直角边分别为a,b,斜边为c你能用三角形的边长表示正方形的面积吗? 根据上面的讨论,你有什么发现?温馨提示:猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2ABC图3-1abca2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方.勾股弦 勾股定理温馨提示:1、只在直角三角形中适用2、记住勾股定理的文字叙述(直角边的平方和等于斜边的平方),公式形式并不总成立,它随着三角形的顶点字母不同而不同 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。 实际上我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。思考:你能验证吗?验证:c2取四个全等的直角三角形,它们的短直角边为a,长直角边为b,斜边为c如图所示a2b2? a2 + b2 = c2a2b2a2c2对比两个图形,你能直接观察验证出勾股定理吗?某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火? 解决问题:(解决本节课开头提出的问题)1、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。3、学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。小结:作业:1、请同学们回家搜集勾定理的证明方法,第二天带来与同学交流并展示
2、P69~P70 1、2美丽的勾股树
谢谢!再见!
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图1-2是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
图1-2看一看 相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?提示:从正方形的面积考虑(图中每个小方格代表一个单位面积)图2-1(1)观察图2-1
正方形A的面积是
个单位面积。 正方形B的面积是
个单位面积。99正方形C的面积是___个单位面积(图中每个小方格代表一个单位面积)图2-1(单位面积)正方形C的面积是___个单位面积18(图中每个小方格代表一个单位面积)图2-1(2)你能发现图2-1中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 即:两条直角边上的正方形面积之和等于斜边上的正方形的面积ABC图3-1议一议 (1)观察图3-1
正方形A的面积是
个单位面积。正方形B的面积是 个单位面积。正方形C的面积是_____ 个单位面积。169ABC图3-1(面积单位)正方形C的面积是 个单位面积。25(1)你能发现图3-1中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 即:两条直角边上的正方形面积之和等于斜边上的正方形的面积(2)设直角三角形的直角边分别为a,b,斜边为c你能用三角形的边长表示正方形的面积吗? 根据上面的讨论,你有什么发现?温馨提示:猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2ABC图3-1abca2+b2=c2acb 直角三角形两直角边的平方和等于斜边的平方.勾股弦 勾股定理温馨提示:1、只在直角三角形中适用2、记住勾股定理的文字叙述(直角边的平方和等于斜边的平方),公式形式并不总成立,它随着三角形的顶点字母不同而不同 两千多年前,古希腊有个哥拉 斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955勾 股 世 界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前 两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。 实际上我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。思考:你能验证吗?验证:c2取四个全等的直角三角形,它们的短直角边为a,长直角边为b,斜边为c如图所示a2b2? a2 + b2 = c2a2b2a2c2对比两个图形,你能直接观察验证出勾股定理吗?某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火? 解决问题:(解决本节课开头提出的问题)1、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。3、学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。小结:作业:1、请同学们回家搜集勾定理的证明方法,第二天带来与同学交流并展示
2、P69~P70 1、2美丽的勾股树
谢谢!再见!
