湘教版数学七年级下册第5章 轴对称与旋转 单元测试(含答案)
文档属性
| 名称 | 湘教版数学七年级下册第5章 轴对称与旋转 单元测试(含答案) | 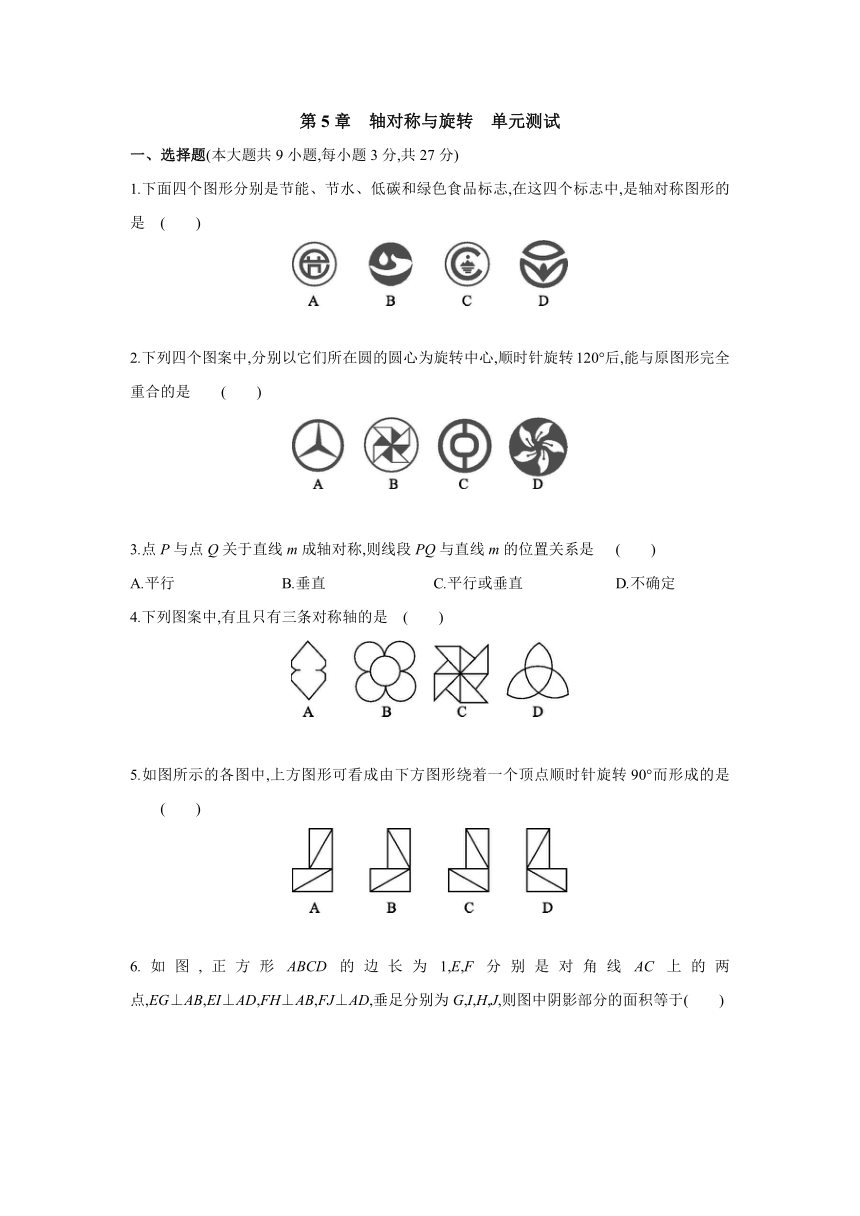 | |
| 格式 | docx | ||
| 文件大小 | 281.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 15:20:56 | ||
图片预览



文档简介
第5章 轴对称与旋转 单元测试
一、选择题(本大题共9小题,每小题3分,共27分)
1.下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是 ( )
2.下列四个图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是 ( )
3.点P与点Q关于直线m成轴对称,则线段PQ与直线m的位置关系是 ( )
A.平行 B.垂直 C.平行或垂直 D.不确定
4.下列图案中,有且只有三条对称轴的是 ( )
5.如图所示的各图中,上方图形可看成由下方图形绕着一个顶点顺时针旋转90°而形成的是 ( )
6.如图,正方形ABCD的边长为1,E,F分别是对角线AC上的两点,EG⊥AB,EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J,则图中阴影部分的面积等于( )
A.1 B. C. D.
7.已知l1∥l2,把三角形ABC(其中∠ABC=90°,∠ACB=30°)按图所示的方式摆放,边BC在直线l2上,将三角形ABC绕点C顺时针旋转50°得到三角形A'B'C,则∠1的度数为 ( )
A.20° B.50° C.80° D.110°
8.下列各组图中,由图形甲变成图形乙,既能用平移,又能用旋转得到的是 ( )
9.如图,在8×8的方格纸上有两条直线EF,MN,它们相交于点O,对三角形ABC分别作下列变换:
①以点O为旋转中心逆时针旋转180°;②先以点A为旋转中心顺时针旋转90°,再向右平移4格、向上平移4格;③先以直线MN为对称轴作轴对称图形,再向上平移4格,再以点A的对应点为旋转中心顺时针旋转90°.其
中,能使三角形ABC变换成三角形PQR的是( )
A.①② B.①③ C.②③ D.①②③
二、填空题(本大题共7小题,每小题4分,共28分)
10.在地面上的一个小水洼中观察到一辆小汽车车牌号的像为,则该小汽车的车牌号是 .
11.有下列英文字母:O,T,Q,U,R,A,N,其中 是轴对称图形.
12.一个图形无论经过平移还是旋转,有以下说法:①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有发生变化.其中说法正确的是 (填序号).
13.如图所示,图形①经过 变换得到图形②;图形①经过 变换得到图形③;图形①经过 变换得到图形④.(填“平移”“旋转”或“轴对称”)
14.将长方形ABCD沿AE折叠,得到如图所示的图形,点D落在点D'处,已知∠CED'=60°,则∠AED'的度数为 .
15.如图,AD所在直线是三角形ABC的对称轴,AC=8 cm,DC=4 cm,则三角形ABC的周长为 .
图 图
16.如图所示,把三角形ABC绕点C顺时针旋转35°,得到三角形A1B1C,A1B1交AC于点D.若∠A1DC=90°,则∠A= °.
三、解答题(本大题共4小题,共45分)
17.(8分)如图,已知三角形ABC和直线m.求作:三角形DEF,使三角形DEF与三角形ABC关于直线m对称.
18.(12分)如图,在边长为1个单位的小正方形组成的10×10的网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
(1)试在图中标出点D,并画出该四边形的另外两条边;
(2)将四边形ABCD向下平移5个单位,画出平移后得到的四边形A'B'C'D'.
19.(12分)如图,将三角形ABC绕顶点A顺时针旋转得到三角形AB'C',∠B=30°,
∠C=40°.
(1)当三角形ABC顺时针旋转至少多少度时,旋转后的三角形AB'C'的顶点B'与原三角形的顶点C和顶点A在同一直线上(如图②)
(2)在(1)的基础上,再继续旋转至少多少度时,点C,A,C'在同一直线上(如图③)
20.(13分)如图,四边形ABCD是正方形,三角形ADF旋转一定角度后得到三角形ABE,AF=4,AD=7.
(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何
答案
1. D
2. A
3. B
4. D
5. B 从对角线的位置及旋转方向是顺时针可知B项符合条件.
6. B
7. C 因为三角形ABC绕点C顺时针旋转50°得到三角形A'B'C,所以∠ACA'=50°,所以∠A'CB=80°.因为l1∥l2,所以∠1=∠A'CB=80°.
8. C
9. C
10. FT2567
11. O,T,U,A
12. ②③④
平移后对应线段平行;对应线段相等;对应角相等;图形的形状和大小都没有发生变化.旋转后对应线段不一定平行;对应线段相等;对应角相等;图形的形状和大小都没有发生变化.
13. 轴对称 旋转 平移
14. 60°
15. 24 cm
16. 55
17.解:三角形DEF如图所示.
18.解:(1)(2)如图所示.
19.解:(1)因为∠B=30°,∠BCA=40°,
所以∠BAC=180°-∠B-∠BCA=110°.
因为将三角形ABC绕顶点A顺时针旋转,旋转后的三角形AB'C'的顶点B'与原三角形的顶点C和顶点A在同一直线上,
所以∠BAB'=110°,所以需要旋转至少110°.
(2)若在(1)的基础上,再继续旋转,使点C,A,C'在同一直线上,则旋转后∠BAB'=180°,
所以∠CAB'=180°-110°=70°.
即在(1)的基础上,再继续旋转至少70°时,点C,A,C'在同一直线上.
20.解:(1)旋转中心是点A.按顺时针方向,旋转角度是90°;按逆时针方向,旋转角度是270°.
(2)DE=AD-AE=AD-AF=7-4=3.
(3)BE⊥DF.
一、选择题(本大题共9小题,每小题3分,共27分)
1.下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是 ( )
2.下列四个图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是 ( )
3.点P与点Q关于直线m成轴对称,则线段PQ与直线m的位置关系是 ( )
A.平行 B.垂直 C.平行或垂直 D.不确定
4.下列图案中,有且只有三条对称轴的是 ( )
5.如图所示的各图中,上方图形可看成由下方图形绕着一个顶点顺时针旋转90°而形成的是 ( )
6.如图,正方形ABCD的边长为1,E,F分别是对角线AC上的两点,EG⊥AB,EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J,则图中阴影部分的面积等于( )
A.1 B. C. D.
7.已知l1∥l2,把三角形ABC(其中∠ABC=90°,∠ACB=30°)按图所示的方式摆放,边BC在直线l2上,将三角形ABC绕点C顺时针旋转50°得到三角形A'B'C,则∠1的度数为 ( )
A.20° B.50° C.80° D.110°
8.下列各组图中,由图形甲变成图形乙,既能用平移,又能用旋转得到的是 ( )
9.如图,在8×8的方格纸上有两条直线EF,MN,它们相交于点O,对三角形ABC分别作下列变换:
①以点O为旋转中心逆时针旋转180°;②先以点A为旋转中心顺时针旋转90°,再向右平移4格、向上平移4格;③先以直线MN为对称轴作轴对称图形,再向上平移4格,再以点A的对应点为旋转中心顺时针旋转90°.其
中,能使三角形ABC变换成三角形PQR的是( )
A.①② B.①③ C.②③ D.①②③
二、填空题(本大题共7小题,每小题4分,共28分)
10.在地面上的一个小水洼中观察到一辆小汽车车牌号的像为,则该小汽车的车牌号是 .
11.有下列英文字母:O,T,Q,U,R,A,N,其中 是轴对称图形.
12.一个图形无论经过平移还是旋转,有以下说法:①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有发生变化.其中说法正确的是 (填序号).
13.如图所示,图形①经过 变换得到图形②;图形①经过 变换得到图形③;图形①经过 变换得到图形④.(填“平移”“旋转”或“轴对称”)
14.将长方形ABCD沿AE折叠,得到如图所示的图形,点D落在点D'处,已知∠CED'=60°,则∠AED'的度数为 .
15.如图,AD所在直线是三角形ABC的对称轴,AC=8 cm,DC=4 cm,则三角形ABC的周长为 .
图 图
16.如图所示,把三角形ABC绕点C顺时针旋转35°,得到三角形A1B1C,A1B1交AC于点D.若∠A1DC=90°,则∠A= °.
三、解答题(本大题共4小题,共45分)
17.(8分)如图,已知三角形ABC和直线m.求作:三角形DEF,使三角形DEF与三角形ABC关于直线m对称.
18.(12分)如图,在边长为1个单位的小正方形组成的10×10的网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
(1)试在图中标出点D,并画出该四边形的另外两条边;
(2)将四边形ABCD向下平移5个单位,画出平移后得到的四边形A'B'C'D'.
19.(12分)如图,将三角形ABC绕顶点A顺时针旋转得到三角形AB'C',∠B=30°,
∠C=40°.
(1)当三角形ABC顺时针旋转至少多少度时,旋转后的三角形AB'C'的顶点B'与原三角形的顶点C和顶点A在同一直线上(如图②)
(2)在(1)的基础上,再继续旋转至少多少度时,点C,A,C'在同一直线上(如图③)
20.(13分)如图,四边形ABCD是正方形,三角形ADF旋转一定角度后得到三角形ABE,AF=4,AD=7.
(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何
答案
1. D
2. A
3. B
4. D
5. B 从对角线的位置及旋转方向是顺时针可知B项符合条件.
6. B
7. C 因为三角形ABC绕点C顺时针旋转50°得到三角形A'B'C,所以∠ACA'=50°,所以∠A'CB=80°.因为l1∥l2,所以∠1=∠A'CB=80°.
8. C
9. C
10. FT2567
11. O,T,U,A
12. ②③④
平移后对应线段平行;对应线段相等;对应角相等;图形的形状和大小都没有发生变化.旋转后对应线段不一定平行;对应线段相等;对应角相等;图形的形状和大小都没有发生变化.
13. 轴对称 旋转 平移
14. 60°
15. 24 cm
16. 55
17.解:三角形DEF如图所示.
18.解:(1)(2)如图所示.
19.解:(1)因为∠B=30°,∠BCA=40°,
所以∠BAC=180°-∠B-∠BCA=110°.
因为将三角形ABC绕顶点A顺时针旋转,旋转后的三角形AB'C'的顶点B'与原三角形的顶点C和顶点A在同一直线上,
所以∠BAB'=110°,所以需要旋转至少110°.
(2)若在(1)的基础上,再继续旋转,使点C,A,C'在同一直线上,则旋转后∠BAB'=180°,
所以∠CAB'=180°-110°=70°.
即在(1)的基础上,再继续旋转至少70°时,点C,A,C'在同一直线上.
20.解:(1)旋转中心是点A.按顺时针方向,旋转角度是90°;按逆时针方向,旋转角度是270°.
(2)DE=AD-AE=AD-AF=7-4=3.
(3)BE⊥DF.
