狐、弦、圆心角

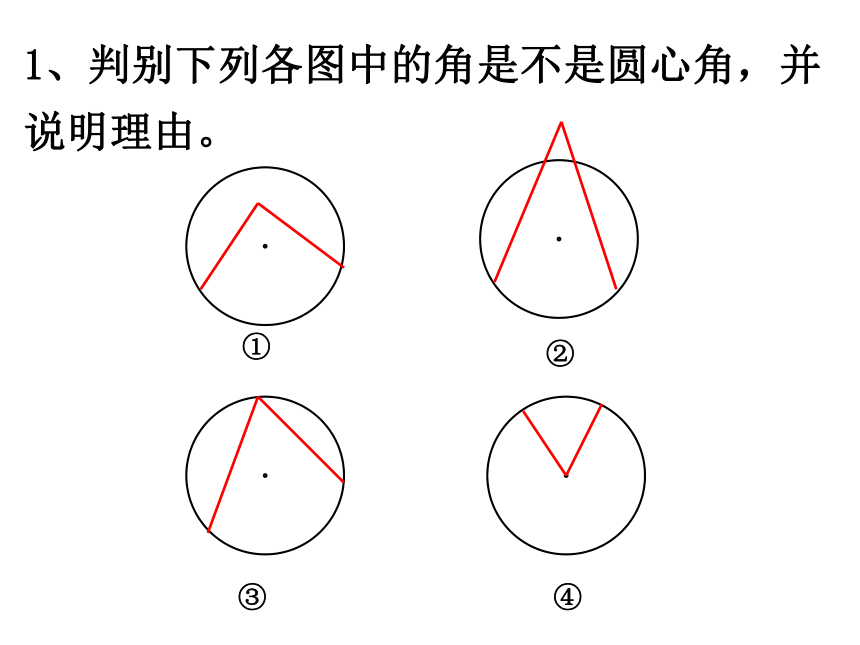
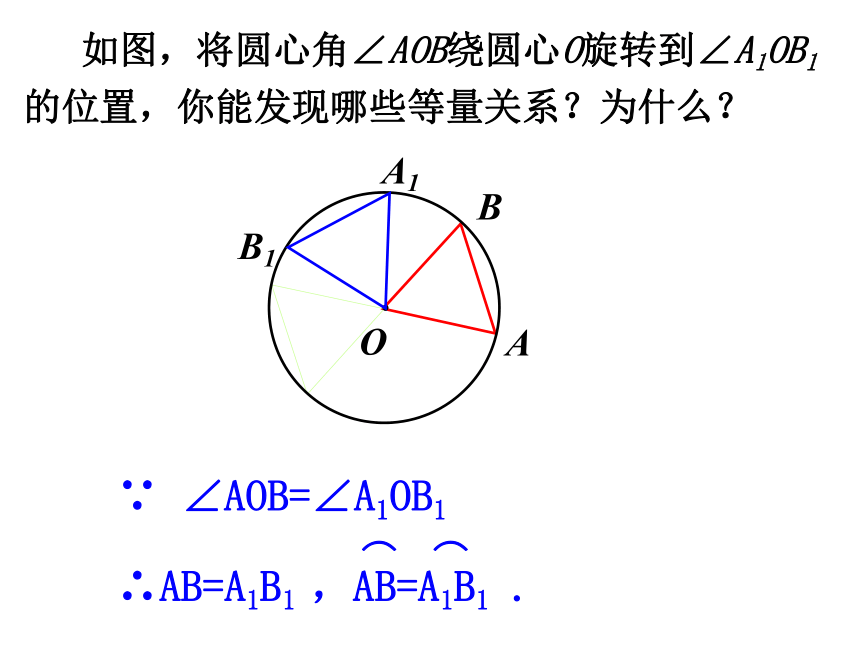
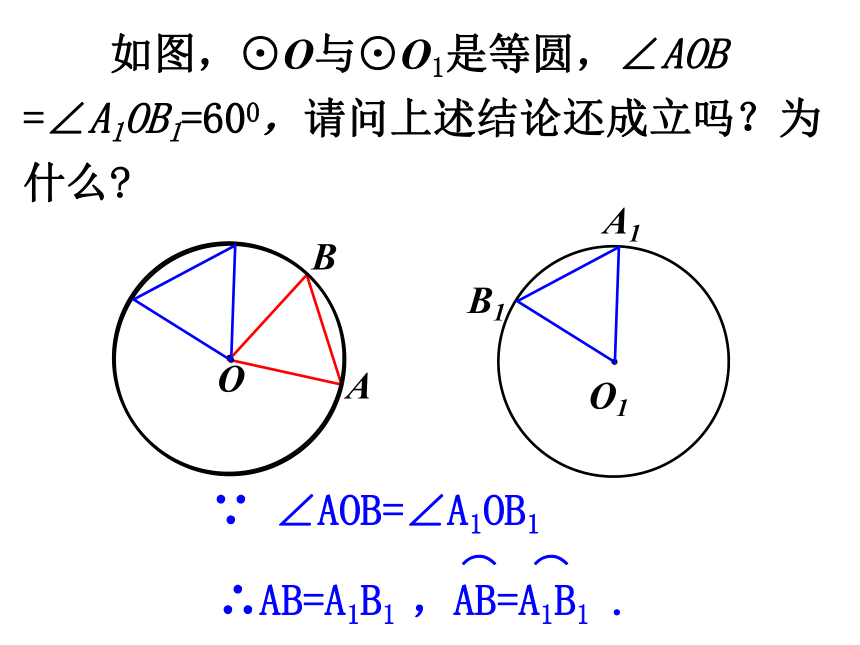
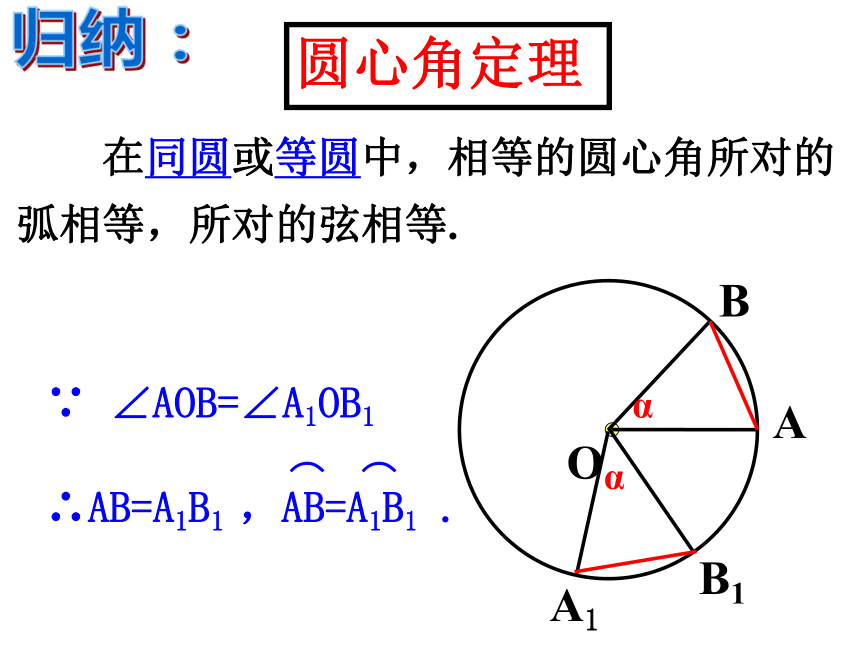
课件27张PPT。人教版九年级上册圆是中心对称图形吗?它的对称中心在哪里?·圆是中心对称图形，它的对称中心是圆心.思考：· 圆心角：我们把顶点在圆心的角叫做圆心角.O∠AOB为圆心角概念：1、判别下列各图中的角是不是圆心角，并说明理由。①②③④任意给圆心角，对应出现三个量：圆心角弧弦探究：疑问：这三个量之间会有什么关系呢？ 如图，将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置，你能发现哪些等量关系？为什么？·OABA1B1∵ ∠AOB=∠A1OB1 如图，⊙O与⊙O1是等圆，∠AOB =∠A1OB1=600，请问上述结论还成立吗？为什么?∵ ∠AOB=∠A1OB1 在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等.归纳：∵ ∠AOB=∠A1OB1圆心角定理思考：在同圆或等圆中，如果两条弧相等，你能得什么结论？在同圆或等圆中，如果两条弦相等呢？
αABA1B1α 同圆或等圆中，两个圆心角、两条圆心角所对的弧、两条圆心角所对的弦中如果有一组量相等，它们所对应的其余各组量也相等。等对等定理延伸：(1) 圆心角(2) 弧(3) 弦知一得二等对等定理整体理解：αABA1B1α1、如图3，AB、CD是⊙O的两条弦。
（1）如果AB=CD，那么 ， 。
（2）如果弧AB=弧CD，那么 ， 。
（3）如果∠AOB=∠COD，那么 ， 。
（4）如果AB=CD，OE⊥AB于E，
OF⊥CD于F，OE与OF相等吗？
为什么？巩固：证明： ∵AB=AC
∴AB=AC，△ABC是等腰三角形　　
又 ∠ACB=60°
∴△ABC是等边三角形，AB=BC=CA
∴∠AOB=∠BOC=∠AOC例1 如图1，在⊙O中，AB=AC,∠ACB=60°,　　　　
求证∠AOB=∠BOC=∠AOC。例题：⌒⌒⌒⌒2、如图4，AB是⊙O的直径，BC=CD=DE，∠COD=35°，求∠AOE的度数。证明： ∵ BC=CD=DE
∴∠COB=∠COD=∠DOE=35°
∴∠AOE=1800-∠COB-∠COD-∠DOE
=750⌒⌒⌒⌒⌒⌒3、如图6，AD=BC，那么比较AB与CD的大小.⌒⌒4、如图7所示，CD为⊙O的弦，在CD上取
CE=DF，连结OE、OF，并延长交⊙O于点A、
B.
（1）试判断△OEF的形状，并说明理由；
（2）求证：AC=BD⌒⌒5、如图，等边△ABC的三个顶点A、B、C都在⊙O上，连接OA、OB、OC，延长AO分别交BC于点P，交BC于点D，连接BD、CD.
（1）判断四边形BDCO的形状，并说明理由；
（2）若⊙O的半径为r，求△ABC的边长⌒1、三个元素：
圆心角、弦、弧归纳：2、三个相等关系：(1) 圆心角相等(2) 弧相等(3) 弦相等知一得二综合练习类型之二 利用“弧、弦、圆心角之间的关系”进行证明3.如图，AB、AC、BC都是⊙O的弦，且∠CAB=∠CBA，
求证：∠COB=∠COA4.变式题：已知⊙0中的弦AB=CD。
求证：（1） ； （2）∠AOC=∠BOD。第3题第4题类型之三 弧、弦、圆心角之间的关系的综合运用5.如图，A、B、C为⊙0上的三点，且有 ，连结AB、BC、CA。
（1）试确定△ABC的形状（2）若AB=a，求⊙0的半径。6．如图，AC与BD为⊙O的弦，且 AC=BD，
求证： 5.如图，A、B、C为⊙0上的三点，且有 ，连结AB、BC、CA。
（1）试确定△ABC的形状（2）若AB=a，求⊙0的半径。7．在⊙O中， ，则下列结论正确的（ ）
A．AB=2CD B．AB>2CD C．AB<2CD
D．无法确定8.如图，AB为⊙O的直径，C、D分别为OA、OB的中点，CF⊥AB,DE⊥AB.下列结论：
①CF=DE;② ;③AE=2CF;④四边形CDFE为正方形.其中正确的是（ ）
A. ①②③ B. ①② C. ②③④ D. ①③④9．如图，P为⊙O外一点，PB，PD分别交⊙O于A，B，C，D，PO平分∠BPD，
求证：∠AOB=∠COD（提示：可以过点O分别作∠BPD的两边的距离）拓展与延伸（选学、选做） 10．如图，已知：点O是∠EPF的平分线上的一点，以点O为圆心的圆与角的两边分别交于点A、B和C、D。
（1）求证：AB=CD；
（2）若角的顶点P在圆上或在圆内，上述结论还成立吗？若不成立，请说明理由；若成立，请加以证明。11．如图，已知∠AOB=90°，C、D是的三等分点，AB分别交OC，OD于点E，F.下列结论：①∠AOC=30°;②CE=DF;③∠AEO=105°; ④ .其中正确的有（ ）
A.1个 B.2个 C.3个 D. 4个12.如图，点A是半圆上一个三等分点，点B是 的中点，P是直径MN上的一动点⊙O的半径为1，则PA+PB的最小值为_______.