轴对称现象

课件24张PPT。§7.1 轴对称现象
破茧成蝶面对生活中这些美丽的图片，
你是否强烈地感受到美就在我们身边！
这是一种怎样的美呢?
请你谈谈你的感想？实验一：探索新知 请你想一想：将上图中的每一个图形沿某条直线对折，直线两旁的部分能完全重合吗？我们能不能给具有这样特征的一个图形起一个名称呢？轴对称图形 如果一个图形沿某条直线对折后，直线两旁的部分能够完全重合，那么这个图形叫做轴对称图形。那我们就能得到第一个结论：这条直线叫这个图形的对称轴。试一试你能找出下面五角星的对称轴吗？先想一想，再动手折一折，然后画一画。
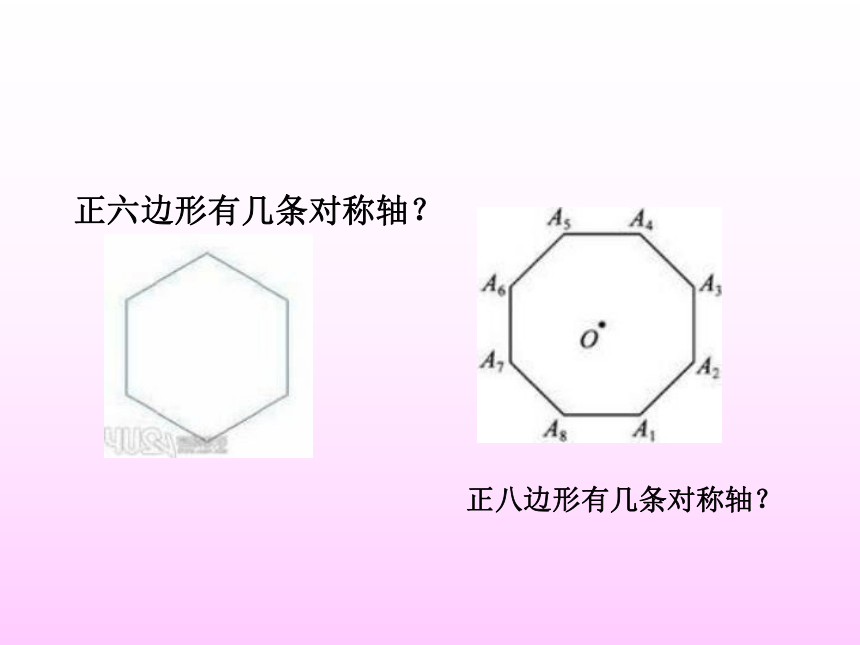
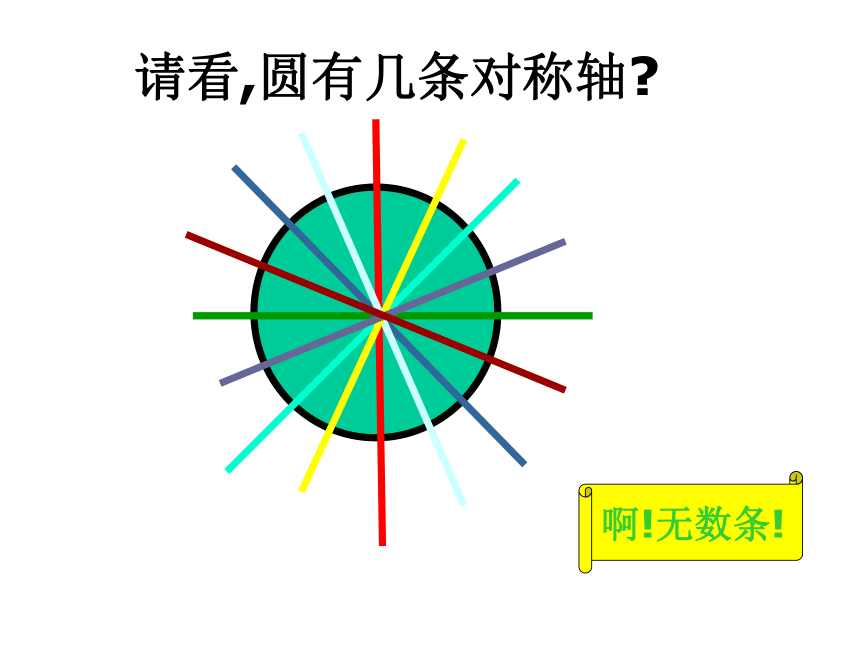
正八边形有几条对称轴？正六边形有几条对称轴？请看,圆有几条对称轴?啊!无数条!下列图形哪些是轴对称图形?退出√××√√√√√√×××练一练A、1个　　B、2个　　C、3个　　D、4个A、1个　　B、2个　　C、3个　　D、4个。BC请大家再看看左面两组图形
每一组里，左边的图形沿直线对折后与右边的图形完全重合吗？
对于两个图形，如果沿一条直线对折后，它们完全重合，那么就说这两个图形关于这条直线成轴对称。那我们就能得到第二个结论：这条直线就是对称轴。 轴对称图形和两个图形成轴对称的区别与联系 轴对称图形轴对称 区别联系图形 (1)轴对称图形是指( )
具有特殊形状的图形,
只对( ) 图形而言;
(2)对称轴( ) 只有一条(1)轴对称是指( )图形
的位置关系,必须涉及
( )图形;
(2)只有( )对称轴.如果把轴对称图形沿对称轴
分成两部分,那么这两个图形
就关于这条直线成轴对称.如果把两个成轴对称的图形
拼在一起看成一个整体,那
么它就是一个轴对称图形.一个一个不一定两个两个一条共同点　沿一条直线对折，对折的两部分能够完全重合两个图形成　　追问1　你能说明其中
的道理吗？ 探索新知　　问题3　如图，△ABC 和△A′B′C′关于直线MN
对称，点A′,B′,C′分别是点A，B，C 的对称点，线
段AA′，BB′，CC′与直线MN 有什么关系？探索新知　　追问2　上面的问题说明“如果△ABC 和
△A′B′C′关于直线MN 对称，那么，直线MN 垂直
线段AA′，BB′和CC′，并且直线MN 还平分线段
AA′，BB′和CC′”．如
果将其中的“三角形”改为
“四边形”“五边形”…其
他条件不变，上述结论还成
立吗？ 　　经过线段中点并且垂直
于这条线段的直线，叫做这
条线段的垂直平分线． 探索新知　　问题3　如图，△ABC 和△A′B′C′关于直线MN
对称，点A′,B′,C′分别是点A，B，C 的对称点，线
段AA′，BB′，CC′与直线MN 有什么关系？探索新知　　追问3　你能用数学语言概括前面的结论吗？ 　　成轴对称的两个图形的性质：
　　如果两个图形关于某条
直线对称，那么对称轴是任
何一对对应点所连线段的垂
直平分线．即对称点所连线
段被对称轴垂直平分；对称
轴垂直平分对称点所连线段． 　　结论：
　　直线l 垂直线段AA′，BB′，
直线l平分线段AA′，BB′（或直
线l 是线段AA′，BB′的垂直平分
线）． 探索新知　　问题4　下图是一个轴对称图形，你能发现什么结
论？能说明理由吗？ 　　追问　你能用数学语言概括前面
的结论吗？ 探索新知　　问题4　下图是一个轴对称图形，你能发现什么结
论？能说明理由吗？ 　　轴对称图形的性质：
轴对称图形的对称轴，是任何
一对对应点所连线段的垂直平分线． 探索新知　　问题4　下图是一个轴对称图形，你能发现什么结
论？能说明理由吗？ 在图形中标出点和关于直线的对称点ACBDD挑战自我！ 1、下列平面图形中，不是轴对称图形的是： （ ）2、DB