2.6.1 应用一元二次方程 课件(共28张PPT)
文档属性
| 名称 | 2.6.1 应用一元二次方程 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 693.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 20:55:21 | ||
图片预览







文档简介
(共28张PPT)
北师大版九年级上册
第二章
一元二次方程
2.6 应用一元二次方程(一)
列方程解应用题的一般步骤是:
1.审:审清题意,找等量关系
2.设:设未知数,语句要完整,有单位的要注明单位;
3.列:列代数式,列方程;
4.解:解所列的方程;
5.验:是否是所列方程的解;是否符合题意;
6.答:答案也必需是完整的语句,注明单位.
列方程解应用题的关键是: 找出相等关系
一、复习回顾
本章开始时梯子下滑的问题:.
如图,一个长为10m的梯子斜靠在墙上,梯子顶端距地面的垂直距离为8m.
(1)如果梯子的顶端下滑1m,那梯子的底端滑动多少米?
一、复习回顾
解:由勾股定理知,滑动前梯子底端距墙6 m
设梯子底端滑动x m,那么滑动后梯子底端距墙(6+x)m
72+(x+6)2=102
本章开始时梯子下滑的问题:.
如图,一个长为10m的梯子斜靠在墙上,梯子顶端距地面的垂直距离为8m.
(2)梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
一、复习回顾
(8-x)2+(x+6)2=102
设梯子顶端下滑x m,梯子底端滑动(6+x)m,得
解:由勾股定理知,滑动前梯子底端距墙6 m
本章开始时梯子下滑的问题:.
(3)如果梯子的长度是 13 m,梯子顶端与地面的垂直距离为 12 m,那么梯子顶端下滑的距离与梯子的底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
一、复习回顾
(12-x)2+(x+5)2=132
设梯子顶端下滑x m,那么滑动后梯子底端距墙(5+x)m
解:由勾股定理知,滑动前梯子底端距墙5 m
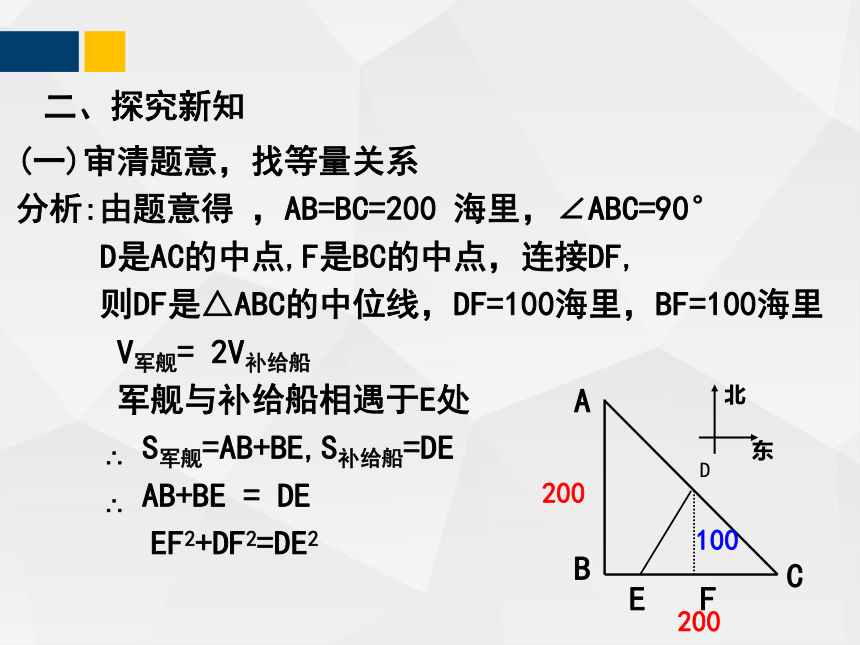
如图,某海军基地位于点A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰从A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
A
B
D
C
E
F
北
东
已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里 (结果精确到0.1海里)
二、探究新知
(一)审清题意,找等量关系
分析:由题意得 ,AB=BC=200 海里,∠ABC=90°
D是AC的中点,F是BC的中点,连接DF,
则DF是△ABC的中位线,DF=100海里,BF=100海里
V军舰= 2V补给船
军舰与补给船相遇于E处
∴ S军舰=AB+BE,S补给船=DE
∴ AB+BE = DE
EF2+DF2=DE2
北
东
A
B
C
D
E
F
100
二、探究新知
200
200
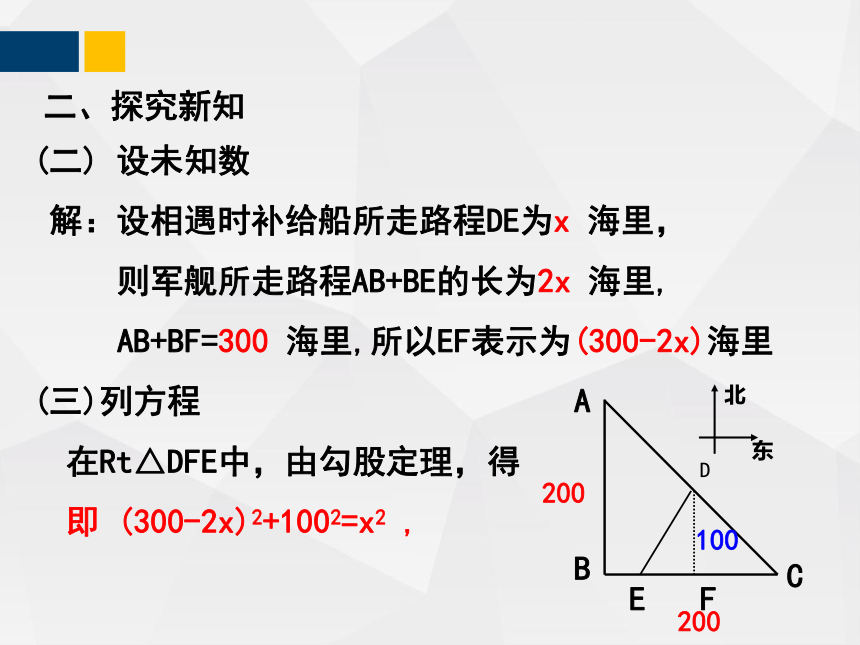
(二) 设未知数
解:设相遇时补给船所走路程DE为x 海里,
则军舰所走路程AB+BE的长为2x 海里,
AB+BF=300 海里,所以EF表示为(300-2x)海里
(三)列方程
在Rt△DFE中,由勾股定理,得
即 (300-2x)2+1002=x2 ,
北
东
A
B
C
D
E
F
100
二、探究新知
200
200
若设相遇时补给船的行程DE为x海里
连接DF.
∵AD=CD,BF=CF
∴DF是 ABC的中位线
∴DF∥AB,且DF= AB
∵AB⊥BC,AB=BC=200海里
∵DF⊥BC,DF=100海里,BF=100海里
∴EF=AB+BF-(AB+BE)=(300- 2x)海里 。
在Rt DEF中,根据勾股定理可得方程:
整理,得:
(舍去)
所以,相遇是补给船大约航行了118.4海里
解法一:
那么 DE= 海里,AB+BE= 海里
x
2x
北
东
A
B
C
D
E
F
北
东
解:连接DF.
∵AD=CD,BF=CF,
∴DF是△ABC的中位线.
∴DF∥AB,且DF= AB.
∵AB⊥BC,AB=BC=200 海里,
∴DF⊥BC,DF=100 海里, BF=100 海里.
设相遇时补给船航行了x 海里,那么
DE=x 海里, AB+BE=2x 海里,
EF=AB+BF-(AB+BE)=(300-2x) 海里.
解法二:
北
东
在Rt△DEF中,
根据勾股定理可得方程
整理,得
解这个方程,得
所以,相遇时补给船大约航行了118.4 海里.
与直角三角形有关的问题:直角三角形两直角边的平方和等于斜边的平方是这类问题的等量关系,即用勾股定理列方程.
归纳总结
《九章算术》“勾股”章中:“今有二人同所立.甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙各行几何 ”
大意是说:已知甲,乙二人同时从同一地点出发,甲的速度是7,乙
的速度是3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲,乙各走了多远
解:设甲,乙相遇时所用时间为x,根据题意,得
(7x - 10)2 = (3x) 2 +10 2.
整理得 2x2 - 7x = 0.
解方程,得 x1=3.5, x2=0 (不合题意,舍去).
∴3x=3×3.5 =10.5 , 7x = 7×3.5 = 24.5.
答:甲走了24.5步,乙走了10.5步.
O
东
北
A
B
10
3x
7x -10
如图,A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动.
(1)P,Q两点从出发开始到几秒?
四边形PBCQ的面积为33cm2;
(2)P,Q两点从出发开始到几秒时?
点P和点Q的距离是10cm.
例2:利用一元二次方程解决行程(动点)问题
解:(1)设P,Q两点运动x秒时四边形PBCQ的面积为33cm2,
则PB=(16-3x)cm,QC=2x cm.根据梯形的面积
公式得 (16-3x+2x)×6=33,解得x=5.
(2)设P,Q两点从出发经过t秒时,
点P,Q间的距离是10cm,
如图,作QE⊥AB,垂足为E,
则QE=AD=6,PQ=10.∵PA=3t,CQ=BE=2t,
∴PE=AB-AP-BE= |16-5t| .
由勾股定理,得(16-5t)2+62=102,
解得t1=4.8,t2=1.6.
答:(1)P,Q两点从出发开始到5秒时四边形PBCQ的面积为33 cm2;
(2)从出发到1.6秒或4.8秒时,点P和点Q的距离是10 cm.
1.如图,在△ABC中,∠C=90°,AB=10 cm,AC=8 cm,点P,Q同时由A,C两点出发,分别沿AC,CB方向向点C,B移动,它们的速度都是2 cm/s,经过几秒,P,Q两点相距2 cm
巩固练习
解:设经过t s,P,Q两点相距2 cm.
∴CQ=AP=t,CP=8-2t
∵∠C=90°,∴CQ2+PC2=PQ2.
∴(2t)2+(8-2t)2=(2 )2.
∴4t2+64-32t+4t2=40.
化简,得t2-4t+3=0.
解得t1=1,t2=3.经检验,t1,t2均符合题意.
答:经过1 s或3 s,P,Q两点相距2 cm
1)关键—— 动中取静
把动的点进行转换,变为线段的长度,
2)方法—— 时间变路程
求“动点的运动时间”可以转化为求“动点的运动路程”,也是求线段的长度;
由此,学会把动点的问题转化为静点的问题,
是解这类问题的关键.
3)常找的数量关系——
面积,勾股定理,相似三角形等;
归纳总结
1.如图,AB⊥BC,AB=10 cm,BC=8 cm,一只蝉从C点沿CB方向以每秒1 cm的速度爬行,蝉开始爬行的同时,一只螳螂由A点沿AB方向以每秒2 cm的速度爬行,当螳螂和蝉爬行x秒后,它们分别到达了M,N的位置,此时,△MNB的面积恰好为24 cm2,由题意可列方程( )
A.2x·x=24
B.(10-2x)(8-x)=24
C.(10-x)(8-2x)=24
D.(10-2x)(8-x)=48
D
四、课堂检测
2. 公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花,原空地一边减少了1 m,另一边减少了2 m,剩余空地的面积为18 m2,求原正方形空地的边长. 设原正方形的空地的边长为x m,则可列方程为( )
A. (x+1)(x+2)=18 B. x2-3x+16=0
C. ( x-1)(x-2)=18 D. x2+3x+16=0
C
四、课堂检测
3. 如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm. 动点P,Q分别从点A,B同时开始移动,点P的速度为1cm/s,点Q的速度为2cm/s,点Q移动到点C后停止,点P也随之停止运动. 下列时间瞬间中,能使△PBQ的面积为15cm2的是( )
A. 第2秒钟 B. 第3秒钟
C. 第4秒钟 D. 第5秒钟
四、课堂检测
B
四、课堂检测
4.如图,某农场有一块长40 m,宽32 m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1 140m2,求小路的宽.
解:设小路的宽为x m,依题意,得
(40-x)(32-x)=1 140.
整理,得x2-72x+140=0.
解得x1=2,x2=70 (不合题意,舍去)
答:小路的宽是2 m.
5.如图,在矩形ABCD中,AB=6cm, BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,那么几秒后五边形APQCD的面积为64cm2?
A
B
C
D
Q
P
解:设所需时间为 t s,根据题意,得
2t (6 - t) ÷2 = 6×12 - 64.
整理得 t2 - 6t + 8 = 0.
解方程,得 t1 = 2 , t2 = 4 .
答:在第2秒和第4秒是五边形面积是 64cm2.
(6 - t)
2t
四、课堂检测
6.某农场要建一个长方形的养鸡场,养鸡场的一边靠墙(墙长为20米),另三边用总长40米的木栏围成.要使得围成的养鸡场的面积为198米2,三边木栏的长应分别为多少米?
解:设养鸡场的宽x米,则长为(40-2x)米,得:
(40-2x) x=198
解得:x1=9,x2=11
当x=9时,长=40-2x=40-18=22>20,不符合题意,舍去;
当x=11时,长=40-2x=40-22=18<20,符合题意;
答:养鸡场的长为18米,宽为11米.
四、课堂检测
7.如图,在Rt△ABC中,∠C=90°,AC=6m,BC=8m,
(1)点P、Q同时由A、B两点出发,分别沿AC、BC的方向向点C匀速运动(到点C为止),它们的速度都是1m/s.经过几秒△PCQ的面积等于Rt△ABC面积的一半?
四、课堂检测
解:设经过x秒△PCQ的面积等于Rt△ABC面积的一半
∴AP=BQ=x m,PC=(6-x) m,CQ=(8-x) cm
(6-x)(8-x)= × ×6×8
化简得:x2-14x+24=0
解得x1=2, x1=12(不符合题意,舍去)
答:经过2秒△PCQ的面积等于Rt△ABC面积的一半.
7.如图,在Rt△ABC中,∠C=90°,AC=6m,BC=8m,
(2)点P由A出发,沿AC方向匀速运动,当点P到达点C则停止运动,点Q同时由C出发,沿CB方向匀速运动,它们的速度都是1m/s .几秒后△PCQ的面积等于△ABC面积的 ?
四、课堂检测
解:设经过x秒△PCQ的面积等于Rt△ABC面积的∴AP=CQ=x m,PC=(6-x) m
x(6-x) = × ×6×8
化简得:x2-6x+8=0
解得x1=2, x1=4
答:经过2秒或4秒△PCQ的面积等于Rt△ABC面积的.
在列一元二次方程解应用题时,由于所得的根一般有两个,所以要检验这两个根是否符合实际问题的要求.
列一元二次方程解应用题的步骤:
审、设、列、解、检、答.
五、课堂小结
六、布置作业
课本P53 习题2.9 第1,2,3,4题
谢谢聆听
北师大版九年级上册
第二章
一元二次方程
2.6 应用一元二次方程(一)
列方程解应用题的一般步骤是:
1.审:审清题意,找等量关系
2.设:设未知数,语句要完整,有单位的要注明单位;
3.列:列代数式,列方程;
4.解:解所列的方程;
5.验:是否是所列方程的解;是否符合题意;
6.答:答案也必需是完整的语句,注明单位.
列方程解应用题的关键是: 找出相等关系
一、复习回顾
本章开始时梯子下滑的问题:.
如图,一个长为10m的梯子斜靠在墙上,梯子顶端距地面的垂直距离为8m.
(1)如果梯子的顶端下滑1m,那梯子的底端滑动多少米?
一、复习回顾
解:由勾股定理知,滑动前梯子底端距墙6 m
设梯子底端滑动x m,那么滑动后梯子底端距墙(6+x)m
72+(x+6)2=102
本章开始时梯子下滑的问题:.
如图,一个长为10m的梯子斜靠在墙上,梯子顶端距地面的垂直距离为8m.
(2)梯子顶端下滑几米时,梯子底端滑动的距离和它相等呢?
一、复习回顾
(8-x)2+(x+6)2=102
设梯子顶端下滑x m,梯子底端滑动(6+x)m,得
解:由勾股定理知,滑动前梯子底端距墙6 m
本章开始时梯子下滑的问题:.
(3)如果梯子的长度是 13 m,梯子顶端与地面的垂直距离为 12 m,那么梯子顶端下滑的距离与梯子的底端滑动的距离可能相等吗?如果相等,那么这个距离是多少?
一、复习回顾
(12-x)2+(x+5)2=132
设梯子顶端下滑x m,那么滑动后梯子底端距墙(5+x)m
解:由勾股定理知,滑动前梯子底端距墙5 m
如图,某海军基地位于点A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰从A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
A
B
D
C
E
F
北
东
已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里 (结果精确到0.1海里)
二、探究新知
(一)审清题意,找等量关系
分析:由题意得 ,AB=BC=200 海里,∠ABC=90°
D是AC的中点,F是BC的中点,连接DF,
则DF是△ABC的中位线,DF=100海里,BF=100海里
V军舰= 2V补给船
军舰与补给船相遇于E处
∴ S军舰=AB+BE,S补给船=DE
∴ AB+BE = DE
EF2+DF2=DE2
北
东
A
B
C
D
E
F
100
二、探究新知
200
200
(二) 设未知数
解:设相遇时补给船所走路程DE为x 海里,
则军舰所走路程AB+BE的长为2x 海里,
AB+BF=300 海里,所以EF表示为(300-2x)海里
(三)列方程
在Rt△DFE中,由勾股定理,得
即 (300-2x)2+1002=x2 ,
北
东
A
B
C
D
E
F
100
二、探究新知
200
200
若设相遇时补给船的行程DE为x海里
连接DF.
∵AD=CD,BF=CF
∴DF是 ABC的中位线
∴DF∥AB,且DF= AB
∵AB⊥BC,AB=BC=200海里
∵DF⊥BC,DF=100海里,BF=100海里
∴EF=AB+BF-(AB+BE)=(300- 2x)海里 。
在Rt DEF中,根据勾股定理可得方程:
整理,得:
(舍去)
所以,相遇是补给船大约航行了118.4海里
解法一:
那么 DE= 海里,AB+BE= 海里
x
2x
北
东
A
B
C
D
E
F
北
东
解:连接DF.
∵AD=CD,BF=CF,
∴DF是△ABC的中位线.
∴DF∥AB,且DF= AB.
∵AB⊥BC,AB=BC=200 海里,
∴DF⊥BC,DF=100 海里, BF=100 海里.
设相遇时补给船航行了x 海里,那么
DE=x 海里, AB+BE=2x 海里,
EF=AB+BF-(AB+BE)=(300-2x) 海里.
解法二:
北
东
在Rt△DEF中,
根据勾股定理可得方程
整理,得
解这个方程,得
所以,相遇时补给船大约航行了118.4 海里.
与直角三角形有关的问题:直角三角形两直角边的平方和等于斜边的平方是这类问题的等量关系,即用勾股定理列方程.
归纳总结
《九章算术》“勾股”章中:“今有二人同所立.甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙各行几何 ”
大意是说:已知甲,乙二人同时从同一地点出发,甲的速度是7,乙
的速度是3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲,乙各走了多远
解:设甲,乙相遇时所用时间为x,根据题意,得
(7x - 10)2 = (3x) 2 +10 2.
整理得 2x2 - 7x = 0.
解方程,得 x1=3.5, x2=0 (不合题意,舍去).
∴3x=3×3.5 =10.5 , 7x = 7×3.5 = 24.5.
答:甲走了24.5步,乙走了10.5步.
O
东
北
A
B
10
3x
7x -10
如图,A,B,C,D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动.
(1)P,Q两点从出发开始到几秒?
四边形PBCQ的面积为33cm2;
(2)P,Q两点从出发开始到几秒时?
点P和点Q的距离是10cm.
例2:利用一元二次方程解决行程(动点)问题
解:(1)设P,Q两点运动x秒时四边形PBCQ的面积为33cm2,
则PB=(16-3x)cm,QC=2x cm.根据梯形的面积
公式得 (16-3x+2x)×6=33,解得x=5.
(2)设P,Q两点从出发经过t秒时,
点P,Q间的距离是10cm,
如图,作QE⊥AB,垂足为E,
则QE=AD=6,PQ=10.∵PA=3t,CQ=BE=2t,
∴PE=AB-AP-BE= |16-5t| .
由勾股定理,得(16-5t)2+62=102,
解得t1=4.8,t2=1.6.
答:(1)P,Q两点从出发开始到5秒时四边形PBCQ的面积为33 cm2;
(2)从出发到1.6秒或4.8秒时,点P和点Q的距离是10 cm.
1.如图,在△ABC中,∠C=90°,AB=10 cm,AC=8 cm,点P,Q同时由A,C两点出发,分别沿AC,CB方向向点C,B移动,它们的速度都是2 cm/s,经过几秒,P,Q两点相距2 cm
巩固练习
解:设经过t s,P,Q两点相距2 cm.
∴CQ=AP=t,CP=8-2t
∵∠C=90°,∴CQ2+PC2=PQ2.
∴(2t)2+(8-2t)2=(2 )2.
∴4t2+64-32t+4t2=40.
化简,得t2-4t+3=0.
解得t1=1,t2=3.经检验,t1,t2均符合题意.
答:经过1 s或3 s,P,Q两点相距2 cm
1)关键—— 动中取静
把动的点进行转换,变为线段的长度,
2)方法—— 时间变路程
求“动点的运动时间”可以转化为求“动点的运动路程”,也是求线段的长度;
由此,学会把动点的问题转化为静点的问题,
是解这类问题的关键.
3)常找的数量关系——
面积,勾股定理,相似三角形等;
归纳总结
1.如图,AB⊥BC,AB=10 cm,BC=8 cm,一只蝉从C点沿CB方向以每秒1 cm的速度爬行,蝉开始爬行的同时,一只螳螂由A点沿AB方向以每秒2 cm的速度爬行,当螳螂和蝉爬行x秒后,它们分别到达了M,N的位置,此时,△MNB的面积恰好为24 cm2,由题意可列方程( )
A.2x·x=24
B.(10-2x)(8-x)=24
C.(10-x)(8-2x)=24
D.(10-2x)(8-x)=48
D
四、课堂检测
2. 公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花,原空地一边减少了1 m,另一边减少了2 m,剩余空地的面积为18 m2,求原正方形空地的边长. 设原正方形的空地的边长为x m,则可列方程为( )
A. (x+1)(x+2)=18 B. x2-3x+16=0
C. ( x-1)(x-2)=18 D. x2+3x+16=0
C
四、课堂检测
3. 如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm. 动点P,Q分别从点A,B同时开始移动,点P的速度为1cm/s,点Q的速度为2cm/s,点Q移动到点C后停止,点P也随之停止运动. 下列时间瞬间中,能使△PBQ的面积为15cm2的是( )
A. 第2秒钟 B. 第3秒钟
C. 第4秒钟 D. 第5秒钟
四、课堂检测
B
四、课堂检测
4.如图,某农场有一块长40 m,宽32 m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1 140m2,求小路的宽.
解:设小路的宽为x m,依题意,得
(40-x)(32-x)=1 140.
整理,得x2-72x+140=0.
解得x1=2,x2=70 (不合题意,舍去)
答:小路的宽是2 m.
5.如图,在矩形ABCD中,AB=6cm, BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,那么几秒后五边形APQCD的面积为64cm2?
A
B
C
D
Q
P
解:设所需时间为 t s,根据题意,得
2t (6 - t) ÷2 = 6×12 - 64.
整理得 t2 - 6t + 8 = 0.
解方程,得 t1 = 2 , t2 = 4 .
答:在第2秒和第4秒是五边形面积是 64cm2.
(6 - t)
2t
四、课堂检测
6.某农场要建一个长方形的养鸡场,养鸡场的一边靠墙(墙长为20米),另三边用总长40米的木栏围成.要使得围成的养鸡场的面积为198米2,三边木栏的长应分别为多少米?
解:设养鸡场的宽x米,则长为(40-2x)米,得:
(40-2x) x=198
解得:x1=9,x2=11
当x=9时,长=40-2x=40-18=22>20,不符合题意,舍去;
当x=11时,长=40-2x=40-22=18<20,符合题意;
答:养鸡场的长为18米,宽为11米.
四、课堂检测
7.如图,在Rt△ABC中,∠C=90°,AC=6m,BC=8m,
(1)点P、Q同时由A、B两点出发,分别沿AC、BC的方向向点C匀速运动(到点C为止),它们的速度都是1m/s.经过几秒△PCQ的面积等于Rt△ABC面积的一半?
四、课堂检测
解:设经过x秒△PCQ的面积等于Rt△ABC面积的一半
∴AP=BQ=x m,PC=(6-x) m,CQ=(8-x) cm
(6-x)(8-x)= × ×6×8
化简得:x2-14x+24=0
解得x1=2, x1=12(不符合题意,舍去)
答:经过2秒△PCQ的面积等于Rt△ABC面积的一半.
7.如图,在Rt△ABC中,∠C=90°,AC=6m,BC=8m,
(2)点P由A出发,沿AC方向匀速运动,当点P到达点C则停止运动,点Q同时由C出发,沿CB方向匀速运动,它们的速度都是1m/s .几秒后△PCQ的面积等于△ABC面积的 ?
四、课堂检测
解:设经过x秒△PCQ的面积等于Rt△ABC面积的∴AP=CQ=x m,PC=(6-x) m
x(6-x) = × ×6×8
化简得:x2-6x+8=0
解得x1=2, x1=4
答:经过2秒或4秒△PCQ的面积等于Rt△ABC面积的.
在列一元二次方程解应用题时,由于所得的根一般有两个,所以要检验这两个根是否符合实际问题的要求.
列一元二次方程解应用题的步骤:
审、设、列、解、检、答.
五、课堂小结
六、布置作业
课本P53 习题2.9 第1,2,3,4题
谢谢聆听
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
