北师大版九年级数学下册 2.5二次函数与一元二次方程同步练习 (含解析)
文档属性
| 名称 | 北师大版九年级数学下册 2.5二次函数与一元二次方程同步练习 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 556.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 16:08:27 | ||
图片预览



文档简介
北师大版九下 2.5 二次函数与一元二次方程
一、选择题(共13小题)
1. 抛物线 与 轴有两个不同的交点,则一元二次方程 的根的情况是
A. 有两个不同的实数根 B. 有两个相同的实数根
C. 没有实数根 D. 无法判定
2. 下列抛物线与 轴无交点的是
A. B. C. D.
3. 下面的表格是一个二次函数 的自变量 和函数 的部分对应值:
这个二次函数与坐标轴为交点的个数为
A. B. C. D.
4. 下列表格给出的是二次函数 的几组对应值,那么方程 的一个解的取值范围是
A. B. C. D. 不能确定
5. 二次函数 的图象如图所示,现有以下结论:
():
();
(),
();
();
其中正确的结论有
A. 个 B. 个 C. 个 D. 个
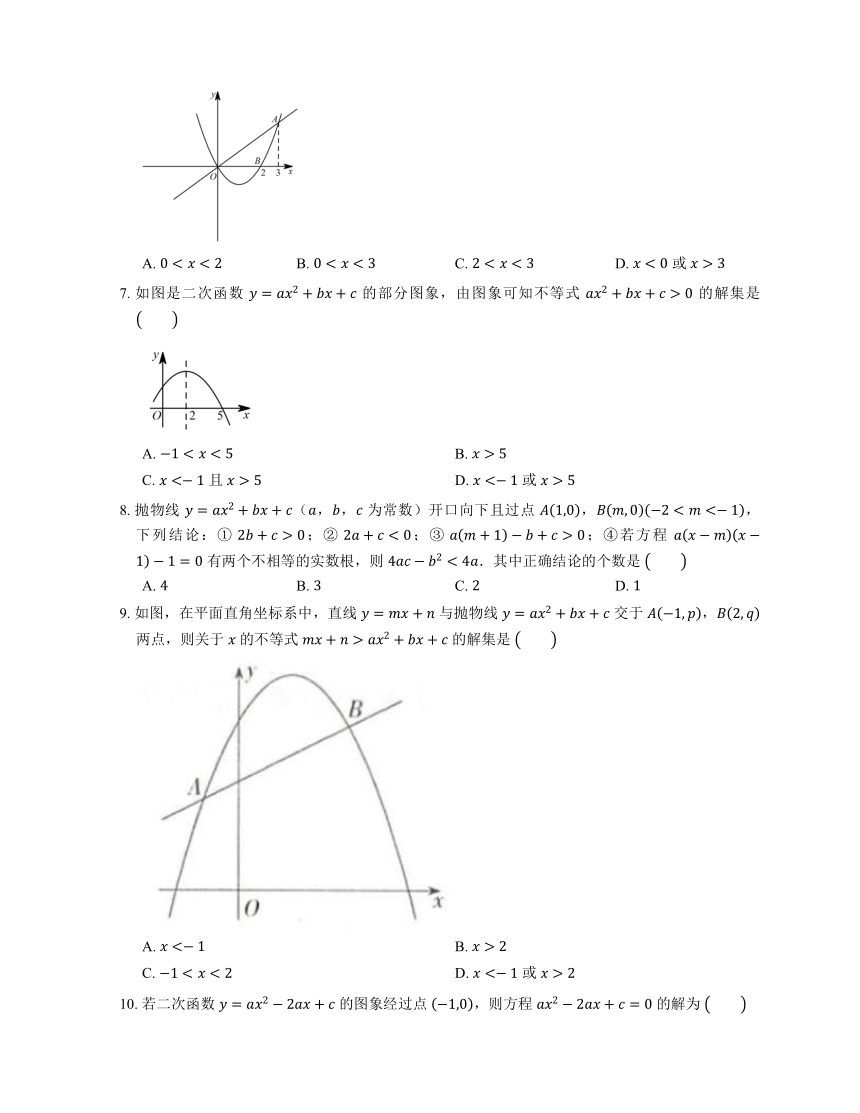
6. 如图,已知二次函数 的图象与正比例函数 的图象交于点 ,与 轴交于点 ,若 ,则 的取值范围是
A. B. C. D. 或
7. 如图是二次函数 的部分图象,由图象可知不等式 的解集是
A. B.
C. 且 D. 或
8. 抛物线 (,, 为常数)开口向下且过点 ,,下列结论:① ;② ;③ ;④若方程 有两个不相等的实数根,则 .其中正确结论的个数是
A. B. C. D.
9. 如图,在平面直角坐标系中,直线 与抛物线 交于 , 两点,则关于 的不等式 的解集是
A. B.
C. D. 或
10. 若二次函数 的图象经过点 ,则方程 的解为
A. , B. ,
C. , D. ,
11. 二次函数 (,, 为常数,且 中的 与 的部分对应值如下表:
下列结论:
① ;
②当 时, 的值随 值的增大而减小;
③ 是方程 的一个根;
④当 时,.
其中正确的个数为
A. 个 B. 个 C. 个 D. 个
12. 二次函数 ()和正比例函数 的图象如图所示,则方程 ()的两根之和
A. 大于 B. 等于 C. 小于 D. 不能确定
13. 二次函数 (,, 是常数,)的自变量 与函数值 的部分对应值如下表:
且当 时,与其对应的函数值 .有下列结论:
① ;② 和 是关于 的方程 的两个根;③ .
其中,正确结论的个数是
A. B. C. D.
二、填空题(共5小题)
14. 下图是抛物线 和一次函数 的图象,观察图象写出 时, 的取值范围 .
15. 已知函数 ,若使 成立的 值恰好有 个,则 的值为 .
16. 对于一个函数,自变量 取 时,函数值 也等于 ,我们称 为这个函数的不动点.如果二次函数 有两个相异的不动点 ,,且 ,则 的取值范围是 .
17. 关于抛物线 ,给出下列结论:
①当 时,抛物线与直线 没有交点;
②若抛物线与 轴有两个交点,则其中一定有一个交点在点 与 之间;
③若抛物线的顶点在点 ,, 所围成的三角形区域内(包括边界),则 .其中正确结论的序号是 .
18. 已知二次函数 ( 为常数),当 时,函数 有最小值 ,则 的值为 .
三、解答题(共7小题)
19. 已知二次函数 ( 为常数,且 ).
(1)求证:不论 为何值,该函数的图象与 轴总有公共点;
(2)设该函数的图象与 轴交于点 ,若点 在 轴上方,求 的取值范围;
(3)该函数图象所过的象限随 的值变化而变化,直接写出函数图象所经过的象限及对应的 的取值范围.
20. 已知关于 的二次函数 的图象的顶点 和其上一点 的坐标,求这个二次函数的解析式.
(1),.
(2),.
21. 已知抛物线 ( 为常数,且 ).
(1)求证:抛物线与 轴有两个公共点;
(2)设抛物线与 轴的两个公共点分别为 ,( 在 左侧),与 轴的交点为 .当 时,求抛物线的表达式.
22. 在平面直角坐标系中,设二次函数 ,其中 .
(1)若函数 的图象经过点 ,求函数 的解析式;
(2)若抛物线与 轴的两交点坐标为 ,( 点在 点的左侧),与 轴的交点为 ,满足 时,求 的值.
(3)已知点 和 在函数 的图象上,若 ,求 的取值范围.
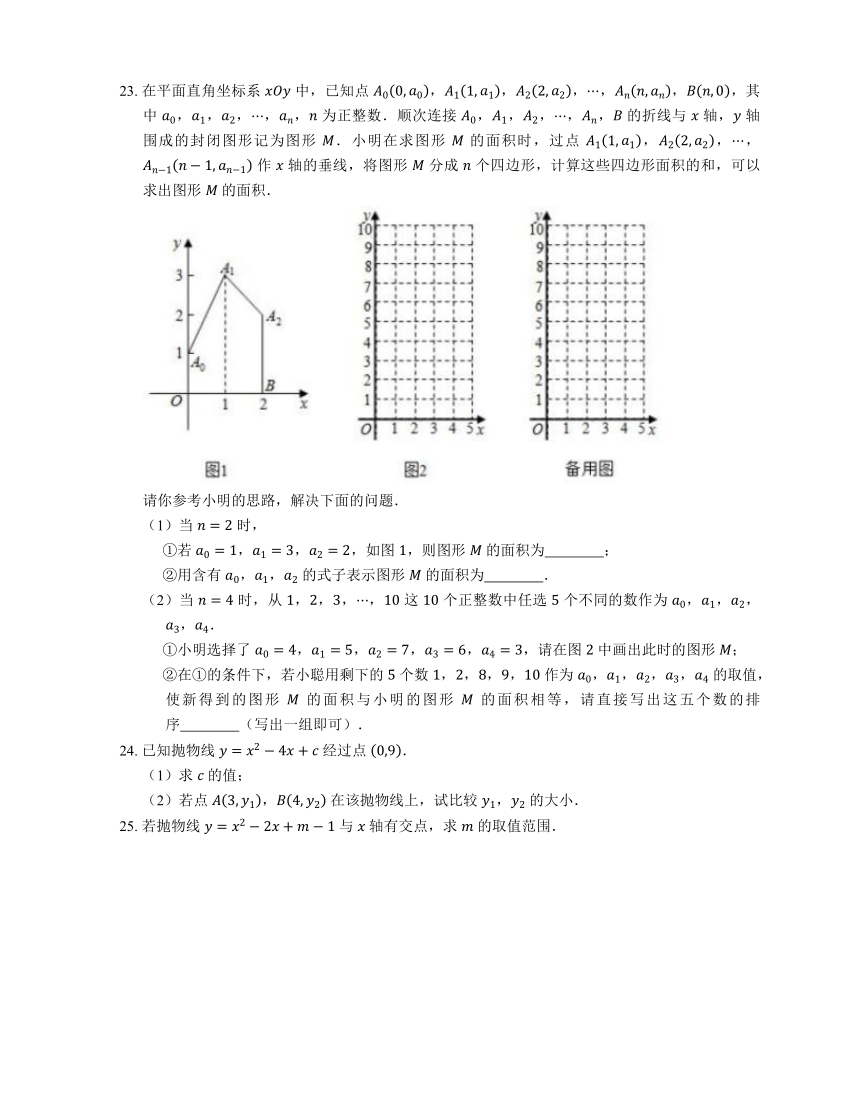
23. 在平面直角坐标系 中,已知点 ,,,,,,其中 ,,,,, 为正整数.顺次连接 ,,,,, 的折线与 轴, 轴围成的封闭图形记为图形 .小明在求图形 的面积时,过点 ,,, 作 轴的垂线,将图形 分成 个四边形,计算这些四边形面积的和,可以求出图形 的面积.
请你参考小明的思路,解决下面的问题.
(1)当 时,
①若 ,,,如图 ,则图形 的面积为 ;
②用含有 ,, 的式子表示图形 的面积为 .
(2)当 时,从 ,,,, 这 个正整数中任选 个不同的数作为 ,,,,.
①小明选择了 ,,,,,请在图 中画出此时的图形 ;
②在①的条件下,若小聪用剩下的 个数 ,,,, 作为 ,,,, 的取值,使新得到的图形 的面积与小明的图形 的面积相等,请直接写出这五个数的排序 (写出一组即可).
24. 已知抛物线 经过点 .
(1)求 的值;
(2)若点 , 在该抛物线上,试比较 , 的大小.
25. 若抛物线 与 轴有交点,求 的取值范围.
答案
1. A
2. B
3. D
4. B
5. C
【解析】() 函数开口向下,
,
对称轴在 轴的右边,
,
,故命题正确;
(),,,
,故命题正确;
() 当 时,,
,故命题错误;
() 当 时,,
,故命题正确;
() 抛物线与 轴于两个交点,
,故命题正确.
6. B
【解析】若 ,则二次函数图象在一次函数图象的下面,此时 的取值范围是 .
7. A
【解析】由图象可知,抛物线与 轴的一个交点为 ,对称轴是 ,
根据抛物线的对称性可知抛物线与 轴的另一个交点的坐标为 .由图象看出当 时,函数图象在 轴上方,所以不等式 的解集是 .
8. A
【解析】根据题意得 ,
,
当 时,有 ,
,
,
②正确,
由 ,得 ,
,
,
①正确,
由 得 ,
当 时,,
而 ,,
,
③正确,
若方程 有两个不相等的实数根,
即 有两个不相等的实数根,
顶点的纵坐标 ,
,
④正确.
9. D
【解析】观察题图可知,当 或 时,直线 在拋物线 的上方,
不等式 的解集为 或 .
10. C
【解析】因为二次函数 的图象经过点 ,
所以方程 一定有一个解为:,
因为抛物线的对称轴为:直线 ,
所以二次函数 的图象与 轴的另一个交点为:,
所以方程 的解为:,.
11. B
【解析】由数据分析可知 ,,
,①正确;
对称轴 ,当 时, 随 的增大而减小,②错误;
时,,
.
,
,③正确;
时,,
时,.
时, 且函数有最大值,
当 时,,④正确.
12. A
13. C
14.
15. 或
16.
【解析】由题意知二次函数 的两个相异的不动点 , 是方程 的两个不相等实数根,
且 ,
整理,得:,
由 有两个不相等的实数根,且 ,
知 ,
令 ,画出该二次函数的草图如下:
则
解得 .
17. ②③
18.
【解析】 二次函数 ,当 时,函数 有最小值 ,
当 时, 时取得最小值,,得 (舍去).
当 时, 时取得最小值,,得 (舍去),(舍去);
当 时, 时取得最小值,,得 .
由上可得, 的值是 .
19. (1) 当 时,,
解得 ,,
当 ,即 时,方程有两个相等的实数根;
当 ,即 时,方程有两个不相等的实数根,
不论 为何值,该函数的图象与 轴总有公共点.
(2) 当 时,,
点 的纵坐标为 ,
该函数的图象与 轴交于点 ,点 在 轴上方,
.
设 ,即 是 的二次函数,
当 时,.
抛物线开口向上,
当 或 时,.
的取值范围是 或 .
(3) ①当 时,图象经过一、二、四象限;
②当 或 时,图象经过一、三、四象限;
③当 时,图象经过三、四象限;
④当 时,图象经过一、二、三、四象限.
【解析】根据()()两问,可得:
①当 时,开口向上,与 轴交点的横坐标:,,此时图象经过一、二、四象限;
②当 或 时,开口向下,与 轴交点的横坐标:,,此时图象经过一、三、四象限;
③当 时,开口向下,与 轴交点的横坐标为 ,此时图象经过三、四象限;
④当 时,开口向下,与 轴交点的横坐标为:,,此时图象经过一、二、三、四象限.
20. (1) .
(2) .
21. (1)
,
.
抛物线与 轴有两个公共点.
(2) .
化简得 .
解得 ,或 .
,.
由 可得 .
.
.
解得 .
.
22. (1) 函数 的图象经过点 ,得
,
整理,得 ,
解得 ,,
函数 的表达式 ,化简,得 ;
函数 的表达式 化简,得 ,
综上所述:函数 的表达式 ;
(2) 当 时 ,
整理,得
,
解得 ,,
的图象与 轴的交点是 ,,
当 时,.即 ,
,
,
,
,
整理,得
,
,
解得 ,(舍去).
(3) 当 在对称轴的左侧(含顶点)时, 随 的增大而减小,
与 关于对称轴对称,
由 ,得 ;
当时 在对称轴的右侧时, 随 的增大而增大,
由 ,得 ,
综上所述:,所求 的取值范围 .
23. (1) ① ;② .
【解析】①如图 所示,
过点 ,作 于 ,
②同样可得图形 的面积 .
(2) ①如图 所示:
② ,,,,(答案不唯一)
【解析】②如图 所示,
小明的图形 的面积 ,
新图形 的面积 .
新得到的图形 的面积与小明的图形 的面积相等.
24. (1) 当 时,,
的值为 .
(2) 由()可知抛物线的表达式为 ,
当 时,;
当 时,.
,
.
25. .
一、选择题(共13小题)
1. 抛物线 与 轴有两个不同的交点,则一元二次方程 的根的情况是
A. 有两个不同的实数根 B. 有两个相同的实数根
C. 没有实数根 D. 无法判定
2. 下列抛物线与 轴无交点的是
A. B. C. D.
3. 下面的表格是一个二次函数 的自变量 和函数 的部分对应值:
这个二次函数与坐标轴为交点的个数为
A. B. C. D.
4. 下列表格给出的是二次函数 的几组对应值,那么方程 的一个解的取值范围是
A. B. C. D. 不能确定
5. 二次函数 的图象如图所示,现有以下结论:
():
();
(),
();
();
其中正确的结论有
A. 个 B. 个 C. 个 D. 个
6. 如图,已知二次函数 的图象与正比例函数 的图象交于点 ,与 轴交于点 ,若 ,则 的取值范围是
A. B. C. D. 或
7. 如图是二次函数 的部分图象,由图象可知不等式 的解集是
A. B.
C. 且 D. 或
8. 抛物线 (,, 为常数)开口向下且过点 ,,下列结论:① ;② ;③ ;④若方程 有两个不相等的实数根,则 .其中正确结论的个数是
A. B. C. D.
9. 如图,在平面直角坐标系中,直线 与抛物线 交于 , 两点,则关于 的不等式 的解集是
A. B.
C. D. 或
10. 若二次函数 的图象经过点 ,则方程 的解为
A. , B. ,
C. , D. ,
11. 二次函数 (,, 为常数,且 中的 与 的部分对应值如下表:
下列结论:
① ;
②当 时, 的值随 值的增大而减小;
③ 是方程 的一个根;
④当 时,.
其中正确的个数为
A. 个 B. 个 C. 个 D. 个
12. 二次函数 ()和正比例函数 的图象如图所示,则方程 ()的两根之和
A. 大于 B. 等于 C. 小于 D. 不能确定
13. 二次函数 (,, 是常数,)的自变量 与函数值 的部分对应值如下表:
且当 时,与其对应的函数值 .有下列结论:
① ;② 和 是关于 的方程 的两个根;③ .
其中,正确结论的个数是
A. B. C. D.
二、填空题(共5小题)
14. 下图是抛物线 和一次函数 的图象,观察图象写出 时, 的取值范围 .
15. 已知函数 ,若使 成立的 值恰好有 个,则 的值为 .
16. 对于一个函数,自变量 取 时,函数值 也等于 ,我们称 为这个函数的不动点.如果二次函数 有两个相异的不动点 ,,且 ,则 的取值范围是 .
17. 关于抛物线 ,给出下列结论:
①当 时,抛物线与直线 没有交点;
②若抛物线与 轴有两个交点,则其中一定有一个交点在点 与 之间;
③若抛物线的顶点在点 ,, 所围成的三角形区域内(包括边界),则 .其中正确结论的序号是 .
18. 已知二次函数 ( 为常数),当 时,函数 有最小值 ,则 的值为 .
三、解答题(共7小题)
19. 已知二次函数 ( 为常数,且 ).
(1)求证:不论 为何值,该函数的图象与 轴总有公共点;
(2)设该函数的图象与 轴交于点 ,若点 在 轴上方,求 的取值范围;
(3)该函数图象所过的象限随 的值变化而变化,直接写出函数图象所经过的象限及对应的 的取值范围.
20. 已知关于 的二次函数 的图象的顶点 和其上一点 的坐标,求这个二次函数的解析式.
(1),.
(2),.
21. 已知抛物线 ( 为常数,且 ).
(1)求证:抛物线与 轴有两个公共点;
(2)设抛物线与 轴的两个公共点分别为 ,( 在 左侧),与 轴的交点为 .当 时,求抛物线的表达式.
22. 在平面直角坐标系中,设二次函数 ,其中 .
(1)若函数 的图象经过点 ,求函数 的解析式;
(2)若抛物线与 轴的两交点坐标为 ,( 点在 点的左侧),与 轴的交点为 ,满足 时,求 的值.
(3)已知点 和 在函数 的图象上,若 ,求 的取值范围.
23. 在平面直角坐标系 中,已知点 ,,,,,,其中 ,,,,, 为正整数.顺次连接 ,,,,, 的折线与 轴, 轴围成的封闭图形记为图形 .小明在求图形 的面积时,过点 ,,, 作 轴的垂线,将图形 分成 个四边形,计算这些四边形面积的和,可以求出图形 的面积.
请你参考小明的思路,解决下面的问题.
(1)当 时,
①若 ,,,如图 ,则图形 的面积为 ;
②用含有 ,, 的式子表示图形 的面积为 .
(2)当 时,从 ,,,, 这 个正整数中任选 个不同的数作为 ,,,,.
①小明选择了 ,,,,,请在图 中画出此时的图形 ;
②在①的条件下,若小聪用剩下的 个数 ,,,, 作为 ,,,, 的取值,使新得到的图形 的面积与小明的图形 的面积相等,请直接写出这五个数的排序 (写出一组即可).
24. 已知抛物线 经过点 .
(1)求 的值;
(2)若点 , 在该抛物线上,试比较 , 的大小.
25. 若抛物线 与 轴有交点,求 的取值范围.
答案
1. A
2. B
3. D
4. B
5. C
【解析】() 函数开口向下,
,
对称轴在 轴的右边,
,
,故命题正确;
(),,,
,故命题正确;
() 当 时,,
,故命题错误;
() 当 时,,
,故命题正确;
() 抛物线与 轴于两个交点,
,故命题正确.
6. B
【解析】若 ,则二次函数图象在一次函数图象的下面,此时 的取值范围是 .
7. A
【解析】由图象可知,抛物线与 轴的一个交点为 ,对称轴是 ,
根据抛物线的对称性可知抛物线与 轴的另一个交点的坐标为 .由图象看出当 时,函数图象在 轴上方,所以不等式 的解集是 .
8. A
【解析】根据题意得 ,
,
当 时,有 ,
,
,
②正确,
由 ,得 ,
,
,
①正确,
由 得 ,
当 时,,
而 ,,
,
③正确,
若方程 有两个不相等的实数根,
即 有两个不相等的实数根,
顶点的纵坐标 ,
,
④正确.
9. D
【解析】观察题图可知,当 或 时,直线 在拋物线 的上方,
不等式 的解集为 或 .
10. C
【解析】因为二次函数 的图象经过点 ,
所以方程 一定有一个解为:,
因为抛物线的对称轴为:直线 ,
所以二次函数 的图象与 轴的另一个交点为:,
所以方程 的解为:,.
11. B
【解析】由数据分析可知 ,,
,①正确;
对称轴 ,当 时, 随 的增大而减小,②错误;
时,,
.
,
,③正确;
时,,
时,.
时, 且函数有最大值,
当 时,,④正确.
12. A
13. C
14.
15. 或
16.
【解析】由题意知二次函数 的两个相异的不动点 , 是方程 的两个不相等实数根,
且 ,
整理,得:,
由 有两个不相等的实数根,且 ,
知 ,
令 ,画出该二次函数的草图如下:
则
解得 .
17. ②③
18.
【解析】 二次函数 ,当 时,函数 有最小值 ,
当 时, 时取得最小值,,得 (舍去).
当 时, 时取得最小值,,得 (舍去),(舍去);
当 时, 时取得最小值,,得 .
由上可得, 的值是 .
19. (1) 当 时,,
解得 ,,
当 ,即 时,方程有两个相等的实数根;
当 ,即 时,方程有两个不相等的实数根,
不论 为何值,该函数的图象与 轴总有公共点.
(2) 当 时,,
点 的纵坐标为 ,
该函数的图象与 轴交于点 ,点 在 轴上方,
.
设 ,即 是 的二次函数,
当 时,.
抛物线开口向上,
当 或 时,.
的取值范围是 或 .
(3) ①当 时,图象经过一、二、四象限;
②当 或 时,图象经过一、三、四象限;
③当 时,图象经过三、四象限;
④当 时,图象经过一、二、三、四象限.
【解析】根据()()两问,可得:
①当 时,开口向上,与 轴交点的横坐标:,,此时图象经过一、二、四象限;
②当 或 时,开口向下,与 轴交点的横坐标:,,此时图象经过一、三、四象限;
③当 时,开口向下,与 轴交点的横坐标为 ,此时图象经过三、四象限;
④当 时,开口向下,与 轴交点的横坐标为:,,此时图象经过一、二、三、四象限.
20. (1) .
(2) .
21. (1)
,
.
抛物线与 轴有两个公共点.
(2) .
化简得 .
解得 ,或 .
,.
由 可得 .
.
.
解得 .
.
22. (1) 函数 的图象经过点 ,得
,
整理,得 ,
解得 ,,
函数 的表达式 ,化简,得 ;
函数 的表达式 化简,得 ,
综上所述:函数 的表达式 ;
(2) 当 时 ,
整理,得
,
解得 ,,
的图象与 轴的交点是 ,,
当 时,.即 ,
,
,
,
,
整理,得
,
,
解得 ,(舍去).
(3) 当 在对称轴的左侧(含顶点)时, 随 的增大而减小,
与 关于对称轴对称,
由 ,得 ;
当时 在对称轴的右侧时, 随 的增大而增大,
由 ,得 ,
综上所述:,所求 的取值范围 .
23. (1) ① ;② .
【解析】①如图 所示,
过点 ,作 于 ,
②同样可得图形 的面积 .
(2) ①如图 所示:
② ,,,,(答案不唯一)
【解析】②如图 所示,
小明的图形 的面积 ,
新图形 的面积 .
新得到的图形 的面积与小明的图形 的面积相等.
24. (1) 当 时,,
的值为 .
(2) 由()可知抛物线的表达式为 ,
当 时,;
当 时,.
,
.
25. .
