有理数的乘法[上学期]
图片预览






文档简介
课件14张PPT。 授课人:干江中学李土青
2005-9-21有理数的乘法实例:如下图所示,一只蜗牛沿直线L爬行,它的位置恰好在L上的O点。
1.如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟后它在什么位置?
2.如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟后它在什么位置?
3.如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
4.如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟前它在什么位置?分析:以上四个问题涉及两组相反的量:向右和向左爬行、
3分钟后和3分钟前,为了区分方向,不防规定:
向右为正,向左为负,为区分时间,我们规定:
现在后为正,现在前为负。
1.如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置? 首先,我们应该知道这里的“2cm”记作“+ 2cm”, “3分钟后”记作“+ 3分钟”
用一个运算式来表示就是:(+ 2) ×(+3)2.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?首先,我们应该知道这里的“2cm”记作“- 2cm”, “3分钟后”记作“+ 3分钟”
用一个运算式来表示就是:(-2) ×(+3)
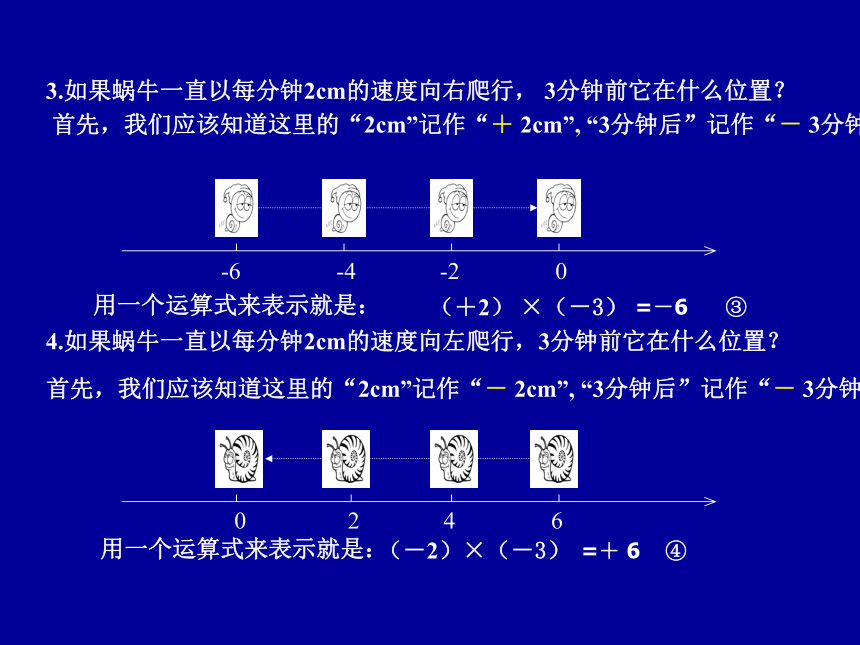
=+6 ①=-6 ②3.如果蜗牛一直以每分钟2cm的速度向右爬行, 3分钟前它在什么位置? 首先,我们应该知道这里的“2cm”记作“+ 2cm”, “3分钟后”记作“- 3分钟”
用一个运算式来表示就是:
(+2) ×(-3)
4.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?首先,我们应该知道这里的“2cm”记作“- 2cm”, “3分钟后”记作“- 3分钟”
用一个运算式来表示就是: (-2)×(-3)=-6 ③=+ 6 ④由刚才的这四个问题我们就得到了下面四个算术式:
(+ 2) ×(+ 3)= + 6 ①
(- 2) ×(+ 3)= - 6 ②
(+ 2) ×(- 3)= - 6 ③
(-2 ) ×(- 3)= + 6 ④
归纳:两个有理数相乘,积仍然由符号和绝对值两部分组成。
①、④两式都是同号两数相乘,积为正;
②、③两式都是异号两数相乘,积为负;
①—④四式中的积的绝对值都是这两个因数绝对值的积。也就是:两数相乘,同号得正,异号得负,并把绝对值相乘。也就是:任何数同零相乘,都得零。有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。例一:(-5) ×( -3)………… 同号两数相乘 (-5) ×( -3)= +( ) ,………… 得正 5 × 3 = 15 ,
………… 把绝对值相乘所以:(-5) ×( -3)= +(5 ×3)= +15
异号两数相乘得负把绝对值相乘 进行有理数的乘法运算,关键是积的符号的确定,计算时分两步进行。
第一步:确定积的符号,在确定积的符号时要准确运用法则;
第二步:求绝对值的积。(1)(-0.7)× 2.3 = (2) 6 ×(-3)=
(3) 0 ×(-3)= (4)(-3) × 0 =
(5) 0.5 × 2 = (6)(-0.5)×(-2)=-1.61-180+1注意:小学里我们知道,乘积为1的两个数互为倒数。
现在我们仍然是: 乘积为1的两个数互为倒数。01+倒 数 和 相 反 数 有 什么异同?相同点:它们都是成对出现的。
不同点:①互为相反数的两个数和为0; 互为倒数的两个数积为1。
②正数的相反数是负数, 正数的倒数是正数;
负数的相反数是正数, 负数的倒数是负数;
零的相反数是零, 零没有倒数。想一想:牛刀小试:例3、用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km气温的变化量为-6℃,攀登3km后,气温有什么变化?用一用:解:-6 ×3答:气温下降18 ℃=-18做一做
1.计算:
(1) 6 ×(- 9); (2)( - 4 )× 6; (3)(- 6)× (- 1);
(4) (-6) × 0 ;(5) ; (6) 。
3.写出下列各数的倒数:
1 , -1 , , ,5 , -5 , , 。
4.商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数 的商品相比,销售有什么变化?
2.下列计算是否正确?为什么?
(1)-2×(-3)×4 = 24
(2)-5+(-3) = 8
(3)(-6)×(0.2) = -1.2
(4)(+8)+(-3) = -5
(5)(-4)×(+10) = 401.有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。
2. 倒数的定义
家庭作业:书本习题1.4第1,2,3题小结:乘积是1的两个数互为倒数。试一试:你能举一个实例,使列出的算式是-3 ×5=-15吗?再见谢谢大家
2005-9-21有理数的乘法实例:如下图所示,一只蜗牛沿直线L爬行,它的位置恰好在L上的O点。
1.如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟后它在什么位置?
2.如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟后它在什么位置?
3.如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
4.如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟前它在什么位置?分析:以上四个问题涉及两组相反的量:向右和向左爬行、
3分钟后和3分钟前,为了区分方向,不防规定:
向右为正,向左为负,为区分时间,我们规定:
现在后为正,现在前为负。
1.如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置? 首先,我们应该知道这里的“2cm”记作“+ 2cm”, “3分钟后”记作“+ 3分钟”
用一个运算式来表示就是:(+ 2) ×(+3)2.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?首先,我们应该知道这里的“2cm”记作“- 2cm”, “3分钟后”记作“+ 3分钟”
用一个运算式来表示就是:(-2) ×(+3)
=+6 ①=-6 ②3.如果蜗牛一直以每分钟2cm的速度向右爬行, 3分钟前它在什么位置? 首先,我们应该知道这里的“2cm”记作“+ 2cm”, “3分钟后”记作“- 3分钟”
用一个运算式来表示就是:
(+2) ×(-3)
4.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?首先,我们应该知道这里的“2cm”记作“- 2cm”, “3分钟后”记作“- 3分钟”
用一个运算式来表示就是: (-2)×(-3)=-6 ③=+ 6 ④由刚才的这四个问题我们就得到了下面四个算术式:
(+ 2) ×(+ 3)= + 6 ①
(- 2) ×(+ 3)= - 6 ②
(+ 2) ×(- 3)= - 6 ③
(-2 ) ×(- 3)= + 6 ④
归纳:两个有理数相乘,积仍然由符号和绝对值两部分组成。
①、④两式都是同号两数相乘,积为正;
②、③两式都是异号两数相乘,积为负;
①—④四式中的积的绝对值都是这两个因数绝对值的积。也就是:两数相乘,同号得正,异号得负,并把绝对值相乘。也就是:任何数同零相乘,都得零。有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。例一:(-5) ×( -3)………… 同号两数相乘 (-5) ×( -3)= +( ) ,………… 得正 5 × 3 = 15 ,
………… 把绝对值相乘所以:(-5) ×( -3)= +(5 ×3)= +15
异号两数相乘得负把绝对值相乘 进行有理数的乘法运算,关键是积的符号的确定,计算时分两步进行。
第一步:确定积的符号,在确定积的符号时要准确运用法则;
第二步:求绝对值的积。(1)(-0.7)× 2.3 = (2) 6 ×(-3)=
(3) 0 ×(-3)= (4)(-3) × 0 =
(5) 0.5 × 2 = (6)(-0.5)×(-2)=-1.61-180+1注意:小学里我们知道,乘积为1的两个数互为倒数。
现在我们仍然是: 乘积为1的两个数互为倒数。01+倒 数 和 相 反 数 有 什么异同?相同点:它们都是成对出现的。
不同点:①互为相反数的两个数和为0; 互为倒数的两个数积为1。
②正数的相反数是负数, 正数的倒数是正数;
负数的相反数是正数, 负数的倒数是负数;
零的相反数是零, 零没有倒数。想一想:牛刀小试:例3、用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km气温的变化量为-6℃,攀登3km后,气温有什么变化?用一用:解:-6 ×3答:气温下降18 ℃=-18做一做
1.计算:
(1) 6 ×(- 9); (2)( - 4 )× 6; (3)(- 6)× (- 1);
(4) (-6) × 0 ;(5) ; (6) 。
3.写出下列各数的倒数:
1 , -1 , , ,5 , -5 , , 。
4.商店降价销售某种商品,每件降5元,售出60件后,与按原价销售同样数 的商品相比,销售有什么变化?
2.下列计算是否正确?为什么?
(1)-2×(-3)×4 = 24
(2)-5+(-3) = 8
(3)(-6)×(0.2) = -1.2
(4)(+8)+(-3) = -5
(5)(-4)×(+10) = 401.有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。
2. 倒数的定义
家庭作业:书本习题1.4第1,2,3题小结:乘积是1的两个数互为倒数。试一试:你能举一个实例,使列出的算式是-3 ×5=-15吗?再见谢谢大家
