第四章 一次函数综合测评题(含答案)
文档属性
| 名称 | 第四章 一次函数综合测评题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 426.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 20:47:24 | ||
图片预览


文档简介
PAGE
第四章 一次函数综合测评
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列函数中是一次函数的是( )
A. B. C. D.
2.直线y=x 4与y轴的交点坐标是( )
A.(-4,0) B.(4,0) C.(0,-4) D.(0,4)
3.下列表示y与x之间关系的图象中,y不是x的函数的是( )
A B C D
4.为了体现尊老、爱老的中华传统美德,重阳节当天学校组织若干名离、退休老教师去“开原市白鹭洲景区”旅游,已知共有y人参加此次重阳节旅游活动,若学校租37座的客车x辆,剩余8人无座位,则y与x之间的关系式为( )
A.y=8x+37 B.y=x+45 C.y=37x-8 D.y=37x+8
5.若ab<0且a>b,则函数y=ax+b的图象大致是( )
A B C D
6.用描点法画一次函数的图象,在如下表格中有一组数据错误,这组错误的数据是( )
A.(-2,12) B.(-1,11) C.(1,10) D.(2,8)
x -2 -1 1 2
y 12 11 10 8
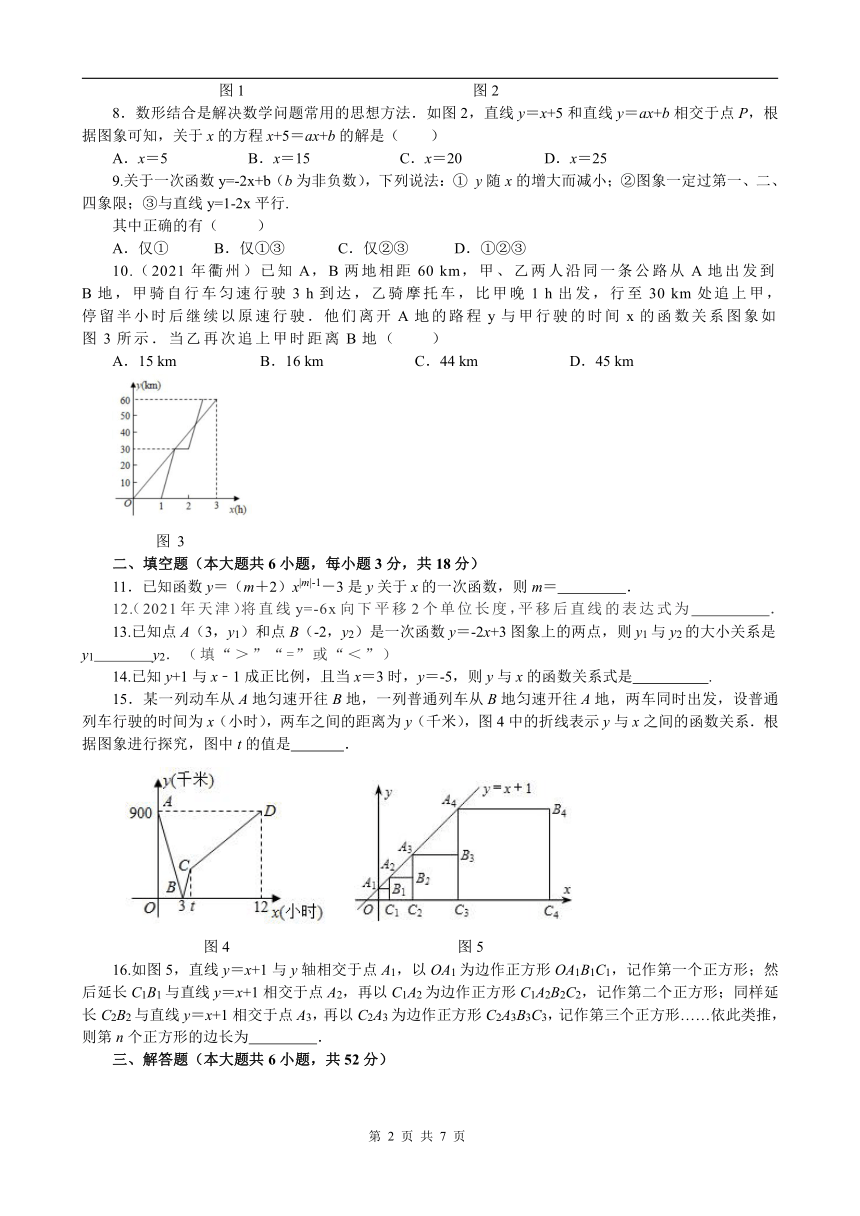
7.根据图1所示的程序计算函数y的值,若输入的x的值是-3和4时,输出的y值相等,则m等于( )
A.-17 B.-25 C.25 D.-43
图1 图2
8.数形结合是解决数学问题常用的思想方法.如图2,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,关于x的方程x+5=ax+b的解是( )
A.x=5 B.x=15 C.x=20 D.x=25
9.关于一次函数y=-2x+b(b为非负数),下列说法:① y随x的增大而减小;②图象一定过第一、二、四象限;③与直线y=1-2x平行.
其中正确的有( )
A.仅① B.仅①③ C.仅②③ D.①②③
10.(2021年衢州)已知A,B两地相距60 km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3 h到达,乙骑摩托车,比甲晚1 h出发,行至30 km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶的时间x的函数关系图象如图3所示.当乙再次追上甲时距离B地( )
A.15 km B.16 km C.44 km D.45 km
图3
二、填空题(本大题共6小题,每小题3分,共18分)
11.已知函数y=(m+2)x|m|-1-3是y关于x的一次函数,则m= .
12.(2021年天津)将直线y=-6x向下平移2个单位长度,平移后直线的表达式为 .
13.已知点A(3,y1)和点B(-2,y2)是一次函数y=-2x+3图象上的两点,则y1与y2的大小关系是y1 y2.(填“>”“=”或“<”)
14.已知y+1与x﹣1成正比例,且当x=3时,y=-5,则y与x的函数关系式是 .
15.某一列动车从A地匀速开往B地,一列普通列车从B地匀速开往A地,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图4中的折线表示y与x之间的函数关系.根据图象进行探究,图中t的值是 .
图4 图5
16.如图5,直线y=x+1与y轴相交于点A1,以OA1为边作正方形OA1B1C1,记作第一个正方形;然后延长C1B1与直线y=x+1相交于点A2,再以C1A2为边作正方形C1A2B2C2,记作第二个正方形;同样延长C2B2与直线y=x+1相交于点A3,再以C2A3为边作正方形C2A3B3C3,记作第三个正方形……依此类推,则第n个正方形的边长为 .
解答题(本大题共6小题,共52分)
17.(6分)已知y与x成正比例,且当x=2时,y=4.
(1)求y与x的函数关系式;
(2)当x=时,求y的值.
18.(8分)周末,小峰骑单车到图书馆,他骑行一段时间后,发现钥匙没在,于是原路返回.在等红绿灯的路口处找到了钥匙,便继续前往图书馆.小峰离家的距离与离家时间的关系如图6所示,请根据图中提供的信息回答下列问题:
(1)图中的自变量是 ;
(2)小峰本次去图书馆一共用了 分钟,在骑行过程中最快的速度是 米/分;
(3)求:小峰本次去图书馆一共骑行了多少米?
图6
19.(8分)已知一次函数y=2x-6,
(1)在图7中画出该函数的图象;
(2)判断(4,3)是否在此函数的图象上;
(3)观察画出的图象,说一说当x为何值时y<0?
图7
20.(8分)如图8,已知点A(6,0),点B(0,2).
(1)求直线AB的函数表达式;
(2)若C为直线AB上一动点,当△OBC的面积为3时,试求点C的坐标.
图8
21.(10分)某工厂生产某种产品,每件产品的成本价为25元,出厂价为50元.在生产过程中,每件产品产生0.5立方米污水,工厂有两种方案对污水进行处理.
方案1:自行处理,达标排放.每处理1立方米所用原料费2元,并且每月排污设备损耗费为30 000元.
方案2:污水纳入污水处理厂统一处理,每处理1立方米污水需付14元的排污费.
问:(1)设工厂每月生产x件产品,每月的利润分别为y1元,y2元,分别求出y1,y2与x的函数关系式.
(2)工厂每月生产多少件产品时,采用两种方案所获利润相同?请说明理由.
(3)工厂每月生产6000件产品时,你采用何种方案才能使工厂所获利润最大?请通过计算加以说明.
22.(12分)某公司销售甲、乙、丙三种型号的器材.3月份公司需支付的工资y1(万元)及其余开支y2(万元)与总销售量x(台)的关系如图9所示.
(1)求y1与x的函数关系式;
(2)若3月份该公司需支付的工资和其余开支共3.8万元,求出这个月三种器材的总销售量;
(3)在(2)的条件下,若3月份公司按2∶3∶1购进甲、乙、丙三种器材,并保证全部卖出.这三种器材的进价和售价如下表所示,求:3月份的总销售利润为多少万元?(总销售利润=销售总价-总进价-需支付的工资-其余开支)
型号 甲 乙 丙
进价(万元/台) 0.9 1.2 1.1
售价(万元/台) 1.2 1.6 1.3
图9
附加题(共20分,不计入总分)
1.(6分)如图1,直线y=x+8与x轴、y轴分别交于点A,B,∠BAO的平分线与y轴交于点M,则OM的长为 .
2.(14分)如图2,已知直线l1:y=kx+b与直线l2:y=x交于点M,直线l1与两坐标轴分别交于A,C两点,且点A的坐标为(0,7),点C的坐标为(7,0).
(1)求直线l1的函数表达式;
(2)在直线l2上是否存在点D,使△ADM的面积等于△AOM面积的2倍,若存在,请求出点D的坐标;若不存在,请说明理由.
图2 备用图
(四川 钟志能)
第四章 一次函数综合测评
一、1.D 2.C 3.C 4. D 5.A 6.C 7.D 8.C 9.B
10.A 提示:由图象可知:甲的速度为60÷3=20(km/h).乙追上甲时,甲走了30 km,此时甲所用的时间为30÷20=1.5(h),乙所用的时间为1.5-1=0.5(h).所以乙的速度为30÷0.5=60(km/h).
设乙休息半小时再次追上甲时,甲所用的时间为t h,则20t=60(t-1-0.5),解得t=2.25.此时甲距离B地为(3-2.25)×20=15(km).
二、11.2 12.y=-6x-2 13.< 14.y=-2x+1
15.4 提示:观察图象,知普通列车的速度为900÷12=75(千米/时),动车的速度为900÷3-75=225(千米/时),则t=900÷225=4.
16.2n-1 提示:根据题意,得第1个,2个,3个,4个,5个正方形的边长分别为1,2,4,8,16.
因为1=20,2=21,4=22,8=23,16=24,所以依此规律得第n个正方形的边长为2n-1.
三、17.解:(1)设y=kx,根据题意,得2k=4,解得k=2.
所以y与x的函数关系式为y=2x.
(2)把x=代入y=2x,得y=-1.
18.解:(1)离家的时间
(2)14 300
(3)1200+(1200-600)+(1500-600)=2700(米).
所以小峰本次去图书馆一共骑行了2700米.
19.解:(1)当x=0时,y=-6;当y=0时,2x-6=0,解得x=3.
所以一次函数y=2x-6与两坐标轴的交点坐标分别为(0,-6),(3,0).
作出函数图象如图所示:
(2)因为当x=4时,y=8-6=2≠3,所以点(4,3)不在该函数的图象上.
(3)由图可知,当x<3时,y<0.
20.解:(1)设直线AB的函数表达式为y=kx+b,根据题意,得6k+b=0,b=2,解得k=.
所以直线AB的函数表达式为.
(2)设点C(x,y).
因为点B(0,2),所以OB=2.
,解得x=±3.
当x=3时,;当x=-3时,.
所以点C的坐标为(-3,3)或(3,1).
21.解:(1)y1=50x-25x-0.5x×2-30000=24x-30 000(x≥0).
y2=50x-25x-0.5x×14=18x(x≥0).
工厂生产5000件产品时,采用两种方案所获利润相同.
理由:当24x-30 000=18x时,解得x=5000.
所以工厂生产5000件产品时,采用两种方案所获利润相同.
(3)当x=6000时,y1=24×6000-30 000=114 000;
y2=18×6000=108 000.
因为y1>y2,所以工厂采用方案1时利润更大.
22.解:(1)设y1与x的函数关系式为y1=kx+b,根据题意,得b=0.2,20k+b=1.2,解得k=0.05.
所以y1与x的函数关系式为y1=0.05x+0.2.
(2)根据题意,得y1+y2=0.05x+0.2+0.005x+0.3=3.8,解得x=60.
所以三月份该公司的总销售量为60台.
(3)3月份售出甲、乙、丙三种型号的器材分别为(台),(台),(台).
(1.2-0.9)×20+(1.6-1.2)×30+(1.3-1.1)×10-3.8=16.2(万元).
所以3月份的总销售利润为16.2万元.
附加题
1.3 提示:如图1,过点M作MN⊥AB于点N.可求得A(6,0),B(0,8).由勾股定理可求得AB=10.因为AM平分∠OAB,所以MO=MN.因为S△OMA+S△BMA=S△OAB,所以×6 OM+×10 MN=×6×8,即8OM=24,解得OM=3.
2.解:(1)因为直线y=kx+b与两坐标轴分别交于A(0,7),C(7,0),所以b=7,7k+b=0,解得k=-1.
所以直线l1的函数表达式为y=-x+7.
(2)因为点M 是直线l1与l2的交点,所以 ,解得x=3.
当x=3时,y=-3+7=4,所以M(3,4).
如图2,过点M作ME⊥x轴于点E,则OE=3,ME=4.
根据勾股定理,得OM=5.
设D(n,n).
①当点D在射线OM上时,因为S△ADM=2S△AOM,且边OM和DM上的高相同,所以DM=2OM=10.所以 OD=15.
所以n2+(n)2=152, 所以n=9或n=-9.
因为点D在第一象限内, 所以n=9,n=12.
所以D(9,12).
②当点D在射线MO上时,因为S△ADM=2S△AOM,且边OM和DM上高相同,所以DM=2OM.所以OM=OD=5.
所以n2+(n)2=52,所以n=3或n=-3.
因为点D在第三象限内,所以n=-3,n=-4.
所以D(-3,-4).
综上,点D的坐标为(9,12)或(-3,-4).
PAGE
第 1 页 共 4 页
第四章 一次函数综合测评
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列函数中是一次函数的是( )
A. B. C. D.
2.直线y=x 4与y轴的交点坐标是( )
A.(-4,0) B.(4,0) C.(0,-4) D.(0,4)
3.下列表示y与x之间关系的图象中,y不是x的函数的是( )
A B C D
4.为了体现尊老、爱老的中华传统美德,重阳节当天学校组织若干名离、退休老教师去“开原市白鹭洲景区”旅游,已知共有y人参加此次重阳节旅游活动,若学校租37座的客车x辆,剩余8人无座位,则y与x之间的关系式为( )
A.y=8x+37 B.y=x+45 C.y=37x-8 D.y=37x+8
5.若ab<0且a>b,则函数y=ax+b的图象大致是( )
A B C D
6.用描点法画一次函数的图象,在如下表格中有一组数据错误,这组错误的数据是( )
A.(-2,12) B.(-1,11) C.(1,10) D.(2,8)
x -2 -1 1 2
y 12 11 10 8
7.根据图1所示的程序计算函数y的值,若输入的x的值是-3和4时,输出的y值相等,则m等于( )
A.-17 B.-25 C.25 D.-43
图1 图2
8.数形结合是解决数学问题常用的思想方法.如图2,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,关于x的方程x+5=ax+b的解是( )
A.x=5 B.x=15 C.x=20 D.x=25
9.关于一次函数y=-2x+b(b为非负数),下列说法:① y随x的增大而减小;②图象一定过第一、二、四象限;③与直线y=1-2x平行.
其中正确的有( )
A.仅① B.仅①③ C.仅②③ D.①②③
10.(2021年衢州)已知A,B两地相距60 km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3 h到达,乙骑摩托车,比甲晚1 h出发,行至30 km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶的时间x的函数关系图象如图3所示.当乙再次追上甲时距离B地( )
A.15 km B.16 km C.44 km D.45 km
图3
二、填空题(本大题共6小题,每小题3分,共18分)
11.已知函数y=(m+2)x|m|-1-3是y关于x的一次函数,则m= .
12.(2021年天津)将直线y=-6x向下平移2个单位长度,平移后直线的表达式为 .
13.已知点A(3,y1)和点B(-2,y2)是一次函数y=-2x+3图象上的两点,则y1与y2的大小关系是y1 y2.(填“>”“=”或“<”)
14.已知y+1与x﹣1成正比例,且当x=3时,y=-5,则y与x的函数关系式是 .
15.某一列动车从A地匀速开往B地,一列普通列车从B地匀速开往A地,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图4中的折线表示y与x之间的函数关系.根据图象进行探究,图中t的值是 .
图4 图5
16.如图5,直线y=x+1与y轴相交于点A1,以OA1为边作正方形OA1B1C1,记作第一个正方形;然后延长C1B1与直线y=x+1相交于点A2,再以C1A2为边作正方形C1A2B2C2,记作第二个正方形;同样延长C2B2与直线y=x+1相交于点A3,再以C2A3为边作正方形C2A3B3C3,记作第三个正方形……依此类推,则第n个正方形的边长为 .
解答题(本大题共6小题,共52分)
17.(6分)已知y与x成正比例,且当x=2时,y=4.
(1)求y与x的函数关系式;
(2)当x=时,求y的值.
18.(8分)周末,小峰骑单车到图书馆,他骑行一段时间后,发现钥匙没在,于是原路返回.在等红绿灯的路口处找到了钥匙,便继续前往图书馆.小峰离家的距离与离家时间的关系如图6所示,请根据图中提供的信息回答下列问题:
(1)图中的自变量是 ;
(2)小峰本次去图书馆一共用了 分钟,在骑行过程中最快的速度是 米/分;
(3)求:小峰本次去图书馆一共骑行了多少米?
图6
19.(8分)已知一次函数y=2x-6,
(1)在图7中画出该函数的图象;
(2)判断(4,3)是否在此函数的图象上;
(3)观察画出的图象,说一说当x为何值时y<0?
图7
20.(8分)如图8,已知点A(6,0),点B(0,2).
(1)求直线AB的函数表达式;
(2)若C为直线AB上一动点,当△OBC的面积为3时,试求点C的坐标.
图8
21.(10分)某工厂生产某种产品,每件产品的成本价为25元,出厂价为50元.在生产过程中,每件产品产生0.5立方米污水,工厂有两种方案对污水进行处理.
方案1:自行处理,达标排放.每处理1立方米所用原料费2元,并且每月排污设备损耗费为30 000元.
方案2:污水纳入污水处理厂统一处理,每处理1立方米污水需付14元的排污费.
问:(1)设工厂每月生产x件产品,每月的利润分别为y1元,y2元,分别求出y1,y2与x的函数关系式.
(2)工厂每月生产多少件产品时,采用两种方案所获利润相同?请说明理由.
(3)工厂每月生产6000件产品时,你采用何种方案才能使工厂所获利润最大?请通过计算加以说明.
22.(12分)某公司销售甲、乙、丙三种型号的器材.3月份公司需支付的工资y1(万元)及其余开支y2(万元)与总销售量x(台)的关系如图9所示.
(1)求y1与x的函数关系式;
(2)若3月份该公司需支付的工资和其余开支共3.8万元,求出这个月三种器材的总销售量;
(3)在(2)的条件下,若3月份公司按2∶3∶1购进甲、乙、丙三种器材,并保证全部卖出.这三种器材的进价和售价如下表所示,求:3月份的总销售利润为多少万元?(总销售利润=销售总价-总进价-需支付的工资-其余开支)
型号 甲 乙 丙
进价(万元/台) 0.9 1.2 1.1
售价(万元/台) 1.2 1.6 1.3
图9
附加题(共20分,不计入总分)
1.(6分)如图1,直线y=x+8与x轴、y轴分别交于点A,B,∠BAO的平分线与y轴交于点M,则OM的长为 .
2.(14分)如图2,已知直线l1:y=kx+b与直线l2:y=x交于点M,直线l1与两坐标轴分别交于A,C两点,且点A的坐标为(0,7),点C的坐标为(7,0).
(1)求直线l1的函数表达式;
(2)在直线l2上是否存在点D,使△ADM的面积等于△AOM面积的2倍,若存在,请求出点D的坐标;若不存在,请说明理由.
图2 备用图
(四川 钟志能)
第四章 一次函数综合测评
一、1.D 2.C 3.C 4. D 5.A 6.C 7.D 8.C 9.B
10.A 提示:由图象可知:甲的速度为60÷3=20(km/h).乙追上甲时,甲走了30 km,此时甲所用的时间为30÷20=1.5(h),乙所用的时间为1.5-1=0.5(h).所以乙的速度为30÷0.5=60(km/h).
设乙休息半小时再次追上甲时,甲所用的时间为t h,则20t=60(t-1-0.5),解得t=2.25.此时甲距离B地为(3-2.25)×20=15(km).
二、11.2 12.y=-6x-2 13.< 14.y=-2x+1
15.4 提示:观察图象,知普通列车的速度为900÷12=75(千米/时),动车的速度为900÷3-75=225(千米/时),则t=900÷225=4.
16.2n-1 提示:根据题意,得第1个,2个,3个,4个,5个正方形的边长分别为1,2,4,8,16.
因为1=20,2=21,4=22,8=23,16=24,所以依此规律得第n个正方形的边长为2n-1.
三、17.解:(1)设y=kx,根据题意,得2k=4,解得k=2.
所以y与x的函数关系式为y=2x.
(2)把x=代入y=2x,得y=-1.
18.解:(1)离家的时间
(2)14 300
(3)1200+(1200-600)+(1500-600)=2700(米).
所以小峰本次去图书馆一共骑行了2700米.
19.解:(1)当x=0时,y=-6;当y=0时,2x-6=0,解得x=3.
所以一次函数y=2x-6与两坐标轴的交点坐标分别为(0,-6),(3,0).
作出函数图象如图所示:
(2)因为当x=4时,y=8-6=2≠3,所以点(4,3)不在该函数的图象上.
(3)由图可知,当x<3时,y<0.
20.解:(1)设直线AB的函数表达式为y=kx+b,根据题意,得6k+b=0,b=2,解得k=.
所以直线AB的函数表达式为.
(2)设点C(x,y).
因为点B(0,2),所以OB=2.
,解得x=±3.
当x=3时,;当x=-3时,.
所以点C的坐标为(-3,3)或(3,1).
21.解:(1)y1=50x-25x-0.5x×2-30000=24x-30 000(x≥0).
y2=50x-25x-0.5x×14=18x(x≥0).
工厂生产5000件产品时,采用两种方案所获利润相同.
理由:当24x-30 000=18x时,解得x=5000.
所以工厂生产5000件产品时,采用两种方案所获利润相同.
(3)当x=6000时,y1=24×6000-30 000=114 000;
y2=18×6000=108 000.
因为y1>y2,所以工厂采用方案1时利润更大.
22.解:(1)设y1与x的函数关系式为y1=kx+b,根据题意,得b=0.2,20k+b=1.2,解得k=0.05.
所以y1与x的函数关系式为y1=0.05x+0.2.
(2)根据题意,得y1+y2=0.05x+0.2+0.005x+0.3=3.8,解得x=60.
所以三月份该公司的总销售量为60台.
(3)3月份售出甲、乙、丙三种型号的器材分别为(台),(台),(台).
(1.2-0.9)×20+(1.6-1.2)×30+(1.3-1.1)×10-3.8=16.2(万元).
所以3月份的总销售利润为16.2万元.
附加题
1.3 提示:如图1,过点M作MN⊥AB于点N.可求得A(6,0),B(0,8).由勾股定理可求得AB=10.因为AM平分∠OAB,所以MO=MN.因为S△OMA+S△BMA=S△OAB,所以×6 OM+×10 MN=×6×8,即8OM=24,解得OM=3.
2.解:(1)因为直线y=kx+b与两坐标轴分别交于A(0,7),C(7,0),所以b=7,7k+b=0,解得k=-1.
所以直线l1的函数表达式为y=-x+7.
(2)因为点M 是直线l1与l2的交点,所以 ,解得x=3.
当x=3时,y=-3+7=4,所以M(3,4).
如图2,过点M作ME⊥x轴于点E,则OE=3,ME=4.
根据勾股定理,得OM=5.
设D(n,n).
①当点D在射线OM上时,因为S△ADM=2S△AOM,且边OM和DM上的高相同,所以DM=2OM=10.所以 OD=15.
所以n2+(n)2=152, 所以n=9或n=-9.
因为点D在第一象限内, 所以n=9,n=12.
所以D(9,12).
②当点D在射线MO上时,因为S△ADM=2S△AOM,且边OM和DM上高相同,所以DM=2OM.所以OM=OD=5.
所以n2+(n)2=52,所以n=3或n=-3.
因为点D在第三象限内,所以n=-3,n=-4.
所以D(-3,-4).
综上,点D的坐标为(9,12)或(-3,-4).
PAGE
第 1 页 共 4 页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
