1.1探索勾股定理(1) 课件(共26张PPT)
文档属性
| 名称 | 1.1探索勾股定理(1) 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 647.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
1.1 探索勾股定理
第一章 勾股定理
第1课时 认识勾股定理
1.了解勾股定理的内容,理解并掌握直角三角形三边之间的数量关系.(重点)
2.能够运用勾股定理进行简单的计算.(难点)
学习目标
B
A
C
图甲
A的面积
B的面积
C的面积
4
4
8
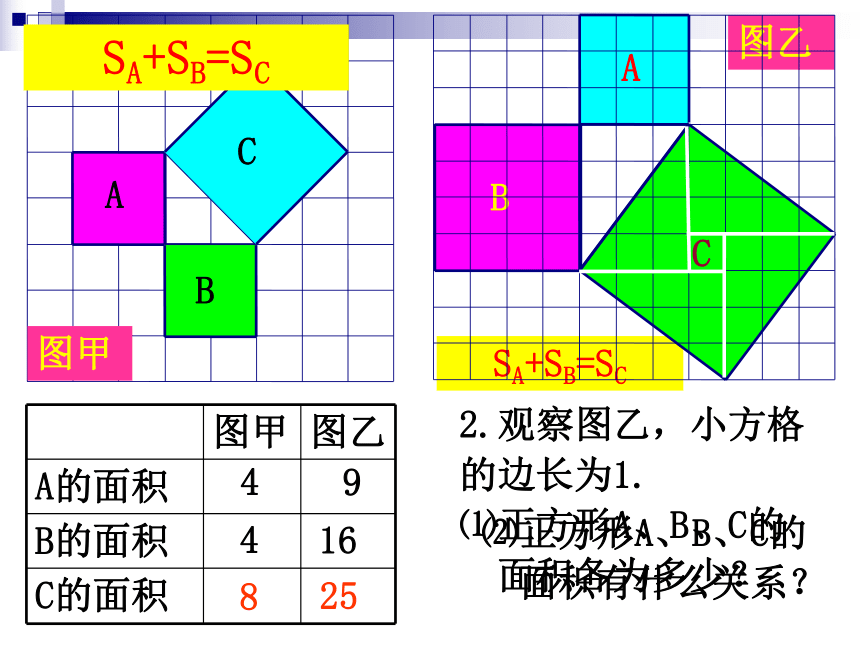
SA+SB=SC
C
图甲
1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
⑵正方形A、B、C的
面积有什么关系?
结论1 以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
二、探索发现勾股定理
A
B
C
图乙
2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
图甲
图甲 图乙
A的面积
B的面积
C的面积
C
SA+SB=SC
A
B
图乙
9
16
25
SA+SB=SC
4
4
8
A
B
C
图甲
图甲 图乙
A的面积
B的面积
C的面积
a
b
c
a
b
c
C
SA+SB=SC
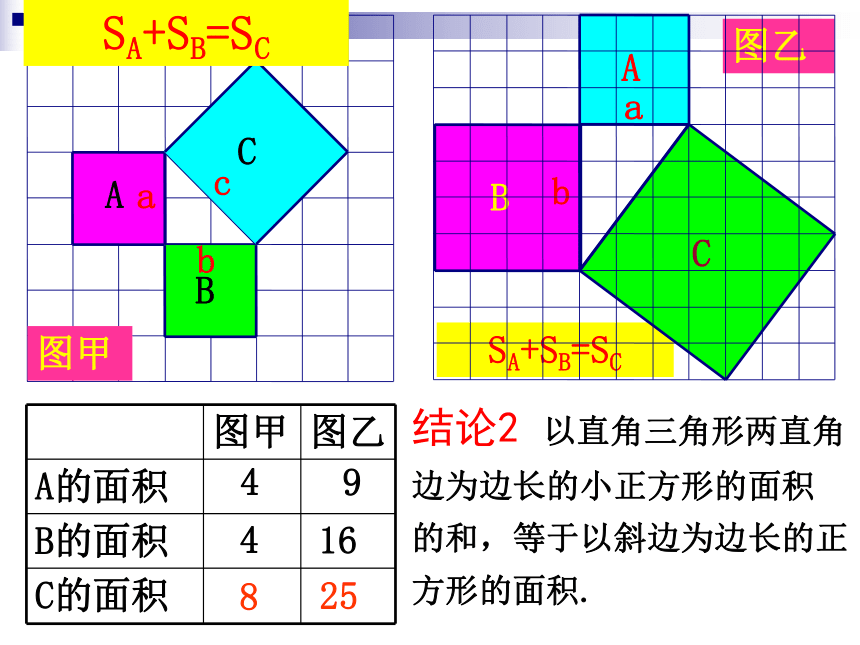
结论2 以直角三角形两直角
边为边长的小正方形的面积
的和,等于以斜边为边长的正
方形的面积.
A
B
C
C
图乙
SA+SB=SC
SA+SB=SC
图甲
a
b
c
a
b
c
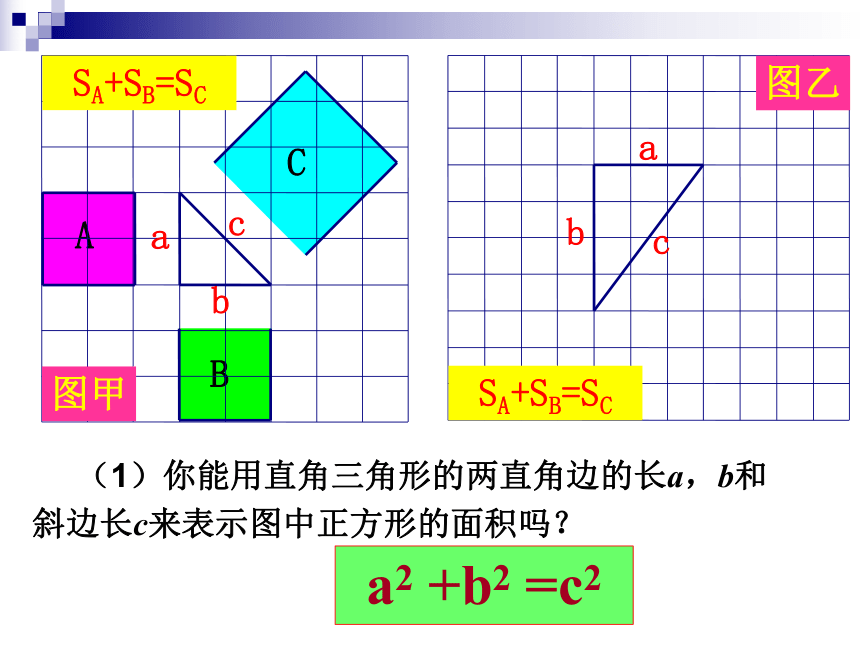
a2 +b2 =c2
(1)你能用直角三角形的两直角边的长a,b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
(3)分别以3厘米、4厘米为直角边作出一个直角三角形,并测量斜边的长度. (2)中的规律对这个三角形仍然成立吗?
小结:
a
b
c
直角三角形两直角边的平方和等于斜边的平方。
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦,“勾股定理”因此而得名. (在西方称为毕达哥拉斯定理)
例题讲解
例1 求下图中字母所代表的正方形的面积。
225
400
A
81
225
B
400
225
400
225
400
225
400
225
400
81
225
400
225
81
225
400
B
225
81
225
400
B
225
81
225
400
B
225
81
225
400
B
225
81
225
400
B
225
81
225
A
400
625
144
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
练一练
答案:15 5 7
例2 求出下列直角三角形中未知边的长度
6
8
x
5
x
13
例题讲解
A
B
C
比一比看看谁算得快!
1.求下列直角三角形中未知边的长:
可用勾股定理直接计算.
方法小结:
8
x
17
16
20
x
12
5
x
练一练
已知直角三角形两边长,求第三边长.
变式:在Rt△ABC中,a,b,c分别表示直角边和斜边
1、如果a=6,b:c=4:5,求b,c
2、如果a=5,斜边c比另一直角边b多1,求b和c
答案:1、b=8 ,c=10
2、c=13 ,b=12
2、如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识
求AC、AB、BC的平方
3、如图,三条大路交于点
A、B、C,且∠A =90°,
AB=3 km,AC=4 km,求交汇
点A到大路BC的最近距离是多少?
A
B
C
D
练习:
答案:AC的平方为65,AB的平方为13
BC的平方为52
答案:2.8
三、简单应用
例 3 如图所示,一棵大树在一次强烈台风中于离地面10 m处折断倒下,树顶落在离树根24 m处. 大树在折断之前高多少米?
解:∵△ABC是直角三角形,AB=10 m,AC=24 m,
由勾股定理得
即
∴大树的高度=AB+BC=10+26=36(m).
例4 已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
、利用勾股定理进行计算
四
典例精析
解:由勾股定理可得,
AB2=AC2+BC2=25,
即 AB=5.
根据三角形面积公式,
得 AC×BC= AB×CD.
∴ CD= .
A
D
B
C
3
4
25或 7
1、已知:Rt△ABC中,AB=4,AC=3,则BC的平方为___________ .
4
3
A
C
B
4
3
C
A
B
提高训练
2.在Rt△ABC中,∠C=90°,已知AB=2,求
答案:8
A
B
C
D
7cm
3、如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
提高训练
4、如图,一块直角三角形的纸片,两直
角边AC=6㎝,BC=8㎝。现将直角边AC
沿直线AD折叠,使它落在斜边AB上,
且与AE重合,则CD等于多少?
解:由折叠的性质知CD=DE,
AC=AE.
根据题意在Rt△BDE中运用勾股定理求DE.
由勾股定理得,AB=10.
由折叠的性质知,AE=AC=6,
DE=CD,∠AED=∠C=90°.
∴BE=AB-AE=10-6=4.
在Rt△BDE中,由勾股定理得,
即
,解得CD=3cm.
5、如图,在△ABC中,AB=15㎝,
AC=13㎝,BC=14㎝,求△ABC的面积
D
解:当高AD在△ABC内部时,如图①.
在Rt△ABD中,由勾股定理,
得BD2=AB2-AD2=202-122=162,
∴BD=16;
在Rt△ACD中,由勾股定理,
得CD2=AC2-AD2=152-122=81,
∴CD=9.
∴BC=BD+CD=25.
∴△ABC的周长为25+20+15=60.
6. 在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,求△ABC的周长.
思维拓展
题中未给出图形,作高构造直角三角形时,易漏掉钝角三角形的情况.如在本例题中,易只考虑高AD在△ABC内的情形,忽视高AD在△ABC外的情形.
当高AD在△ABC外部时,如图②.
同理可得 BD=16,CD=9.
∴BC=BD-CD=7.
∴△ABC的周长为7+20+15=42.
综上所述,△ABC的周长为42或60.
方法总结
解析:因为AE=BE,
所以S△ABE= AE·BE= AE2.
又因为AE2+BE2=AB2,
所以2AE2=AB2,
所以S△ABE= AB2= ;
同理可得S△AHC+S△BCF= AC2+ BC2.
又因为AC2+BC2=AB2,
所以阴影部分的面积为 AB2= .
7. 如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中△ABE的面积为________,阴影部分的面积为________.
a
b
c
即:直角三角形两直角边的平方和等于斜边的平方。
如果直角三角形两直角边分别为a、b,斜边为c,那么
勾股定理
1.1 探索勾股定理
第一章 勾股定理
第1课时 认识勾股定理
1.了解勾股定理的内容,理解并掌握直角三角形三边之间的数量关系.(重点)
2.能够运用勾股定理进行简单的计算.(难点)
学习目标
B
A
C
图甲
A的面积
B的面积
C的面积
4
4
8
SA+SB=SC
C
图甲
1.观察图甲,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
⑵正方形A、B、C的
面积有什么关系?
结论1 以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
二、探索发现勾股定理
A
B
C
图乙
2.观察图乙,小方格
的边长为1.
⑴正方形A、B、C的
面积各为多少?
9
16
25
SA+SB=SC
⑵正方形A、B、C的
面积有什么关系?
4
4
8
A
B
C
图甲
图甲 图乙
A的面积
B的面积
C的面积
C
SA+SB=SC
A
B
图乙
9
16
25
SA+SB=SC
4
4
8
A
B
C
图甲
图甲 图乙
A的面积
B的面积
C的面积
a
b
c
a
b
c
C
SA+SB=SC
结论2 以直角三角形两直角
边为边长的小正方形的面积
的和,等于以斜边为边长的正
方形的面积.
A
B
C
C
图乙
SA+SB=SC
SA+SB=SC
图甲
a
b
c
a
b
c
a2 +b2 =c2
(1)你能用直角三角形的两直角边的长a,b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
(3)分别以3厘米、4厘米为直角边作出一个直角三角形,并测量斜边的长度. (2)中的规律对这个三角形仍然成立吗?
小结:
a
b
c
直角三角形两直角边的平方和等于斜边的平方。
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦,“勾股定理”因此而得名. (在西方称为毕达哥拉斯定理)
例题讲解
例1 求下图中字母所代表的正方形的面积。
225
400
A
81
225
B
400
225
400
225
400
225
400
225
400
81
225
400
225
81
225
400
B
225
81
225
400
B
225
81
225
400
B
225
81
225
400
B
225
81
225
400
B
225
81
225
A
400
625
144
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
练一练
答案:15 5 7
例2 求出下列直角三角形中未知边的长度
6
8
x
5
x
13
例题讲解
A
B
C
比一比看看谁算得快!
1.求下列直角三角形中未知边的长:
可用勾股定理直接计算.
方法小结:
8
x
17
16
20
x
12
5
x
练一练
已知直角三角形两边长,求第三边长.
变式:在Rt△ABC中,a,b,c分别表示直角边和斜边
1、如果a=6,b:c=4:5,求b,c
2、如果a=5,斜边c比另一直角边b多1,求b和c
答案:1、b=8 ,c=10
2、c=13 ,b=12
2、如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识
求AC、AB、BC的平方
3、如图,三条大路交于点
A、B、C,且∠A =90°,
AB=3 km,AC=4 km,求交汇
点A到大路BC的最近距离是多少?
A
B
C
D
练习:
答案:AC的平方为65,AB的平方为13
BC的平方为52
答案:2.8
三、简单应用
例 3 如图所示,一棵大树在一次强烈台风中于离地面10 m处折断倒下,树顶落在离树根24 m处. 大树在折断之前高多少米?
解:∵△ABC是直角三角形,AB=10 m,AC=24 m,
由勾股定理得
即
∴大树的高度=AB+BC=10+26=36(m).
例4 已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
、利用勾股定理进行计算
四
典例精析
解:由勾股定理可得,
AB2=AC2+BC2=25,
即 AB=5.
根据三角形面积公式,
得 AC×BC= AB×CD.
∴ CD= .
A
D
B
C
3
4
25或 7
1、已知:Rt△ABC中,AB=4,AC=3,则BC的平方为___________ .
4
3
A
C
B
4
3
C
A
B
提高训练
2.在Rt△ABC中,∠C=90°,已知AB=2,求
答案:8
A
B
C
D
7cm
3、如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
提高训练
4、如图,一块直角三角形的纸片,两直
角边AC=6㎝,BC=8㎝。现将直角边AC
沿直线AD折叠,使它落在斜边AB上,
且与AE重合,则CD等于多少?
解:由折叠的性质知CD=DE,
AC=AE.
根据题意在Rt△BDE中运用勾股定理求DE.
由勾股定理得,AB=10.
由折叠的性质知,AE=AC=6,
DE=CD,∠AED=∠C=90°.
∴BE=AB-AE=10-6=4.
在Rt△BDE中,由勾股定理得,
即
,解得CD=3cm.
5、如图,在△ABC中,AB=15㎝,
AC=13㎝,BC=14㎝,求△ABC的面积
D
解:当高AD在△ABC内部时,如图①.
在Rt△ABD中,由勾股定理,
得BD2=AB2-AD2=202-122=162,
∴BD=16;
在Rt△ACD中,由勾股定理,
得CD2=AC2-AD2=152-122=81,
∴CD=9.
∴BC=BD+CD=25.
∴△ABC的周长为25+20+15=60.
6. 在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,求△ABC的周长.
思维拓展
题中未给出图形,作高构造直角三角形时,易漏掉钝角三角形的情况.如在本例题中,易只考虑高AD在△ABC内的情形,忽视高AD在△ABC外的情形.
当高AD在△ABC外部时,如图②.
同理可得 BD=16,CD=9.
∴BC=BD-CD=7.
∴△ABC的周长为7+20+15=42.
综上所述,△ABC的周长为42或60.
方法总结
解析:因为AE=BE,
所以S△ABE= AE·BE= AE2.
又因为AE2+BE2=AB2,
所以2AE2=AB2,
所以S△ABE= AB2= ;
同理可得S△AHC+S△BCF= AC2+ BC2.
又因为AC2+BC2=AB2,
所以阴影部分的面积为 AB2= .
7. 如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中△ABE的面积为________,阴影部分的面积为________.
a
b
c
即:直角三角形两直角边的平方和等于斜边的平方。
如果直角三角形两直角边分别为a、b,斜边为c,那么
勾股定理
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
