1.1探索勾股定理(2) 课件(共19张PPT)
文档属性
| 名称 | 1.1探索勾股定理(2) 课件(共19张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 642.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
回味获新知
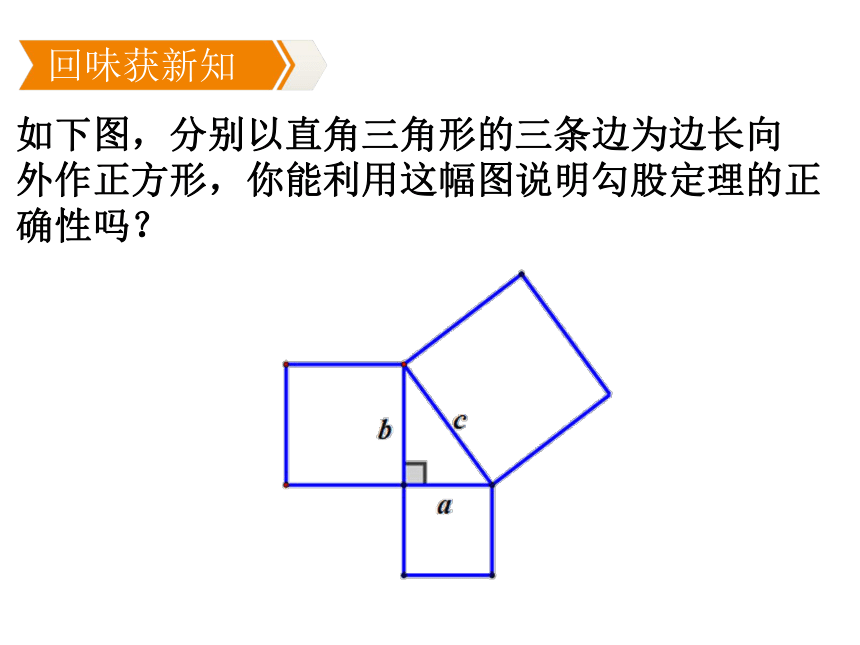
如下图,分别以直角三角形的三条边为边长向
外作正方形,你能利用这幅图说明勾股定理的正
确性吗?
1.1 探索勾股定理
第一章 勾股定理
第2课时 验证勾股定理
学习目标
1.学会用几种方法验证勾股定理.(重点)
2.能够运用勾股定理解决简单问题.(重点,难点)
a+b
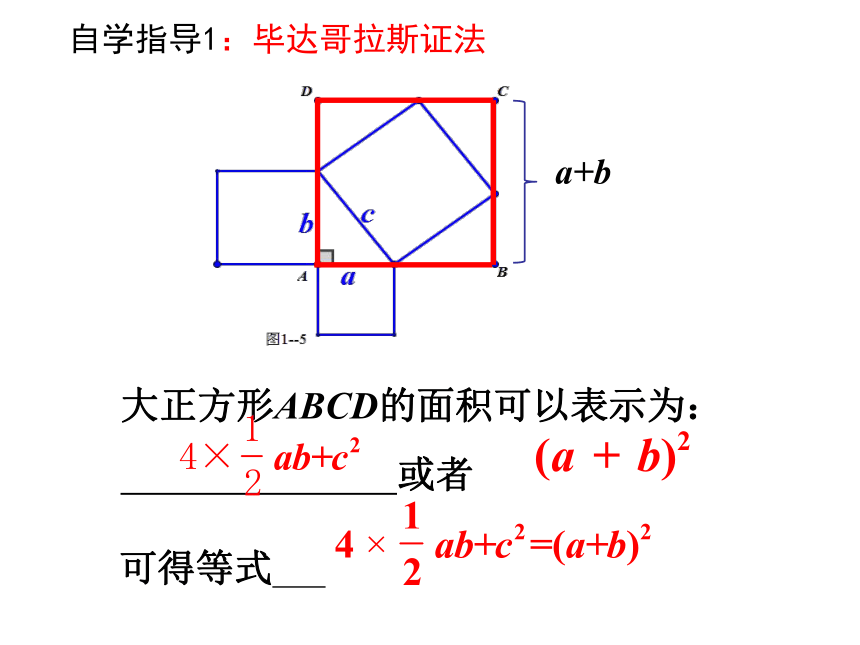
大正方形ABCD的面积可以表示为:
或者
可得等式
自学指导1:毕达哥拉斯证法
A
B
C
D
小正方形ABCD的面积可以表示为: 或者
可得等式
自学指导1赵爽弦图
做8个全等的直角三角形,设它们的两条直角边长分别为
a,b,斜边长为c,再做三个边长分别为a、b、c的正方形,
把它们像上图那样拼成两个正方形,利用这两个正方形的
面积也可证明勾股定理
拼图法
从图上可以看到,这两个正方形的边长都是a+b,所以面积相等即
整理得
a
b
c
a
b
c
=
=
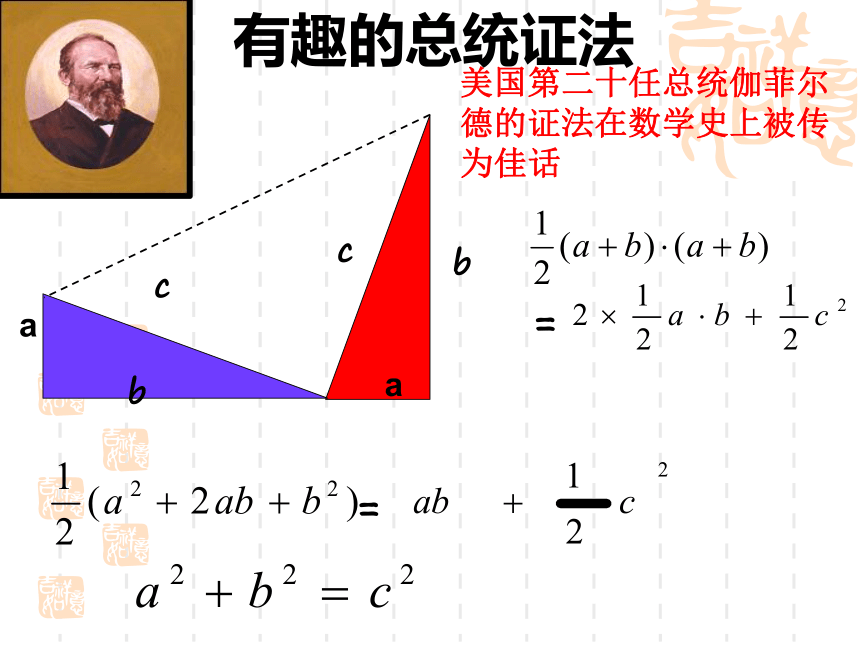
有趣的总统证法
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话
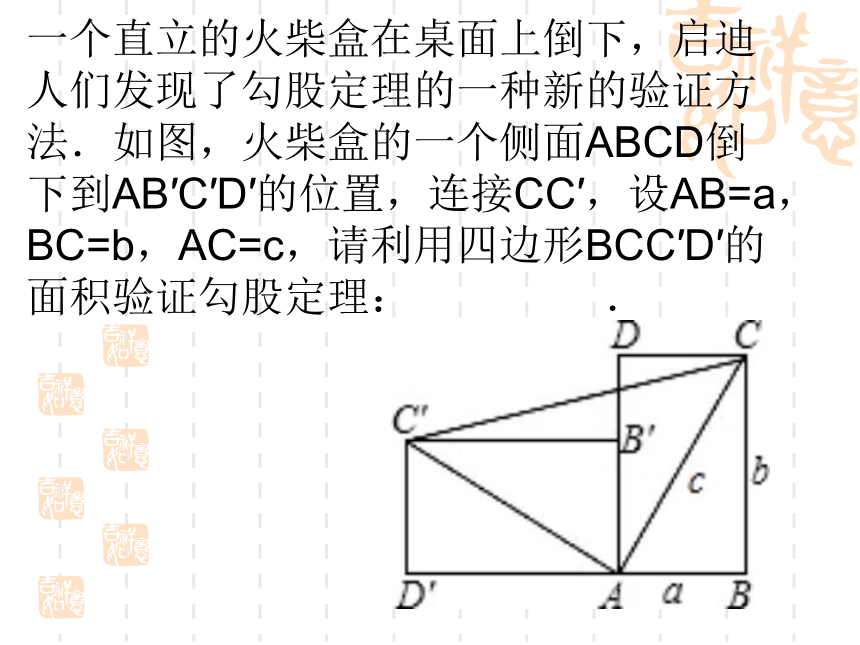
一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积验证勾股定理: .
议一议
a
b
c
b
a
c
(1)
(2)
观察右图,用数格子的方法判断图中三角形的三边长是否满足 a +b =c .
钝角三角形和锐角三角形的三边长都不满足 a +b =c .
例1、如图是某处公路的示意图,AB=1500米,AC=900米,AC ⊥BC,如果一辆农用车以18千米/时的速度行驶,那么它从A直接到B 与从A经过C到B相比较,可以节约多少时间?
A
B
C
练习1.一架飞机在天空中水平飞行,某一时刻正好飞到一个男孩头顶正上方3000米处,过了20秒,飞机距离这个男孩头顶5000米,试求这架飞机的飞行速度
20秒
3000米
5000米
A
B
C
练习2 如图所示,校园内有两棵树相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 米.
13米
12米
8米
A
B
C
13
3.如图,某储藏室入口的截面是一个半径为1.2米的半圆形,一个长、宽高分别是1.2米,1米,0.8米的箱子能放进储藏室吗?
书本 P7 T3
4.如图,已知长方形ABCD中,AB=8 cm,BC=10 cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.
5. 如图,高速公路的同侧有A,B两个村庄,它们到高速公路所在直线MN的距离分别为AA1=2km,BB1=4km,A1B1=8km.现要在高速公路上A1、B1之间设一个出口P,使A,B两个村庄到P的距离之和最短,求这个最短距离和.
自学检测
解:作点B关于MN的对称
点B′,连接AB′,交A1B1于
P点,连BP.
则AP+BP=AP+PB′=AB′,
易知P点即为到点A,B距离之和最短的点.
过点A作AE⊥BB′于点E,
则AE=A1B1=8km,B′E=AA1+BB1=2+4=6(km).
由勾股定理,得B′A2=AE2+B′E2=82+62=100.
∴AB′=10(km).即AP+BP=AB′=10km.
故出口P到A,B两村庄的最短距离和是10km.
变式:如图,在一条公路上有A、B两站相距25km,C、D为两个小镇,已知DA⊥AB,CB ⊥AB, DA=15km,CB= 10km,现在要在公路边上建设一个加油站E,使得它到两镇的距离相等,请问E站应建在距A站多远处
D
A
E
B
C
15
10
25-x
7.如图,直线l上有三个正方形a、b、c,若a、c的面积分别为5和11,则b的面积为( )
A.7 B.11 C.16 D.18
A
B
C
A的面积+B的面积=C的面积
D
A
B
C
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.
⒉勾股定理: 直角三角形两直角边a、b的平方和,等于斜边c平方
a2+b2 =c2
⒊勾股定理的主要作用是 在直角三角形中,已知任意两边求第三边的长
回味获新知
如下图,分别以直角三角形的三条边为边长向
外作正方形,你能利用这幅图说明勾股定理的正
确性吗?
1.1 探索勾股定理
第一章 勾股定理
第2课时 验证勾股定理
学习目标
1.学会用几种方法验证勾股定理.(重点)
2.能够运用勾股定理解决简单问题.(重点,难点)
a+b
大正方形ABCD的面积可以表示为:
或者
可得等式
自学指导1:毕达哥拉斯证法
A
B
C
D
小正方形ABCD的面积可以表示为: 或者
可得等式
自学指导1赵爽弦图
做8个全等的直角三角形,设它们的两条直角边长分别为
a,b,斜边长为c,再做三个边长分别为a、b、c的正方形,
把它们像上图那样拼成两个正方形,利用这两个正方形的
面积也可证明勾股定理
拼图法
从图上可以看到,这两个正方形的边长都是a+b,所以面积相等即
整理得
a
b
c
a
b
c
=
=
有趣的总统证法
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话
一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积验证勾股定理: .
议一议
a
b
c
b
a
c
(1)
(2)
观察右图,用数格子的方法判断图中三角形的三边长是否满足 a +b =c .
钝角三角形和锐角三角形的三边长都不满足 a +b =c .
例1、如图是某处公路的示意图,AB=1500米,AC=900米,AC ⊥BC,如果一辆农用车以18千米/时的速度行驶,那么它从A直接到B 与从A经过C到B相比较,可以节约多少时间?
A
B
C
练习1.一架飞机在天空中水平飞行,某一时刻正好飞到一个男孩头顶正上方3000米处,过了20秒,飞机距离这个男孩头顶5000米,试求这架飞机的飞行速度
20秒
3000米
5000米
A
B
C
练习2 如图所示,校园内有两棵树相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 米.
13米
12米
8米
A
B
C
13
3.如图,某储藏室入口的截面是一个半径为1.2米的半圆形,一个长、宽高分别是1.2米,1米,0.8米的箱子能放进储藏室吗?
书本 P7 T3
4.如图,已知长方形ABCD中,AB=8 cm,BC=10 cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.
5. 如图,高速公路的同侧有A,B两个村庄,它们到高速公路所在直线MN的距离分别为AA1=2km,BB1=4km,A1B1=8km.现要在高速公路上A1、B1之间设一个出口P,使A,B两个村庄到P的距离之和最短,求这个最短距离和.
自学检测
解:作点B关于MN的对称
点B′,连接AB′,交A1B1于
P点,连BP.
则AP+BP=AP+PB′=AB′,
易知P点即为到点A,B距离之和最短的点.
过点A作AE⊥BB′于点E,
则AE=A1B1=8km,B′E=AA1+BB1=2+4=6(km).
由勾股定理,得B′A2=AE2+B′E2=82+62=100.
∴AB′=10(km).即AP+BP=AB′=10km.
故出口P到A,B两村庄的最短距离和是10km.
变式:如图,在一条公路上有A、B两站相距25km,C、D为两个小镇,已知DA⊥AB,CB ⊥AB, DA=15km,CB= 10km,现在要在公路边上建设一个加油站E,使得它到两镇的距离相等,请问E站应建在距A站多远处
D
A
E
B
C
15
10
25-x
7.如图,直线l上有三个正方形a、b、c,若a、c的面积分别为5和11,则b的面积为( )
A.7 B.11 C.16 D.18
A
B
C
A的面积+B的面积=C的面积
D
A
B
C
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.
⒉勾股定理: 直角三角形两直角边a、b的平方和,等于斜边c平方
a2+b2 =c2
⒊勾股定理的主要作用是 在直角三角形中,已知任意两边求第三边的长
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
