1.2一定是直角三角形吗 课件(共25张PPT)
文档属性
| 名称 | 1.2一定是直角三角形吗 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 394.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 21:20:41 | ||
图片预览








文档简介
(共25张PPT)
如果直角三角形两条直角边长分别为a,b,斜边长为c,那么
a2 + b2 = c2
勾股定理的内容是什么?
回顾旧知
古埃及人曾用下面的方法得到直角三角形:
打13个等距的结,把一根绳子分成等长的12段,然后以3段,4段,5段的长度为边长,用木桩钉成一个三角形,其中一个角便是直角三角形.
32 + 42 = 52
直角三角形
这种方法正确吗?满足这个条件的三角形是直角三角形吗?这就是我们这节课要研究的内容。
1.2 一定是直角三角形吗
第一章 勾股定理
学习目标
1.探索勾股定理的逆定理并熟悉一些常见的勾股数。(重点)
2. 应用勾股定理的逆定理判定一个三角形是否是直角三角形。(难点)
知识讲解一、直角三角形的判定
探究:下面有两组数分别是一个三角形的三边长a, b, c:
①3,4,5; ②6,8,10;
回答下列问题:
1.这两组数都满足 a2+b2=c2吗?
2.分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
知识归纳1
直角三角形的判定(勾股定理的逆定理)
(1)文字语言:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
A
B
C
a
b
c
在△ABC中,a2+b2=c2
(2)符号语言:
∴△ABC为直角三角形
(3)应用:用来判定三角形的形状。
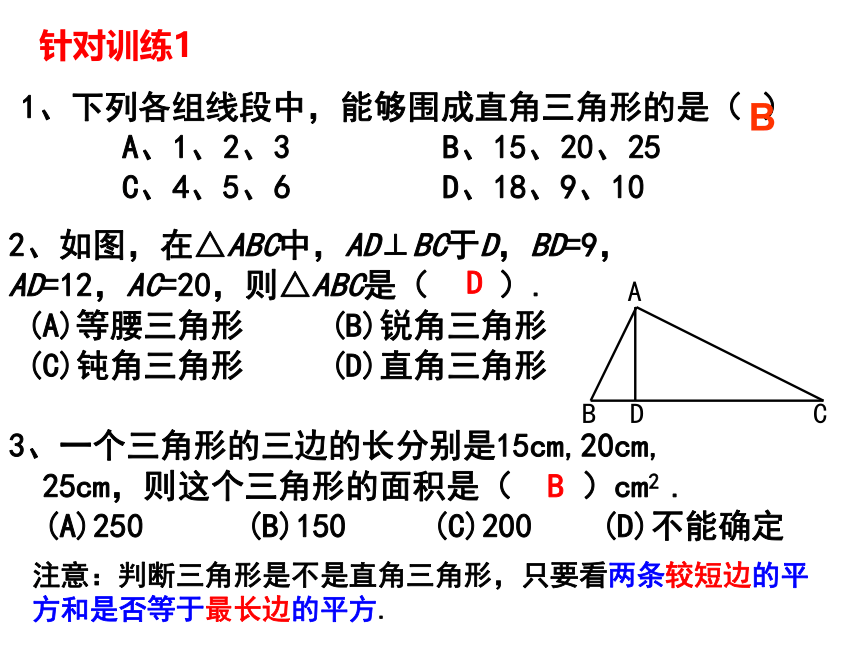
1、下列各组线段中,能够围成直角三角形的是( )
A、1、2、3 B、15、20、25
C、4、5、6 D、18、9、10
B
针对训练1
2、如图,在△ABC中,AD⊥BC于D,BD=9,
AD=12,AC=20,则△ABC是( ).
(A)等腰三角形 (B)锐角三角形
(C)钝角三角形 (D)直角三角形
3、一个三角形的三边的长分别是15cm,20cm,
25cm,则这个三角形的面积是( )cm2 .
(A)250 (B)150 (C)200 (D)不能确定
A
B
D
C
B
D
注意:判断三角形是不是直角三角形,只要看两条较短边的平方和是否等于最长边的平方.
92+122=152
以上两组数有什么特点?
62+82=102
1、都是正整数;
(1) 9,12,15; (2) 6,8,10;
2、都满足a2+b2=c2。
知识讲解二、勾股数
“勾股数”的定义:
满足a2+b2=c2的三个正整数,称为勾股数。
知识归纳2
常见勾股数:
3,4,5; 5,12,13; 6,8,10;
7,24,25; 8,15,17; 9,40,41;
2倍 3倍 3 4 5 6 8 10 9 12 15
5 12 13 10 24 26 15 36 39
8 15 17 16 30 34 24 45 51
7 24 25 14 48 50 21 72 75
4倍 10倍 12 16 20 30 40 50
20 48 52 50 120 130
32 60 68 80 150 170
28 96 100 70 240 250
勾股数扩大n (n为正整数)倍,还是勾股数
三边同时扩大或缩小相同的倍数,三角形形状不变。
1.下列几组数据:是直角三角形的三边的有几组?是勾股数的是哪组?
(1)9,12,15; (2)1.5,3.6,3.9;
(3)12,35,36 ; (4)12,18,22.
2.将直角三角形的三边长同时扩大3.5倍
后,得到的三角形是( ).
(A)直角三角形 (B)锐角三角形
(C)钝角三角形 (D)不能确定
解:直角三角形的三边的有(1)、(2)
勾股数的是(1)
A
易错点:勾股数必须是
正整数。
针对训练2
例1一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图2所示,这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图1
图2
三、直角三角形的判定的简单应用
在△BCD中,
所以△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
所以△ABD 是直角三角形,∠A是直角.
练习:(课本P10随堂练习2)如图,在正方形ABCD中,AB=4,AE=2,DF=1, 图中有几个直角三角形,你是如何判断的?
4
1
2
2
4
3
解:图中共有4个直角三角形,分别为
Rt△ABE,Rt△BCF,Rt△DEF,Rt△BEF.理由:
∵在正方形ABCD中,∠A=∠C=∠D=90°
∴△ABE,△BCF,△DEF都为直角三角形
由勾股定理得:
BE =2 +4 =20,EF =2 +1 =5
BF =3 +4 =25,∴BE +EF =BF
∴△BEF是直角三角形。
点拨:判断一个三角形是否为直角三角形的方法:
(1)根据定义判断(找直角);
(2)根据三边关系判断(直角三角形的判定方法)。
例2 下面以a,b,c为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) a=15 , b=8 ,c=17;
解:因为152+82=289,172=289,所以152+82=172,根据勾股定理的逆定理,这个三角形是直角三角形,且∠C是直角.
(2) a=13 , b=14 , c=15;
解:因为132+142=365,152=225,所以132+142≠152,不符合勾股定理的逆定理,所以这个三角形不是直角三角形.
(3) a:b: c=3:4:5;
解:设a=3k,b=4k,c=5k,
因为(3k)2+(4k)2=25k2,(5k)2=25k2,
所以(3k)2+(4k)2=(5k)2,根据勾股定理的逆定理,这个三角形是直角三角形,∠C是直角.
根据勾股定理及直角三角形的判定方法,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
归纳
变式: 已知△ABC,AB=n -1,BC=2n,AC=n +1(n为
大于1的正整数).试问△ABC是直角三角形吗?若是,
哪一条边所对的角是直角?请说明理由
解:∵AB +BC =(n -1) +(2n)
=n4 -2n +1+4n
=n4 +2n +1,
AC =(n +1) =n4 +2n +1,
∴AB +BC = AC .
∴△ABC直角三角形,边AC所对的角是直角.
先确定AB、BC、AC、
的大小
例3 在正方形ABCD中,F是CD的中点,E为BC上一点,且CE= CB,试判断AF与EF的
位置关系,并说明理由.
解:AF⊥EF.理由:设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
一、直角三角形的判定(勾股定理的逆定理):
文字语言:
如果三角形三边长a,b,c满足a +b =c ,
那么这个三角形是直角三角形
几何语言:
∵ a +b =c
∴ ∠C=90°(c为斜边)
a
b
c
应用:
用来判定三角形的形状。
1. 三个数满足a +b =c ,
2. 三个数都是正整数。
二、勾股数满足的条件是:
知识小结
2.如果线段a,b,c能组成直角三角形, 则它们的比可能是 ( )
A.3:4:7 B.5:12:13 C.1:2:4 D.1:3:5
当堂训练
B
1.已知 ABC中, BC=41, AC=40, AB=9, 则此三角形为_______三角形, ______是最大角.
三角形的三边分别是a,b,c, 且满足等式 (a+b)2-c2=2ab, 则此三角形是 ( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 等腰直角三角形
A
直角
∠A
4、下列各组数是勾股数的是( )
A.6,8,10 B.7,8,9
C.0.3,0.4,0.5 D.52,122,132
A
方法点拨:根据勾股数的定义,勾股数必须为正整数,先排除小数,再计算最长边的平方是否等于其他两边的平方和即可.
5、如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3 cm,BC=4 cm,求△ABC的面积.
解: ∵ S△ACD=30 cm2,DC=12 cm.
∴ AC=5 cm,
又∵
∴△ABC是直角三角形, ∠B是直角.
∴
D
C
B
A
①②④
6.若△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B-∠C;②a2=(b+c)(b-c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:12:13.其中能判定△ABC是直角三角形的是_____________.(填序号)
7.如图,四边形ABCD中,已知AB=3,BC=4,CD=12,DA=13, 且∠ABC=900,求这个四边形的面积.
解:如图,连接AC.
在Rt△ABC中,由勾股定理,
得 AC2=AB2+BC2,∴AC=5,
又∵ CD=12cm,AD=13cm
∴ AD2=CD2+AC2,∴△ACD是直角三角形.
S四边形ABCD=SRt△ABC+SRt△ACD= (3×4+5×12)÷2=36.
变式:如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.
解:如图,连接BD.
在Rt△ABD中,由勾股定理,
得 BD2=AB2+AD2,∴BD=5m,
又∵ CD=12cm,BC=13cm
∴ BC2=CD2+BD2,∴△BDC是直角三角形, ∠CDB是直角.
S四边形ABCD=SRt△BCD-SRt△ABD= BD CD- AB AD
= (5×12-3×4)=24 m2.
C
B
A
D
8、探索勾股数的规律:观察下列各组数:
(3,4,5),(5,12,13),(7,24,25),
(9,40,41)...可发现,
...请写出第五个数组:___________
(11,60,61)
如果直角三角形两条直角边长分别为a,b,斜边长为c,那么
a2 + b2 = c2
勾股定理的内容是什么?
回顾旧知
古埃及人曾用下面的方法得到直角三角形:
打13个等距的结,把一根绳子分成等长的12段,然后以3段,4段,5段的长度为边长,用木桩钉成一个三角形,其中一个角便是直角三角形.
32 + 42 = 52
直角三角形
这种方法正确吗?满足这个条件的三角形是直角三角形吗?这就是我们这节课要研究的内容。
1.2 一定是直角三角形吗
第一章 勾股定理
学习目标
1.探索勾股定理的逆定理并熟悉一些常见的勾股数。(重点)
2. 应用勾股定理的逆定理判定一个三角形是否是直角三角形。(难点)
知识讲解一、直角三角形的判定
探究:下面有两组数分别是一个三角形的三边长a, b, c:
①3,4,5; ②6,8,10;
回答下列问题:
1.这两组数都满足 a2+b2=c2吗?
2.分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
知识归纳1
直角三角形的判定(勾股定理的逆定理)
(1)文字语言:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
A
B
C
a
b
c
在△ABC中,a2+b2=c2
(2)符号语言:
∴△ABC为直角三角形
(3)应用:用来判定三角形的形状。
1、下列各组线段中,能够围成直角三角形的是( )
A、1、2、3 B、15、20、25
C、4、5、6 D、18、9、10
B
针对训练1
2、如图,在△ABC中,AD⊥BC于D,BD=9,
AD=12,AC=20,则△ABC是( ).
(A)等腰三角形 (B)锐角三角形
(C)钝角三角形 (D)直角三角形
3、一个三角形的三边的长分别是15cm,20cm,
25cm,则这个三角形的面积是( )cm2 .
(A)250 (B)150 (C)200 (D)不能确定
A
B
D
C
B
D
注意:判断三角形是不是直角三角形,只要看两条较短边的平方和是否等于最长边的平方.
92+122=152
以上两组数有什么特点?
62+82=102
1、都是正整数;
(1) 9,12,15; (2) 6,8,10;
2、都满足a2+b2=c2。
知识讲解二、勾股数
“勾股数”的定义:
满足a2+b2=c2的三个正整数,称为勾股数。
知识归纳2
常见勾股数:
3,4,5; 5,12,13; 6,8,10;
7,24,25; 8,15,17; 9,40,41;
2倍 3倍 3 4 5 6 8 10 9 12 15
5 12 13 10 24 26 15 36 39
8 15 17 16 30 34 24 45 51
7 24 25 14 48 50 21 72 75
4倍 10倍 12 16 20 30 40 50
20 48 52 50 120 130
32 60 68 80 150 170
28 96 100 70 240 250
勾股数扩大n (n为正整数)倍,还是勾股数
三边同时扩大或缩小相同的倍数,三角形形状不变。
1.下列几组数据:是直角三角形的三边的有几组?是勾股数的是哪组?
(1)9,12,15; (2)1.5,3.6,3.9;
(3)12,35,36 ; (4)12,18,22.
2.将直角三角形的三边长同时扩大3.5倍
后,得到的三角形是( ).
(A)直角三角形 (B)锐角三角形
(C)钝角三角形 (D)不能确定
解:直角三角形的三边的有(1)、(2)
勾股数的是(1)
A
易错点:勾股数必须是
正整数。
针对训练2
例1一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图2所示,这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图1
图2
三、直角三角形的判定的简单应用
在△BCD中,
所以△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
所以△ABD 是直角三角形,∠A是直角.
练习:(课本P10随堂练习2)如图,在正方形ABCD中,AB=4,AE=2,DF=1, 图中有几个直角三角形,你是如何判断的?
4
1
2
2
4
3
解:图中共有4个直角三角形,分别为
Rt△ABE,Rt△BCF,Rt△DEF,Rt△BEF.理由:
∵在正方形ABCD中,∠A=∠C=∠D=90°
∴△ABE,△BCF,△DEF都为直角三角形
由勾股定理得:
BE =2 +4 =20,EF =2 +1 =5
BF =3 +4 =25,∴BE +EF =BF
∴△BEF是直角三角形。
点拨:判断一个三角形是否为直角三角形的方法:
(1)根据定义判断(找直角);
(2)根据三边关系判断(直角三角形的判定方法)。
例2 下面以a,b,c为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) a=15 , b=8 ,c=17;
解:因为152+82=289,172=289,所以152+82=172,根据勾股定理的逆定理,这个三角形是直角三角形,且∠C是直角.
(2) a=13 , b=14 , c=15;
解:因为132+142=365,152=225,所以132+142≠152,不符合勾股定理的逆定理,所以这个三角形不是直角三角形.
(3) a:b: c=3:4:5;
解:设a=3k,b=4k,c=5k,
因为(3k)2+(4k)2=25k2,(5k)2=25k2,
所以(3k)2+(4k)2=(5k)2,根据勾股定理的逆定理,这个三角形是直角三角形,∠C是直角.
根据勾股定理及直角三角形的判定方法,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
归纳
变式: 已知△ABC,AB=n -1,BC=2n,AC=n +1(n为
大于1的正整数).试问△ABC是直角三角形吗?若是,
哪一条边所对的角是直角?请说明理由
解:∵AB +BC =(n -1) +(2n)
=n4 -2n +1+4n
=n4 +2n +1,
AC =(n +1) =n4 +2n +1,
∴AB +BC = AC .
∴△ABC直角三角形,边AC所对的角是直角.
先确定AB、BC、AC、
的大小
例3 在正方形ABCD中,F是CD的中点,E为BC上一点,且CE= CB,试判断AF与EF的
位置关系,并说明理由.
解:AF⊥EF.理由:设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
一、直角三角形的判定(勾股定理的逆定理):
文字语言:
如果三角形三边长a,b,c满足a +b =c ,
那么这个三角形是直角三角形
几何语言:
∵ a +b =c
∴ ∠C=90°(c为斜边)
a
b
c
应用:
用来判定三角形的形状。
1. 三个数满足a +b =c ,
2. 三个数都是正整数。
二、勾股数满足的条件是:
知识小结
2.如果线段a,b,c能组成直角三角形, 则它们的比可能是 ( )
A.3:4:7 B.5:12:13 C.1:2:4 D.1:3:5
当堂训练
B
1.已知 ABC中, BC=41, AC=40, AB=9, 则此三角形为_______三角形, ______是最大角.
三角形的三边分别是a,b,c, 且满足等式 (a+b)2-c2=2ab, 则此三角形是 ( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 等腰直角三角形
A
直角
∠A
4、下列各组数是勾股数的是( )
A.6,8,10 B.7,8,9
C.0.3,0.4,0.5 D.52,122,132
A
方法点拨:根据勾股数的定义,勾股数必须为正整数,先排除小数,再计算最长边的平方是否等于其他两边的平方和即可.
5、如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3 cm,BC=4 cm,求△ABC的面积.
解: ∵ S△ACD=30 cm2,DC=12 cm.
∴ AC=5 cm,
又∵
∴△ABC是直角三角形, ∠B是直角.
∴
D
C
B
A
①②④
6.若△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B-∠C;②a2=(b+c)(b-c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:12:13.其中能判定△ABC是直角三角形的是_____________.(填序号)
7.如图,四边形ABCD中,已知AB=3,BC=4,CD=12,DA=13, 且∠ABC=900,求这个四边形的面积.
解:如图,连接AC.
在Rt△ABC中,由勾股定理,
得 AC2=AB2+BC2,∴AC=5,
又∵ CD=12cm,AD=13cm
∴ AD2=CD2+AC2,∴△ACD是直角三角形.
S四边形ABCD=SRt△ABC+SRt△ACD= (3×4+5×12)÷2=36.
变式:如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.
解:如图,连接BD.
在Rt△ABD中,由勾股定理,
得 BD2=AB2+AD2,∴BD=5m,
又∵ CD=12cm,BC=13cm
∴ BC2=CD2+BD2,∴△BDC是直角三角形, ∠CDB是直角.
S四边形ABCD=SRt△BCD-SRt△ABD= BD CD- AB AD
= (5×12-3×4)=24 m2.
C
B
A
D
8、探索勾股数的规律:观察下列各组数:
(3,4,5),(5,12,13),(7,24,25),
(9,40,41)...可发现,
...请写出第五个数组:___________
(11,60,61)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
