12.3 角平分线的性质(1) 课件(共29张PPT)
文档属性
| 名称 | 12.3 角平分线的性质(1) 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 21:23:25 | ||
图片预览






文档简介
(共29张PPT)
12.3 角平分线的性质(1)
人教版八年级上册
知识回顾
角平分线的定义:
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
O
A
B
C
如图,OC是∠AOB的平分线.
∠AOC=∠BOC= ∠AOB.
教学目标
1.会用尺规作图法作一个角的平分线,知道作法的理论依据.
2.探究并证明角平分线的性质.
3.会用角平分线的性质解决实际问题.
新知导入
在生产、生活中我们经常需要平分一个角,已到达美观、实用的目的,所以我们今天的学习就从如何准确的平分一个角开始。
新知探究
知识点 1
角平分线的画法
问题1:在纸上画一个角,你能得到这个角的平分线吗?
用量角器度量,也可用折纸的方法.
很明显这些方法都一些不足,例如量角器度数的误差,书本上的角折叠不方便等,其实使用我们的直尺和圆规就能够画出任意角的平分线。按照下面的步骤我们一起来做一遍吧
新知讲解
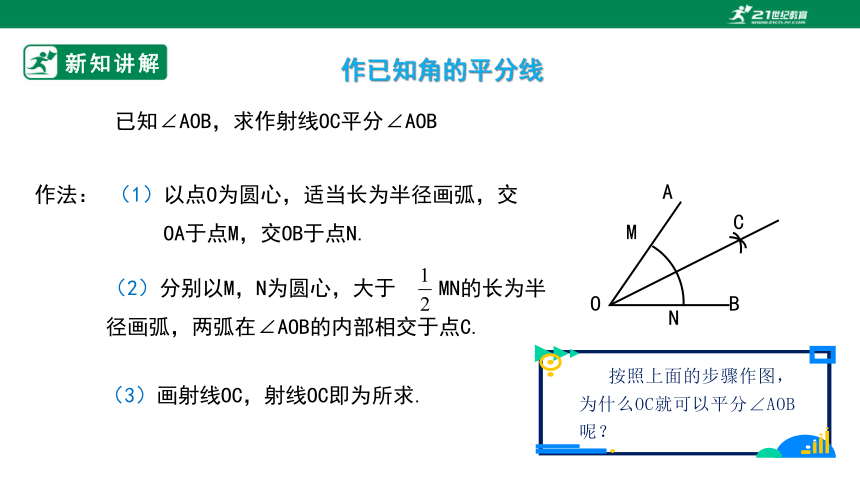
作法: (1)以点O为圆心,适当长为半径画弧,交
OA于点M,交OB于点N.
(2)分别以M,N为圆心,大于 MN的长为半 径画弧,两弧在∠AOB的内部相交于点C.
C
B
N
O
M
A
(3)画射线OC,射线OC即为所求.
作已知角的平分线
已知∠AOB,求作射线OC平分∠AOB
按照上面的步骤作图,为什么OC就可以平分∠AOB呢?
新知探究
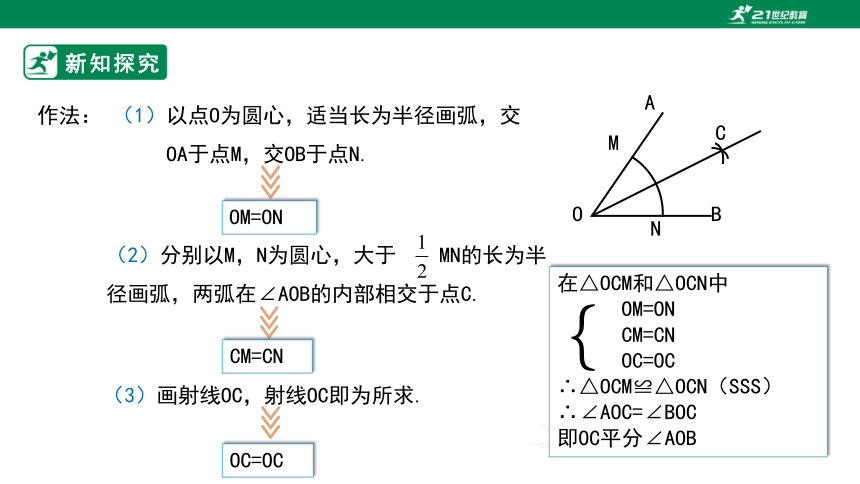
作法: (1)以点O为圆心,适当长为半径画弧,交
OA于点M,交OB于点N.
C
B
N
O
M
A
OM=ON
(2)分别以M,N为圆心,大于 MN的长为半 径画弧,两弧在∠AOB的内部相交于点C.
CM=CN
(3)画射线OC,射线OC即为所求.
OC=OC
在△OCM和△OCN中
OM=ON
CM=CN
OC=OC
∴△OCM≌△OCN(SSS)
∴∠AOC=∠BOC
即OC平分∠AOB
{
新知探究
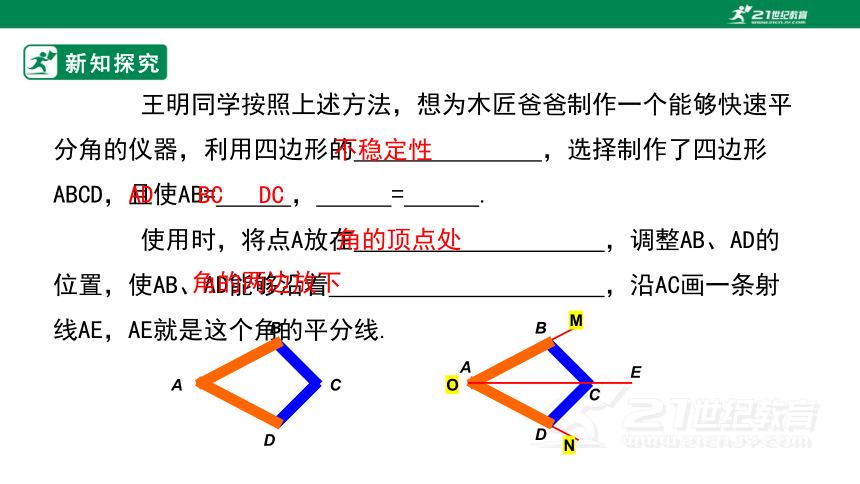
王明同学按照上述方法,想为木匠爸爸制作一个能够快速平分角的仪器,利用四边形的 ,选择制作了四边形ABCD,且使AB= , = .
使用时,将点A放在 ,调整AB、AD的位置,使AB、AD能够沿着 ,沿AC画一条射线AE,AE就是这个角的平分线.
不稳定性
AD
BC
DC
角的顶点处
角的两边放下
A
B
C
D
A
B
C
D
E
新知小结
注意:(1)以“适当长为半径”是为了方便画图,不能太长,也不能太短.
C
B
N
O
M
A
(3)应该在角的内部找所作两弧的交点,因为所作的射线为角的平分线,而角的平分线应该在角的内部.
(4)“画射线OC ”不能说成“连接OC ”,因为连接OC得到的是线段,而角的平分线是一条射线.
(2)“以大于 MN的长为半径画弧”是因为小于MN的长为半径画弧时两弧没有交点,等于 MN的长为半径画弧时不容易操作.
新知探究
角平分线的性质
知识点 2
在刚才我们一起画的∠AOB的平分线OC上任取一点P,过点P画出OA,OB的垂线,分别记垂足为D,E,测量PD,PE并作比较,你得到什么结论?在OC上再取几个点试一试.
经过测量发现,PD=PE,在OC上再取几个点,都能得到同样的结论.
猜想:角的平分线上的点到角的两边的距离相等.
新知探究
已知:如图, ∠AOC= ∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.
求证:PD=PE.
P
A
O
B
C
D
E
证明:
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO= ∠PEO=90 °.
在△PDO和△PEO中,
∠PDO= ∠PEO,
∠AOC= ∠BOC,
OP= OP,
∴ △PDO ≌△PEO(AAS).
∴PD=PE.
角的平分线上的点到角的两边的距离相等.
验证猜想
已知
求证
新知小结
性质定理:角的平分线上的点到角的两边的距离相等.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等.
应用格式:
∵OP 是∠AOB的平分线,
∴PD = PE
推理的理由有三个,必须写完全,不能少了任何一个.
PD⊥OA, PE⊥OB,
B
A
D
O
P
E
C
角的平分线的性质
新知小结
证明几何命题的一般步骤:
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用符号表示已知和求证;
(3)经过分析,找出由已知推出要证的结论的途径,写出证明过程.
当题目需要自主画图时,注意:
(1)所画图形应符合题意,并具有一般性和代表性.在画图的时候要考虑是否存在不同的情形,若存在,则要分别画出图形,再分别进行证明;
(2)证明过程中的每一步推理都要有依据,依据可以是已知条件、定义、定理等.
新知典例
例1 求证:三角形的一边的两端点到这条边上的中线所在直线的距离相等.
解:已知:如图所示,AD为△ABC的中线,且CF⊥AD于点F,BE⊥AD交AD的延长线于点E.
求证:BE=CF.
可先将命题改写成“如果……那么……”的形式,然后确定已知和求证
如果 ,那么
三角形的一边有一条中线
这条边的两个端点到中线的距离相等
新知典例
证明:∵AD为△ABC的中线,∴BD=CD.
∵BE⊥AD交AD的延长线于点E,CF⊥AD,
∴∠BED=∠CFD=90°.
在△BED和△CFD中
∠BED=∠CFD,
∠BDE=∠CDF,
BD=CD,
∴△BED≌△CFD(AAS),
∴BE=CF.
课堂练习
1.判一判:(1)∵ 如下左图,AD平分∠BAC(已知),
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
(2)∵ 如上右图, DC⊥AC,DB⊥AB (已知).
∴ = ,
( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
缺少“垂直距离”这一条件
缺少“角平分线”这一条件
新知典例
例2、如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长.
解:∵BD平分∠ABC交AC于点D,DE⊥AB,DF⊥BC,
∴DE=DF,
∵AB=6,BC=8,S△ABC=28,
∴S△ABC=S△ABD+S△BCD= AB DE+ BC DF
= DE (AB+BC)=28
即DE(6+8)=28,
∴DE=4.
课堂练习
2.如图,CD是Rt△ABC的角平分线,∠A=90°,AD=4,BC=7,则△BCD的面积为 .
14
解:过D作DE⊥BC于E,
∵CD是Rt△ABC的角平分线,∠A=90°,AD=4,
∴DE=AD=4,
∵BC=7,
∴△BCD的面积= BC DE= 7×4=14
新知典例
例3 如图,在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=8,CD=4,则四边形ABCD的面积是 .
28
解:过点D作DE⊥BA的延长线于点E,如图所示.
∵BD平分∠ABC,
∴DE=DC=4,
∴S四边形ABCD=S△ABD+S△BCD,
= AB DE+ BC CD,
= ×6×4+ ×8×4,
=28.
┐
E
课堂练习
A
B
C
P
3.如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4, AB=14.
则点P到AB的距离为_______.
D
4
此垂线为角平分线性质相关题目常见辅助线
课堂练习
1.如图,△ABC的三边AC、BC、AB的长分别是8、12、16,点O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC的值为( )
A.4:3:2 B.1:2:3
C.2:3:4 D.3:4:5
A
课堂练习
2.某镇要在三条公路围成的一块三角形平地内修建一个砂石场,如图,要使这个砂石场到三条公路的距离相等,则可供选择的地址( )
A.仅有一处 B.有四处
C.有七处 D.有无数处
A
课堂练习
3.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB,垂足为E,若AB=8cm,则△DEB的周长为( )
A.10cm B.7cm C.8cm D.不能确定
课堂练习
解析:在△ABC中,∠C=90°, ∴DC⊥AC.
∵DE⊥AB,AD平分∠CAB, ∴DC=DE.
在Rt△ACD和Rt△AED中, AD=AD,
DC=DE,
∴Rt△ACD≌Rt△AED(HL), ∴AC=AE.
∵AC=BC,∴AE=BC,
∴△DEB的周长=DE+DB+ EB=DC+DB+EB=BC+EB=AE+EB=AB=8cm.
课堂练习
4.如图,已知AD∥BC,P是∠BAD与∠ABC的平分线的交点,PE⊥AB于E,且PE=3,求AD与BC之间的距离.
解:过点P作MN⊥AD于点M,交BC于点N.
∵ AD∥BC,
∴ MN⊥BC,MN的长即为AD与BC之间的距离.
∵ AP平分∠BAD, PM⊥AD , PE⊥AB,
∴ PM= PE.
同理, PN= PE.
∴ PM= PN= PE=3.
∴ MN=6.即AD与BC之间的距离为6.
课堂总结
角的平分线的性质
会用尺规作图法画出一个已知角的平分线
性质
应用
角的平分线上的点到角的两边的距离相等
利用角的平分线的性质解决实际问题
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
12.3 角平分线的性质(1)
人教版八年级上册
知识回顾
角平分线的定义:
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
O
A
B
C
如图,OC是∠AOB的平分线.
∠AOC=∠BOC= ∠AOB.
教学目标
1.会用尺规作图法作一个角的平分线,知道作法的理论依据.
2.探究并证明角平分线的性质.
3.会用角平分线的性质解决实际问题.
新知导入
在生产、生活中我们经常需要平分一个角,已到达美观、实用的目的,所以我们今天的学习就从如何准确的平分一个角开始。
新知探究
知识点 1
角平分线的画法
问题1:在纸上画一个角,你能得到这个角的平分线吗?
用量角器度量,也可用折纸的方法.
很明显这些方法都一些不足,例如量角器度数的误差,书本上的角折叠不方便等,其实使用我们的直尺和圆规就能够画出任意角的平分线。按照下面的步骤我们一起来做一遍吧
新知讲解
作法: (1)以点O为圆心,适当长为半径画弧,交
OA于点M,交OB于点N.
(2)分别以M,N为圆心,大于 MN的长为半 径画弧,两弧在∠AOB的内部相交于点C.
C
B
N
O
M
A
(3)画射线OC,射线OC即为所求.
作已知角的平分线
已知∠AOB,求作射线OC平分∠AOB
按照上面的步骤作图,为什么OC就可以平分∠AOB呢?
新知探究
作法: (1)以点O为圆心,适当长为半径画弧,交
OA于点M,交OB于点N.
C
B
N
O
M
A
OM=ON
(2)分别以M,N为圆心,大于 MN的长为半 径画弧,两弧在∠AOB的内部相交于点C.
CM=CN
(3)画射线OC,射线OC即为所求.
OC=OC
在△OCM和△OCN中
OM=ON
CM=CN
OC=OC
∴△OCM≌△OCN(SSS)
∴∠AOC=∠BOC
即OC平分∠AOB
{
新知探究
王明同学按照上述方法,想为木匠爸爸制作一个能够快速平分角的仪器,利用四边形的 ,选择制作了四边形ABCD,且使AB= , = .
使用时,将点A放在 ,调整AB、AD的位置,使AB、AD能够沿着 ,沿AC画一条射线AE,AE就是这个角的平分线.
不稳定性
AD
BC
DC
角的顶点处
角的两边放下
A
B
C
D
A
B
C
D
E
新知小结
注意:(1)以“适当长为半径”是为了方便画图,不能太长,也不能太短.
C
B
N
O
M
A
(3)应该在角的内部找所作两弧的交点,因为所作的射线为角的平分线,而角的平分线应该在角的内部.
(4)“画射线OC ”不能说成“连接OC ”,因为连接OC得到的是线段,而角的平分线是一条射线.
(2)“以大于 MN的长为半径画弧”是因为小于MN的长为半径画弧时两弧没有交点,等于 MN的长为半径画弧时不容易操作.
新知探究
角平分线的性质
知识点 2
在刚才我们一起画的∠AOB的平分线OC上任取一点P,过点P画出OA,OB的垂线,分别记垂足为D,E,测量PD,PE并作比较,你得到什么结论?在OC上再取几个点试一试.
经过测量发现,PD=PE,在OC上再取几个点,都能得到同样的结论.
猜想:角的平分线上的点到角的两边的距离相等.
新知探究
已知:如图, ∠AOC= ∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.
求证:PD=PE.
P
A
O
B
C
D
E
证明:
∵ PD⊥OA,PE⊥OB,
∴ ∠PDO= ∠PEO=90 °.
在△PDO和△PEO中,
∠PDO= ∠PEO,
∠AOC= ∠BOC,
OP= OP,
∴ △PDO ≌△PEO(AAS).
∴PD=PE.
角的平分线上的点到角的两边的距离相等.
验证猜想
已知
求证
新知小结
性质定理:角的平分线上的点到角的两边的距离相等.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等.
应用格式:
∵OP 是∠AOB的平分线,
∴PD = PE
推理的理由有三个,必须写完全,不能少了任何一个.
PD⊥OA, PE⊥OB,
B
A
D
O
P
E
C
角的平分线的性质
新知小结
证明几何命题的一般步骤:
(1)明确命题中的已知和求证;
(2)根据题意,画出图形,并用符号表示已知和求证;
(3)经过分析,找出由已知推出要证的结论的途径,写出证明过程.
当题目需要自主画图时,注意:
(1)所画图形应符合题意,并具有一般性和代表性.在画图的时候要考虑是否存在不同的情形,若存在,则要分别画出图形,再分别进行证明;
(2)证明过程中的每一步推理都要有依据,依据可以是已知条件、定义、定理等.
新知典例
例1 求证:三角形的一边的两端点到这条边上的中线所在直线的距离相等.
解:已知:如图所示,AD为△ABC的中线,且CF⊥AD于点F,BE⊥AD交AD的延长线于点E.
求证:BE=CF.
可先将命题改写成“如果……那么……”的形式,然后确定已知和求证
如果 ,那么
三角形的一边有一条中线
这条边的两个端点到中线的距离相等
新知典例
证明:∵AD为△ABC的中线,∴BD=CD.
∵BE⊥AD交AD的延长线于点E,CF⊥AD,
∴∠BED=∠CFD=90°.
在△BED和△CFD中
∠BED=∠CFD,
∠BDE=∠CDF,
BD=CD,
∴△BED≌△CFD(AAS),
∴BE=CF.
课堂练习
1.判一判:(1)∵ 如下左图,AD平分∠BAC(已知),
∴ = ,( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
(2)∵ 如上右图, DC⊥AC,DB⊥AB (已知).
∴ = ,
( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
缺少“垂直距离”这一条件
缺少“角平分线”这一条件
新知典例
例2、如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长.
解:∵BD平分∠ABC交AC于点D,DE⊥AB,DF⊥BC,
∴DE=DF,
∵AB=6,BC=8,S△ABC=28,
∴S△ABC=S△ABD+S△BCD= AB DE+ BC DF
= DE (AB+BC)=28
即DE(6+8)=28,
∴DE=4.
课堂练习
2.如图,CD是Rt△ABC的角平分线,∠A=90°,AD=4,BC=7,则△BCD的面积为 .
14
解:过D作DE⊥BC于E,
∵CD是Rt△ABC的角平分线,∠A=90°,AD=4,
∴DE=AD=4,
∵BC=7,
∴△BCD的面积= BC DE= 7×4=14
新知典例
例3 如图,在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=8,CD=4,则四边形ABCD的面积是 .
28
解:过点D作DE⊥BA的延长线于点E,如图所示.
∵BD平分∠ABC,
∴DE=DC=4,
∴S四边形ABCD=S△ABD+S△BCD,
= AB DE+ BC CD,
= ×6×4+ ×8×4,
=28.
┐
E
课堂练习
A
B
C
P
3.如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4, AB=14.
则点P到AB的距离为_______.
D
4
此垂线为角平分线性质相关题目常见辅助线
课堂练习
1.如图,△ABC的三边AC、BC、AB的长分别是8、12、16,点O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC的值为( )
A.4:3:2 B.1:2:3
C.2:3:4 D.3:4:5
A
课堂练习
2.某镇要在三条公路围成的一块三角形平地内修建一个砂石场,如图,要使这个砂石场到三条公路的距离相等,则可供选择的地址( )
A.仅有一处 B.有四处
C.有七处 D.有无数处
A
课堂练习
3.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB,垂足为E,若AB=8cm,则△DEB的周长为( )
A.10cm B.7cm C.8cm D.不能确定
课堂练习
解析:在△ABC中,∠C=90°, ∴DC⊥AC.
∵DE⊥AB,AD平分∠CAB, ∴DC=DE.
在Rt△ACD和Rt△AED中, AD=AD,
DC=DE,
∴Rt△ACD≌Rt△AED(HL), ∴AC=AE.
∵AC=BC,∴AE=BC,
∴△DEB的周长=DE+DB+ EB=DC+DB+EB=BC+EB=AE+EB=AB=8cm.
课堂练习
4.如图,已知AD∥BC,P是∠BAD与∠ABC的平分线的交点,PE⊥AB于E,且PE=3,求AD与BC之间的距离.
解:过点P作MN⊥AD于点M,交BC于点N.
∵ AD∥BC,
∴ MN⊥BC,MN的长即为AD与BC之间的距离.
∵ AP平分∠BAD, PM⊥AD , PE⊥AB,
∴ PM= PE.
同理, PN= PE.
∴ PM= PN= PE=3.
∴ MN=6.即AD与BC之间的距离为6.
课堂总结
角的平分线的性质
会用尺规作图法画出一个已知角的平分线
性质
应用
角的平分线上的点到角的两边的距离相等
利用角的平分线的性质解决实际问题
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
