人教版七年级下册5.2.2平行线的判定课件(共16张PPT)
文档属性
| 名称 | 人教版七年级下册5.2.2平行线的判定课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 09:17:55 | ||
图片预览





文档简介
(共16张PPT)
5.2.2平行线的判定
人教版七年级下册
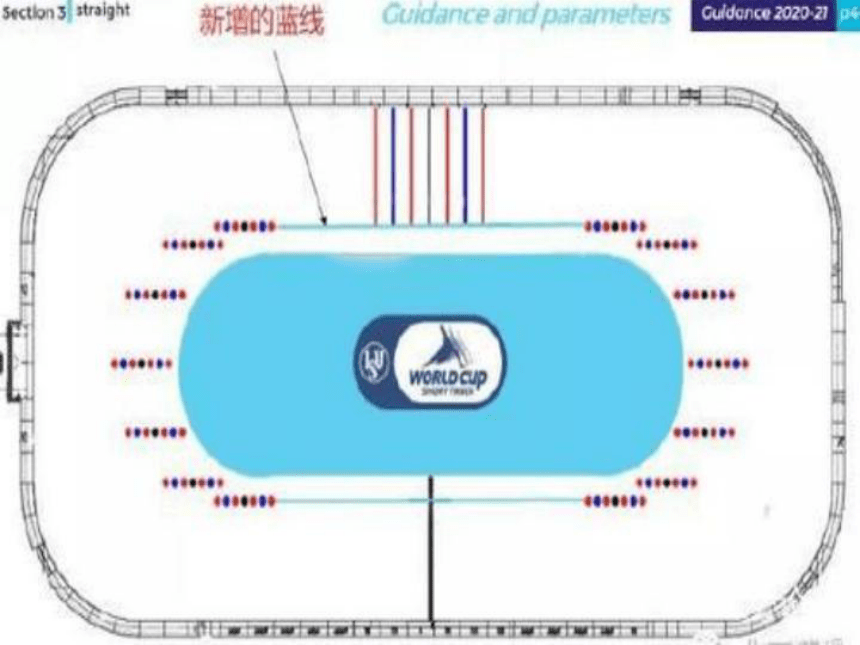
问题1、新增的蓝线与这些彩线有怎样的位置关系?
问题2、观察这些彩线有怎样的位置关系?
为什么这些彩线与蓝线保持垂直就可以保证平行呢?
1.探索并掌握平行线的判定方法;
2.会用符号语言表示平行线的判定方法;
3.应用所学知识解决简单的实际问题;
4. 体会研究几何图形的意义。
学习目标
短道速滑比赛时,运动员武大靖位于点P的位置,某个时间段内,他旁边意大利选手的滑行路线为AB,正好与武大靖的滑行路线CD平行,你能帮武大靖画出他的滑行路线吗?
B
01
情境引入 探究新知
A
1
A
C
.
P
2
B
D
根据画图的过程,思考下列问题:
(1)∠1和∠2是什么位置关系的角?
(2)直尺起到什么作用?
(3) ∠1和∠2有什么数量关系?为什么?
动态演示
01
归纳总结 得出判定
两条直线被第三条直线所截,如果同位角相等,那么两条直线平行。
B
A
C
D
1
2
过直线外一点画已知直线的平行线依据是什么?
02
自主探究 形成定理
探究2 如图,如果∠1=∠2,那么a与b平行吗?
解:平行
理由如下:因为 ∠1=∠3(对顶角相等)
又因为 ∠1=∠2(已知)
所以 ∠2=∠3(等量代换)
所以 a∥b(同位角相等,两直线平行)
3
02
自主探究 形成定理
探究3 如图,如果∠1+∠2=180°,那么a与b平行吗?
a
b
c
解:平行
理由如下:因为 ∠1+∠3 =180° (平角的定义)
又因为 ∠1+∠ 2=180° (已知)
所以 ∠2=∠3(等量代换)
所以 a∥b(同位角相等,两直线平行)
3
(1)∵∠1=∠B(已知)
∴__∥__(
(4)∵∠_ ∠_(已知)
∴AB∥CD( )
AD BC 同位角相等,两直线平行)
(2)∵∠1=∠D(已知)
∴ ∥ ( )
(3)∵∠B+∠BAD=180°(已知)
∴ ∥ ( )
3 = 5
内错角相等,两直线平行
AB DC 内错角相等,两直线平行
AD BC 同旁内角互补,两直线平行
如图:
02
跟踪练习 达成目标
为什么这些彩线与蓝线保持垂直就可以保证平行呢?
如图, 在同一平面内,b⊥a,c⊥ a,则 b ∥c .
b
c
a
1
2
解:∵ b⊥a,c⊥ a (已知)
∴∠1=∠2 = 90 ° (垂直的定义)
∴b ∥ c(同位角相等,两直线平行)
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。
你能用这种判定方法找一找生活中的平行线吗?
04
小结
本节课你有哪些收获?
归纳总结 反思提升
《平行线的判定》评测练习
基础达标:
1(1)如果∠1=∠2,可以判定哪两条直线平行 根据是什么?
(2)如果∠3=∠4,可以判定哪两条直线平行 根据是什么?
(3)如果∠2=∠5,可以判定哪两条直线平行 根据是什么?
2.填空
①∵∠1 = (已知)∴ AB∥CE( )
②∵∠1 +____=180°(已知)∴ CD∥BF( )
③∵∠1 +∠5 =180 ° (已知)∴ _____∥_____( )
④∵∠4 + =180 ° (已知)∴ CE∥AB(
能力提升:3、已知:∠3=45 °,∠1与∠2互余,求证:AB//CD.
思维拓展:在短道速滑比赛过程中,武大靖在直赛道上滑行时,不慎向右偏转5°,为了与原来的方向保持一致,他该应如何调整滑行方向?
5.2.2平行线的判定
人教版七年级下册
问题1、新增的蓝线与这些彩线有怎样的位置关系?
问题2、观察这些彩线有怎样的位置关系?
为什么这些彩线与蓝线保持垂直就可以保证平行呢?
1.探索并掌握平行线的判定方法;
2.会用符号语言表示平行线的判定方法;
3.应用所学知识解决简单的实际问题;
4. 体会研究几何图形的意义。
学习目标
短道速滑比赛时,运动员武大靖位于点P的位置,某个时间段内,他旁边意大利选手的滑行路线为AB,正好与武大靖的滑行路线CD平行,你能帮武大靖画出他的滑行路线吗?
B
01
情境引入 探究新知
A
1
A
C
.
P
2
B
D
根据画图的过程,思考下列问题:
(1)∠1和∠2是什么位置关系的角?
(2)直尺起到什么作用?
(3) ∠1和∠2有什么数量关系?为什么?
动态演示
01
归纳总结 得出判定
两条直线被第三条直线所截,如果同位角相等,那么两条直线平行。
B
A
C
D
1
2
过直线外一点画已知直线的平行线依据是什么?
02
自主探究 形成定理
探究2 如图,如果∠1=∠2,那么a与b平行吗?
解:平行
理由如下:因为 ∠1=∠3(对顶角相等)
又因为 ∠1=∠2(已知)
所以 ∠2=∠3(等量代换)
所以 a∥b(同位角相等,两直线平行)
3
02
自主探究 形成定理
探究3 如图,如果∠1+∠2=180°,那么a与b平行吗?
a
b
c
解:平行
理由如下:因为 ∠1+∠3 =180° (平角的定义)
又因为 ∠1+∠ 2=180° (已知)
所以 ∠2=∠3(等量代换)
所以 a∥b(同位角相等,两直线平行)
3
(1)∵∠1=∠B(已知)
∴__∥__(
(4)∵∠_ ∠_(已知)
∴AB∥CD( )
AD BC 同位角相等,两直线平行)
(2)∵∠1=∠D(已知)
∴ ∥ ( )
(3)∵∠B+∠BAD=180°(已知)
∴ ∥ ( )
3 = 5
内错角相等,两直线平行
AB DC 内错角相等,两直线平行
AD BC 同旁内角互补,两直线平行
如图:
02
跟踪练习 达成目标
为什么这些彩线与蓝线保持垂直就可以保证平行呢?
如图, 在同一平面内,b⊥a,c⊥ a,则 b ∥c .
b
c
a
1
2
解:∵ b⊥a,c⊥ a (已知)
∴∠1=∠2 = 90 ° (垂直的定义)
∴b ∥ c(同位角相等,两直线平行)
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行。
你能用这种判定方法找一找生活中的平行线吗?
04
小结
本节课你有哪些收获?
归纳总结 反思提升
《平行线的判定》评测练习
基础达标:
1(1)如果∠1=∠2,可以判定哪两条直线平行 根据是什么?
(2)如果∠3=∠4,可以判定哪两条直线平行 根据是什么?
(3)如果∠2=∠5,可以判定哪两条直线平行 根据是什么?
2.填空
①∵∠1 = (已知)∴ AB∥CE( )
②∵∠1 +____=180°(已知)∴ CD∥BF( )
③∵∠1 +∠5 =180 ° (已知)∴ _____∥_____( )
④∵∠4 + =180 ° (已知)∴ CE∥AB(
能力提升:3、已知:∠3=45 °,∠1与∠2互余,求证:AB//CD.
思维拓展:在短道速滑比赛过程中,武大靖在直赛道上滑行时,不慎向右偏转5°,为了与原来的方向保持一致,他该应如何调整滑行方向?
