2.4估算 课件 课件(共20张PPT)
文档属性
| 名称 | 2.4估算 课件 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 421.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 09:52:47 | ||
图片预览








文档简介
(共20张PPT)
某地开辟了一块长方形荒地,新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400000m2.
(1)公园的宽大约是多少?它有1000m吗?
1000
2000
S=400000
∵2000×1000=2000000 >400000,
∴公园的宽没有1 000m.
情境导入
(2)如果要求结果精确到10米,
它的宽大约是多少?
2.4 估算
1.能通过估算,检验计算结果的合理性;
2.能估计一个无理数的大致范围,并能通过估算比较两个数的大小;
3.掌握估算的方法,形成估算意识。
学习目标(1分钟)
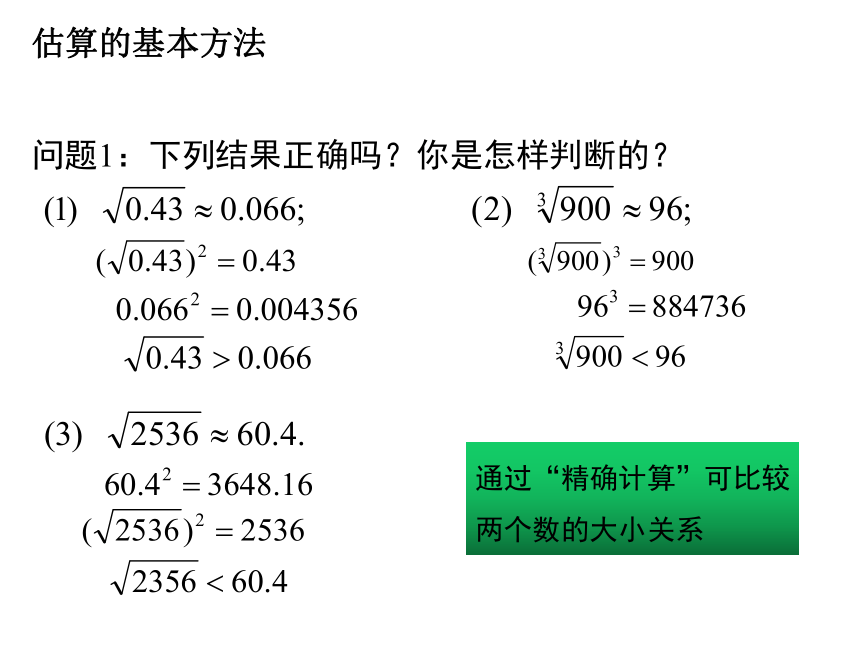
问题1:下列结果正确吗?你是怎样判断的?
通过“精确计算”可比较
两个数的大小关系
估算的基本方法
通过“估算”也可比较
两个数的大小关系
确定无理数 的大小的方法和关键分别是什么?
(1)先确定整数部分:
首先找到两个整数m和n,使 ,则得
,确定整数部分。
关键:依据平方根、立方根
(2) 确定小数点后有一位、两位等小数部分:
重复(1)的做法进行若干次,达到精确度的要求。
方法:夹逼法
方法小结
问题2:你能估算 的大小吗?(结果精确到1)
解:∵9 =729<900<1000=10
∴ < <
∴9< <10
∵9.5 = 857.375,9.6 =884.736,9.7 =912.673
∴9.6< <9.7
∴ ≈10
完成引例中的问题:
1.引例:设公园的宽为x m,则长为2x m,依题意可得
_____________ 解得 _______________
(1)公园的宽大约为________,有1000m吗? ____
(2)如果要求结果精确到10m,它的宽大约是______。
(3)该公园中心有一个圆形花圃,它的面积是800m ,你能估计它的半径吗?(结果精确到1m)
没有
447.2米
450米
解:依题意得 故它的半径约16米。
自学检测1(5分钟)
1.P34随堂训练T1 估算下列数的大小:
2. P34 数学理解T4 下列计算结果正确吗?
解:(1)错.因为 显然大于10;
(1) ≈9.5
3.设a= ,a在两相邻整数之间,则这两个整数是( )
A.2和3 B.4和5 C.7和8 D.8和9
C
1.认真阅读例题,理解解题思路,掌握题中比较两数的大小的方法。
2.小明在比较两数时用了什么方法?
3. 对于P34两个无理数的比较,你有更好的方法比较大小吗?
自学指导2 (1分钟)
认真阅读P33例题至P34议一议,解决以下几个问题
作差法
两边平方,然后比较大小
∵5.6 =31.36< =32 ∴ >5.6
例2:生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的 ,则梯子比较稳定.现有一长为6 m的梯子,当梯子稳定摆放时,它的顶端能达到5.6m高的墙头吗
解:设梯子稳定摆放时的高度为x m,此时梯子底端离墙的距离恰为梯子长度的 ,根据勾股定理得
6
所以梯子稳定摆放时,它的顶端能够达到5.6m高的墙头.
用两种方法比较
自学检测2(5分钟)
2.通过估算,比较下面各组数的大小。
解:(1)∵2.52=6.25
∴2.5= >
(2)作差得
1.大于 且小于 的整数是________。
2
小结(1分钟)
1、掌握夹逼法估计一个无理数的大致范围。
依据:
2、会通过估算比较两个数的大小;
3、会通过估算检验计算结果的合理性。
当堂训练(14分钟)
2.通过估算,比较下面各组数的大小:
1.估算 (精确到0.1)≈__________
5.1
易错点:比较无理数的大小时要比较其结果的大小,不能仅比较被开方数的大小。
4.完成P35问题解决 T5
5.(选做题)完成P35问题解决 T6
3.已知a是 的整数部分,b是 的小数部分,则2a+b=__________
解:∵4< <5
∴a=4,b= -4
∴2a+b=2×4+ -4
= +4
5.解:设梯子的长度为x米,梯子底端与墙的距离是 米,依题意得
4.解:设圆柱的高为x米,则底面半径为0.5x米,依题意得
∴x≈4
答:圆柱的高为4米。
6.(选做题)先阅读理解,再回答问题:
以此类推,我们会发现 的整数部分是多少呢?并说明理由。
板书设计
2.4 估算
1、确定无理数 的大小的方法
2、平方法、作差法、作商法比较两个数的大小;
3、通过估算检验计算结果的合理性。
方法:夹逼法
依据:
习题2.6 T1(1)
习题2.6 T2(2)
解:(1)∵6 =216,7 =343,而216<260<343
∴
又∵6.3 <260<6.3 ∴6.3< <6.4
∴
解:∵3.85 =14.8225<15,
∴
某地开辟了一块长方形荒地,新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400000m2.
(1)公园的宽大约是多少?它有1000m吗?
1000
2000
S=400000
∵2000×1000=2000000 >400000,
∴公园的宽没有1 000m.
情境导入
(2)如果要求结果精确到10米,
它的宽大约是多少?
2.4 估算
1.能通过估算,检验计算结果的合理性;
2.能估计一个无理数的大致范围,并能通过估算比较两个数的大小;
3.掌握估算的方法,形成估算意识。
学习目标(1分钟)
问题1:下列结果正确吗?你是怎样判断的?
通过“精确计算”可比较
两个数的大小关系
估算的基本方法
通过“估算”也可比较
两个数的大小关系
确定无理数 的大小的方法和关键分别是什么?
(1)先确定整数部分:
首先找到两个整数m和n,使 ,则得
,确定整数部分。
关键:依据平方根、立方根
(2) 确定小数点后有一位、两位等小数部分:
重复(1)的做法进行若干次,达到精确度的要求。
方法:夹逼法
方法小结
问题2:你能估算 的大小吗?(结果精确到1)
解:∵9 =729<900<1000=10
∴ < <
∴9< <10
∵9.5 = 857.375,9.6 =884.736,9.7 =912.673
∴9.6< <9.7
∴ ≈10
完成引例中的问题:
1.引例:设公园的宽为x m,则长为2x m,依题意可得
_____________ 解得 _______________
(1)公园的宽大约为________,有1000m吗? ____
(2)如果要求结果精确到10m,它的宽大约是______。
(3)该公园中心有一个圆形花圃,它的面积是800m ,你能估计它的半径吗?(结果精确到1m)
没有
447.2米
450米
解:依题意得 故它的半径约16米。
自学检测1(5分钟)
1.P34随堂训练T1 估算下列数的大小:
2. P34 数学理解T4 下列计算结果正确吗?
解:(1)错.因为 显然大于10;
(1) ≈9.5
3.设a= ,a在两相邻整数之间,则这两个整数是( )
A.2和3 B.4和5 C.7和8 D.8和9
C
1.认真阅读例题,理解解题思路,掌握题中比较两数的大小的方法。
2.小明在比较两数时用了什么方法?
3. 对于P34两个无理数的比较,你有更好的方法比较大小吗?
自学指导2 (1分钟)
认真阅读P33例题至P34议一议,解决以下几个问题
作差法
两边平方,然后比较大小
∵5.6 =31.36< =32 ∴ >5.6
例2:生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的 ,则梯子比较稳定.现有一长为6 m的梯子,当梯子稳定摆放时,它的顶端能达到5.6m高的墙头吗
解:设梯子稳定摆放时的高度为x m,此时梯子底端离墙的距离恰为梯子长度的 ,根据勾股定理得
6
所以梯子稳定摆放时,它的顶端能够达到5.6m高的墙头.
用两种方法比较
自学检测2(5分钟)
2.通过估算,比较下面各组数的大小。
解:(1)∵2.52=6.25
∴2.5= >
(2)作差得
1.大于 且小于 的整数是________。
2
小结(1分钟)
1、掌握夹逼法估计一个无理数的大致范围。
依据:
2、会通过估算比较两个数的大小;
3、会通过估算检验计算结果的合理性。
当堂训练(14分钟)
2.通过估算,比较下面各组数的大小:
1.估算 (精确到0.1)≈__________
5.1
易错点:比较无理数的大小时要比较其结果的大小,不能仅比较被开方数的大小。
4.完成P35问题解决 T5
5.(选做题)完成P35问题解决 T6
3.已知a是 的整数部分,b是 的小数部分,则2a+b=__________
解:∵4< <5
∴a=4,b= -4
∴2a+b=2×4+ -4
= +4
5.解:设梯子的长度为x米,梯子底端与墙的距离是 米,依题意得
4.解:设圆柱的高为x米,则底面半径为0.5x米,依题意得
∴x≈4
答:圆柱的高为4米。
6.(选做题)先阅读理解,再回答问题:
以此类推,我们会发现 的整数部分是多少呢?并说明理由。
板书设计
2.4 估算
1、确定无理数 的大小的方法
2、平方法、作差法、作商法比较两个数的大小;
3、通过估算检验计算结果的合理性。
方法:夹逼法
依据:
习题2.6 T1(1)
习题2.6 T2(2)
解:(1)∵6 =216,7 =343,而216<260<343
∴
又∵6.3 <260<6.3 ∴6.3< <6.4
∴
解:∵3.85 =14.8225<15,
∴
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
