2.1认识无理数(1) 课件(共15张PPT)
文档属性
| 名称 | 2.1认识无理数(1) 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 230.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-12 09:09:59 | ||
图片预览




文档简介
(共15张PPT)
1.在初一我们学习了“数怎么不够用了”,从而引入了 数,进而把数的范围扩充到了 数.
2. 和 统称为有理数。
3.整数可分为 、 和 .
分数可分为 和 .
整数
正整数
零
负整数
正分数
负分数
分数
负
有理
旧知回顾
(1分钟)
第二章 实数
1、体会生活中确实存在着不是有理数的数.
2、通过拼图活动,感受需要扩大数的范围的必要性。
3、会判断一个数是不是有理数,并会说明理由。
学习目标:(1分钟)
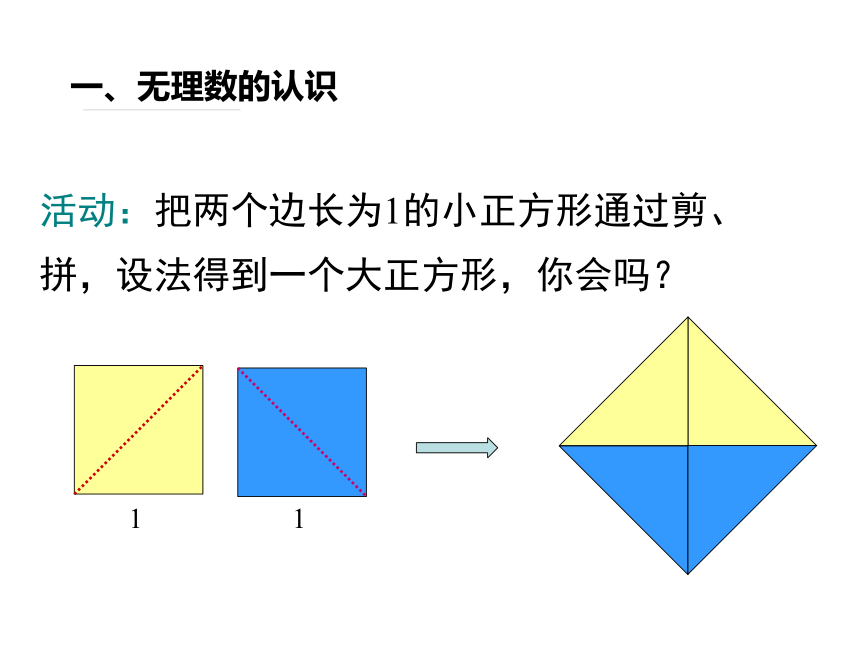
活动:把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形,你会吗?
1
1
1
一、无理数的认识
1
2
1
2
1
2
1
2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
还有好多方法哦!课余时间再动手试一试,比比谁找的多!
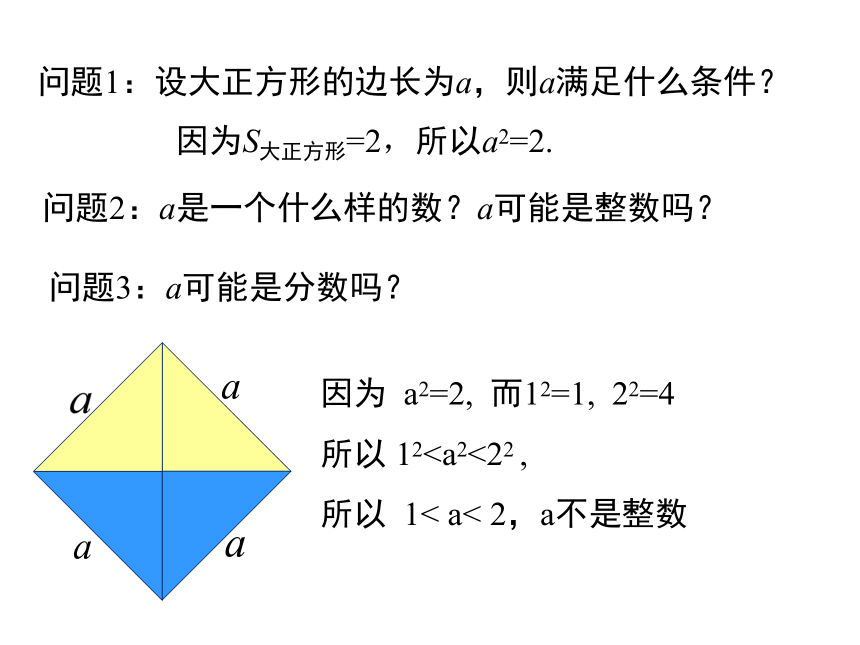
问题1:设大正方形的边长为a,则a满足什么条件?
问题2:a是一个什么样的数?a可能是整数吗?
因为S大正方形=2,所以a2=2.
因为 a2=2, 而12=1, 22=4
所以 12所以 1< a< 2,a不是整数
问题3:a可能是分数吗?
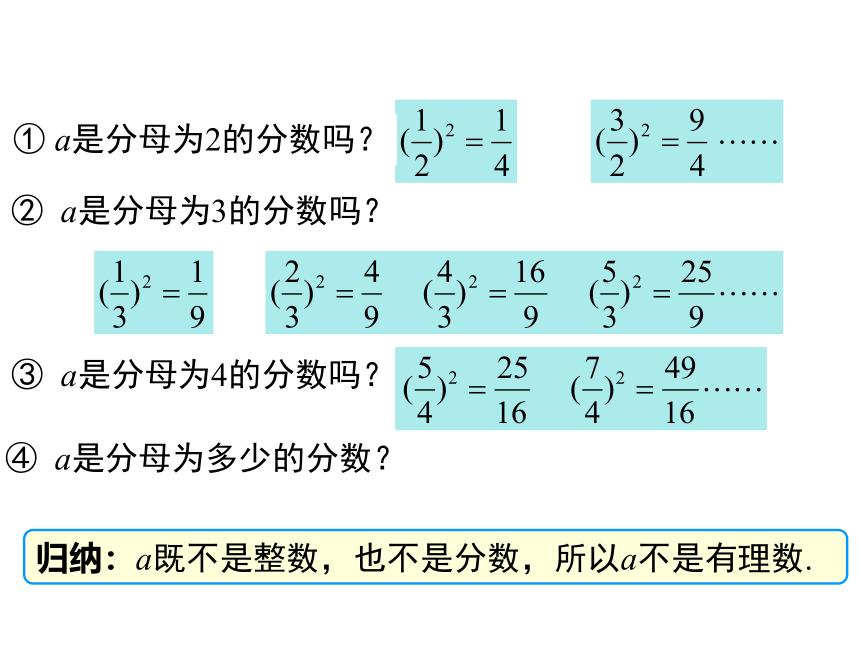
① a是分母为2的分数吗?
② a是分母为3的分数吗?
③ a是分母为4的分数吗?
④ a是分母为多少的分数?
归纳:a既不是整数,也不是分数,所以a不是有理数.
是有理数的线段有: 和
自学检测1:
1.若x2=8,则x是整数吗?是分数吗?是有理数吗?
2.在直角三角形ABC中,∠C=90°若a=2, b=3,
则c 满足什么条件?c是有理数吗?
x不是整数,不是分数,故不是有理数
必须满足:c2=a2+b2=22+32=13
c不是有理数
3.在右边正方形网格中,先找出长度为有理数的线段,再找出长度不是有理数的
线段.
=10
=5
AB
EF
不是有理数的线段有:
CD, GH, MN
2
1
A
B
C
E
F
b
自学指导2
1.自学课本P21做一做的内容,完成下列问题:
(1)如图,以直角三角形的斜边为边的正方形ABEF的面积是多少?
(2)设该正方形的边长为b,b满足什么条件?
(3)b是有理数吗?
2.有理数能完全满足我们的生活需要吗?
S正方形ABEF=AB×BE=b2=5
b2=AB2=AC2+BC2=22+12=5
b不是有理数
现实生活中,确实存在一种既不是整数,也不是分数的数,这种数一定不是有理数。如a2=2 b2=5,a, b都不是有理数。这说明有理数不能完全满足我们的生活需要。
学生自学,教师巡视(3分钟)
(1分钟)
3、(随堂练习P21):如图,等边三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?
自学检测2:(6分钟)
1、下面各正方形的边长不是有理数的是( )
(A)面积为25的正方形 (B)面积为16的正方形
(C)面积为7的正方形 (D)面积为1.44的正方形
C
2、若长方形的长、宽分别是3、4,那么它的对角线
的长是有理数吗?说明理由。
(变式)若长方形的长、宽分别是1、3,那么它的对角线的长是有理数吗?
是有理数,对角线的长等于5
不是有理数,对角线长的平方等于10
C
B
D
A
讨论﹑更正﹑点拨
(2分钟)
3、(随堂练习P21):如图,等边三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?
C
B
D
A
解:∵△ABC是等边三角形,AB=2且AD⊥BC
∴BD=DC= BC=1
则由勾股定理可得:h2=22-12=3
∴h不可能是整数,
也不可能是分数。
小结(2分钟)
1.通过拼图活动,感受在生活中确实存在既不是整数也不是分数的数,那么也不是有理数的数。
会确定一个数是有理数或不是有理数。
通过本课学习,大家都感受到有理数不够用了.请问你有什么收获与体会?
客观世界中,的确存在不是有理数的数,
除了本课所认识的非有理数的数以外,还有很多这样的数。例如:
m2=7,n2=11,k2=35 …其中m,n,k都不是有理数
当堂训练:(15分钟)
2.面积为6的长方形,长是宽的2倍,则宽为( )
A、小数 B、分数 C、不是有理数 D、不能确定
1
1
1
C
B
A
b
则b2=_____,b是整数吗?
3.如下图
5
和 之间。
3
2
,所以b值在整数
是分数吗?是有理数吗?为什么?
你能求出b的取值范围吗?
4、面积为13的正方形的边长m的值介于正整数 和
之间,m的值既不是 也不可能是 。
3
C
因为
1.直角边为1的等腰直角三角形的斜边c满足______,
它可以用整数或分数来表示吗?它是一个有理数吗?
c2=2
C不是有理数
c不能用整数或分数来表示
4
整数
分数
m不是有理数
5.如图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段.
6.长,宽分别是7,5的长方形,它的对角线的长c可能是整数吗?可能是分数吗?
(选做题)
解:∵由勾股定理得 c2=52+72=74
∴c既不是整数也不是分数.
至少找出两条长度是有理数的线段和两条长度不是有理数的线段(最长的和最短的).
A
B
C
D
E
F
两条有理数的线段:
最长的AC=5
最短的DE=1
两条不是有理数的线段:
最长的AB
最短的DF
P22问题解决2
正本作业
画在4×4的方格里
P22问题解决2,
(1)
(2)
(3)
板书设计
1.有理数:
2.不是有理数的数:
整数和分数
既不是整数也不是分数的数
a2=2,1a一定不是整数;
例如:
如右图
两个相同的最简分数的乘积仍然是分数,所以a不可能是分数。
现实生活中,确实存在一种既不是整数,也不是分数的数,
这种数一定不是有理数。
1.在初一我们学习了“数怎么不够用了”,从而引入了 数,进而把数的范围扩充到了 数.
2. 和 统称为有理数。
3.整数可分为 、 和 .
分数可分为 和 .
整数
正整数
零
负整数
正分数
负分数
分数
负
有理
旧知回顾
(1分钟)
第二章 实数
1、体会生活中确实存在着不是有理数的数.
2、通过拼图活动,感受需要扩大数的范围的必要性。
3、会判断一个数是不是有理数,并会说明理由。
学习目标:(1分钟)
活动:把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形,你会吗?
1
1
1
一、无理数的认识
1
2
1
2
1
2
1
2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
还有好多方法哦!课余时间再动手试一试,比比谁找的多!
问题1:设大正方形的边长为a,则a满足什么条件?
问题2:a是一个什么样的数?a可能是整数吗?
因为S大正方形=2,所以a2=2.
因为 a2=2, 而12=1, 22=4
所以 12
问题3:a可能是分数吗?
① a是分母为2的分数吗?
② a是分母为3的分数吗?
③ a是分母为4的分数吗?
④ a是分母为多少的分数?
归纳:a既不是整数,也不是分数,所以a不是有理数.
是有理数的线段有: 和
自学检测1:
1.若x2=8,则x是整数吗?是分数吗?是有理数吗?
2.在直角三角形ABC中,∠C=90°若a=2, b=3,
则c 满足什么条件?c是有理数吗?
x不是整数,不是分数,故不是有理数
必须满足:c2=a2+b2=22+32=13
c不是有理数
3.在右边正方形网格中,先找出长度为有理数的线段,再找出长度不是有理数的
线段.
=10
=5
AB
EF
不是有理数的线段有:
CD, GH, MN
2
1
A
B
C
E
F
b
自学指导2
1.自学课本P21做一做的内容,完成下列问题:
(1)如图,以直角三角形的斜边为边的正方形ABEF的面积是多少?
(2)设该正方形的边长为b,b满足什么条件?
(3)b是有理数吗?
2.有理数能完全满足我们的生活需要吗?
S正方形ABEF=AB×BE=b2=5
b2=AB2=AC2+BC2=22+12=5
b不是有理数
现实生活中,确实存在一种既不是整数,也不是分数的数,这种数一定不是有理数。如a2=2 b2=5,a, b都不是有理数。这说明有理数不能完全满足我们的生活需要。
学生自学,教师巡视(3分钟)
(1分钟)
3、(随堂练习P21):如图,等边三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?
自学检测2:(6分钟)
1、下面各正方形的边长不是有理数的是( )
(A)面积为25的正方形 (B)面积为16的正方形
(C)面积为7的正方形 (D)面积为1.44的正方形
C
2、若长方形的长、宽分别是3、4,那么它的对角线
的长是有理数吗?说明理由。
(变式)若长方形的长、宽分别是1、3,那么它的对角线的长是有理数吗?
是有理数,对角线的长等于5
不是有理数,对角线长的平方等于10
C
B
D
A
讨论﹑更正﹑点拨
(2分钟)
3、(随堂练习P21):如图,等边三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?
C
B
D
A
解:∵△ABC是等边三角形,AB=2且AD⊥BC
∴BD=DC= BC=1
则由勾股定理可得:h2=22-12=3
∴h不可能是整数,
也不可能是分数。
小结(2分钟)
1.通过拼图活动,感受在生活中确实存在既不是整数也不是分数的数,那么也不是有理数的数。
会确定一个数是有理数或不是有理数。
通过本课学习,大家都感受到有理数不够用了.请问你有什么收获与体会?
客观世界中,的确存在不是有理数的数,
除了本课所认识的非有理数的数以外,还有很多这样的数。例如:
m2=7,n2=11,k2=35 …其中m,n,k都不是有理数
当堂训练:(15分钟)
2.面积为6的长方形,长是宽的2倍,则宽为( )
A、小数 B、分数 C、不是有理数 D、不能确定
1
1
1
C
B
A
b
则b2=_____,b是整数吗?
3.如下图
5
和 之间。
3
2
,所以b值在整数
是分数吗?是有理数吗?为什么?
你能求出b的取值范围吗?
4、面积为13的正方形的边长m的值介于正整数 和
之间,m的值既不是 也不可能是 。
3
C
因为
1.直角边为1的等腰直角三角形的斜边c满足______,
它可以用整数或分数来表示吗?它是一个有理数吗?
c2=2
C不是有理数
c不能用整数或分数来表示
4
整数
分数
m不是有理数
5.如图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段.
6.长,宽分别是7,5的长方形,它的对角线的长c可能是整数吗?可能是分数吗?
(选做题)
解:∵由勾股定理得 c2=52+72=74
∴c既不是整数也不是分数.
至少找出两条长度是有理数的线段和两条长度不是有理数的线段(最长的和最短的).
A
B
C
D
E
F
两条有理数的线段:
最长的AC=5
最短的DE=1
两条不是有理数的线段:
最长的AB
最短的DF
P22问题解决2
正本作业
画在4×4的方格里
P22问题解决2,
(1)
(2)
(3)
板书设计
1.有理数:
2.不是有理数的数:
整数和分数
既不是整数也不是分数的数
a2=2,1
例如:
如右图
两个相同的最简分数的乘积仍然是分数,所以a不可能是分数。
现实生活中,确实存在一种既不是整数,也不是分数的数,
这种数一定不是有理数。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
