2.1认识无理数(2) 课件(共15张PPT)
文档属性
| 名称 | 2.1认识无理数(2) 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 204.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-11 21:34:40 | ||
图片预览





文档简介
(共15张PPT)
旧知回顾
(1分钟)
1.有理数的定义:
2.不是有理数的数有什么特征?举例说明
不是有理数的数:既不是整数也不是分数,例如:
a2=5 b2=8,其中a和b都不是有理数
整数和分数统称为有理数。
第二章 实数
学习目标 (1分钟)
1.理解并掌握无理数的定义,并会判断一个数是否是无理数。分清有理数与无理数的区别。
2.借助计算器,探索无理数是无限不循环小数。并会估算一个无理数的近似值。
(1)如图,三个正方形的边长之间有怎样的大小关系?
(2)a的整数部分是几?十分位是几?百分位呢?千分位呢?……完成下列表格
1
a
2
面积为2
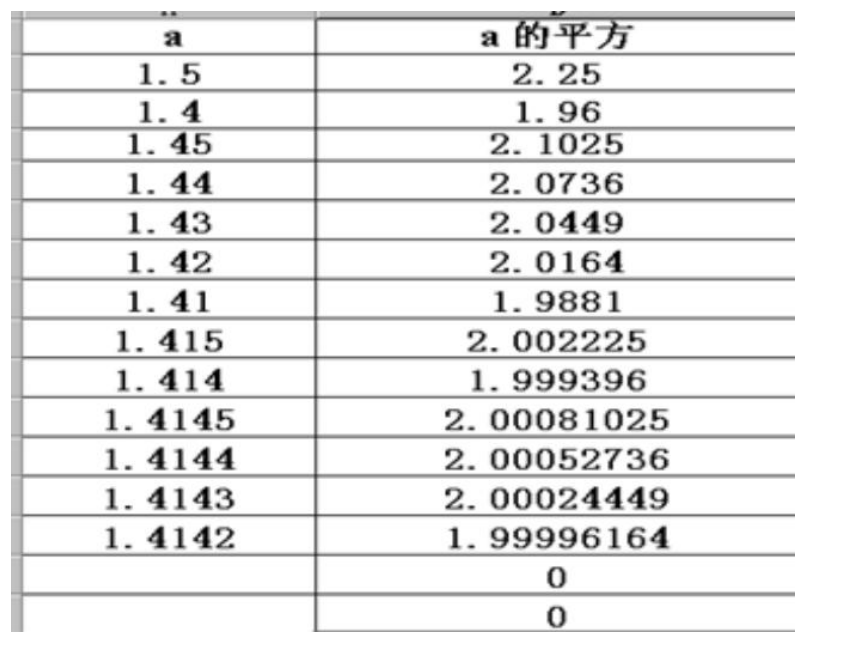
问题:上节课中a究竟是多少?
边长a 面积s
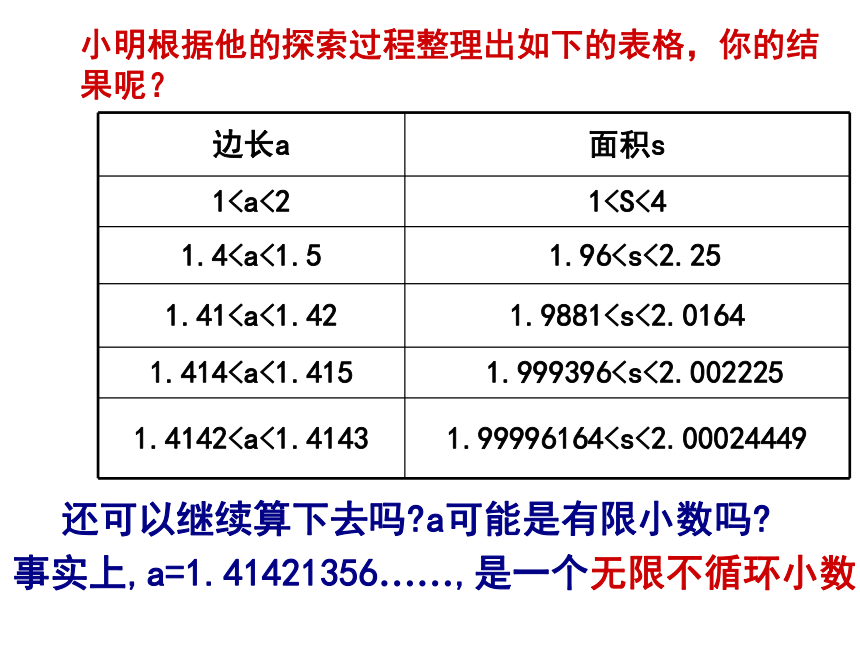
11.41.411.4141.4142还可以继续算下去吗 a可能是有限小数吗
事实上,a=1.41421356……,是一个无限不循环小数
小明根据他的探索过程整理出如下的表格,你的结果呢?
估计面积为5的正方形的边长b的值,结果精确到百分位.
b=2.236067978…,它也是一个无限不循环小数
做一做
2、像0.585885888588885…,
1.41421356…,2.2360679…等这些数的小数位数都是
无限的,但是又不是循环的,是无限不循环小数
. 叫做无理数(圆周率π=3.14159265…
也是一个无限不循环小数,故π是无理数)
自学课本P23 “议一议”,完成下列问题:
1、把下列各数表示成小数,你发现什么?
无限不循环小数
有理数总可以用有限小数或无限循环小数表示。
反过来,任何有限小数或无限循环小数也都是有理数。
0.8
.
0.5
0.17
.
-
0.1 8
..
学生自学,教师巡视(4分钟)
0.4583,3.7,- ,18 , ,
3.97,-234.10101010……
0.12345678910111213……
(小数部分由相继的正整数组成)
A.面积为25的正方形 B.面积为 的正方形
C.面积为8的正方形 D.面积为1.44的正方形
C
以下各正方形的边长是无理数的是( )
3.
√
1.下列各数中,哪些是有理数(√) 哪些是无理数?
√
√
√
√
√
√
,
自学检测2(6分钟)
2.请写出一个大于3而小于4的无理数 。
如π,3.01001000100001…
易错点: 是分数吗?
4、下列说法中,正确的是( )
A.所有无限小数都是无理数
B.所有无理数都是无限小数
C.有理数都是有限小数
D.不是无限小数的不是无理数
B
5、如果x2=10,则x是一个 数 ,x的整数部分是 。
无理
3
1、_________________叫无理数。
2、常见的无理数有哪些形式?
无限不循环小数
(1)含π型
(2)构造型
例如:-3π,2π,
例如:0.10100100010000‥‥‥
小结(2分钟)
3.数的分类
(按小数的形式来分)
有理数:有限小数或无限循环小数
无理数:无限不循环小数
实数
整数
分数
注意:.无限小数包括无限循环小数和无限不循环小数,
其中,无限循环小数是有理数,无限不循环小数是无理数
(3)开方开不尽的根式型
例如:
1、下列各数中,哪些是无理数(√)?哪些是有理数?
0.123432123432 …,3.14, , 0.57,
0.101001000100001, , ,
1.2332333233332…,
当堂训练
.
.
√
√
√
√
(15分钟)
2、面积是25的正方形的边长为 ,它是 数。
面积为7 的正方形边长a的整数部分是 ,
边长a是一个 数
3、已知a、b是两个连续正整数,且a2﹤7﹤b2,
则a+b=____
5
有理
2
无理
5
解:∵∠C=900,
∴,由勾股定理得,C2=a2+b2=22+32=13
∵32<13 <42
∴ 3.62 =12.96
3.652=13.3225
∴c≈3.6
(选做题)
1.已知m2=26,n2=88,那么在m、n之间的正整数有________ .
6, 7, 8, 9
4、在直角三角形ABC中,∠C=90°若a=2,b=3,
则c满足什么条件?C是有理数吗?你能确定c的近
似值吗?(精确到0.1)
P25 T2,T3
正本作业
2.(1)设面积为20的正方形的边长为x,x是有理数吗?说说你的理由.
(2)估计x的值(结果精确到0.1),并用计算器验证你的估计。
(3)如果结果精确到0.01呢?
x2=20,16是整数,故x不是有理数.
x一定不是整数;
x ≈4.5 (
∵ 4.42 =19.36, 4.52=20.25)
x ≈4.47
4.482 =20.0704, 4.472=19.9809)
(∵
T2.(1)设面积为10的正方形的边长为x,x是有理数吗?说说你的理由.
(2)估计x的值(结果精确到0.1),并用计算器验证你的估计。
(3)如果结果精确到0.01呢?
x2=10,9是整数,故x不是有理数.
x一定不是整数;
x ≈3.2 (
∵ 3.12=9.61, 3.152 =9.9225,3.22=10.24)
x ≈3.16
3.1612 =9.991921, 3.1622=9.998244,
3.1632=10.004569 )
(∵
T3 (1) ×(2) √(3) ×(4) ×
1、_________________叫无理数。
2、常见的无理数有哪些形式?
无限不循环小数
(1)含π型
例如:-3π,2π,
(2)构造型
例如:0.10100100010000‥‥‥
3.数的分类
(按小数的形式来分)
有理数:有限小数或无限循环小数
无理数:无限不循环小数
实数
整数
分数
注意:.无限小数包括无限循环小数和无限不循环小数,
其中,无限循环小数是有理数,无限不循环小数是无理数
板书设计
旧知回顾
(1分钟)
1.有理数的定义:
2.不是有理数的数有什么特征?举例说明
不是有理数的数:既不是整数也不是分数,例如:
a2=5 b2=8,其中a和b都不是有理数
整数和分数统称为有理数。
第二章 实数
学习目标 (1分钟)
1.理解并掌握无理数的定义,并会判断一个数是否是无理数。分清有理数与无理数的区别。
2.借助计算器,探索无理数是无限不循环小数。并会估算一个无理数的近似值。
(1)如图,三个正方形的边长之间有怎样的大小关系?
(2)a的整数部分是几?十分位是几?百分位呢?千分位呢?……完成下列表格
1
a
2
面积为2
问题:上节课中a究竟是多少?
边长a 面积s
1
事实上,a=1.41421356……,是一个无限不循环小数
小明根据他的探索过程整理出如下的表格,你的结果呢?
估计面积为5的正方形的边长b的值,结果精确到百分位.
b=2.236067978…,它也是一个无限不循环小数
做一做
2、像0.585885888588885…,
1.41421356…,2.2360679…等这些数的小数位数都是
无限的,但是又不是循环的,是无限不循环小数
. 叫做无理数(圆周率π=3.14159265…
也是一个无限不循环小数,故π是无理数)
自学课本P23 “议一议”,完成下列问题:
1、把下列各数表示成小数,你发现什么?
无限不循环小数
有理数总可以用有限小数或无限循环小数表示。
反过来,任何有限小数或无限循环小数也都是有理数。
0.8
.
0.5
0.17
.
-
0.1 8
..
学生自学,教师巡视(4分钟)
0.4583,3.7,- ,18 , ,
3.97,-234.10101010……
0.12345678910111213……
(小数部分由相继的正整数组成)
A.面积为25的正方形 B.面积为 的正方形
C.面积为8的正方形 D.面积为1.44的正方形
C
以下各正方形的边长是无理数的是( )
3.
√
1.下列各数中,哪些是有理数(√) 哪些是无理数?
√
√
√
√
√
√
,
自学检测2(6分钟)
2.请写出一个大于3而小于4的无理数 。
如π,3.01001000100001…
易错点: 是分数吗?
4、下列说法中,正确的是( )
A.所有无限小数都是无理数
B.所有无理数都是无限小数
C.有理数都是有限小数
D.不是无限小数的不是无理数
B
5、如果x2=10,则x是一个 数 ,x的整数部分是 。
无理
3
1、_________________叫无理数。
2、常见的无理数有哪些形式?
无限不循环小数
(1)含π型
(2)构造型
例如:-3π,2π,
例如:0.10100100010000‥‥‥
小结(2分钟)
3.数的分类
(按小数的形式来分)
有理数:有限小数或无限循环小数
无理数:无限不循环小数
实数
整数
分数
注意:.无限小数包括无限循环小数和无限不循环小数,
其中,无限循环小数是有理数,无限不循环小数是无理数
(3)开方开不尽的根式型
例如:
1、下列各数中,哪些是无理数(√)?哪些是有理数?
0.123432123432 …,3.14, , 0.57,
0.101001000100001, , ,
1.2332333233332…,
当堂训练
.
.
√
√
√
√
(15分钟)
2、面积是25的正方形的边长为 ,它是 数。
面积为7 的正方形边长a的整数部分是 ,
边长a是一个 数
3、已知a、b是两个连续正整数,且a2﹤7﹤b2,
则a+b=____
5
有理
2
无理
5
解:∵∠C=900,
∴,由勾股定理得,C2=a2+b2=22+32=13
∵32<13 <42
∴ 3.62 =12.96
3.652=13.3225
∴c≈3.6
(选做题)
1.已知m2=26,n2=88,那么在m、n之间的正整数有________ .
6, 7, 8, 9
4、在直角三角形ABC中,∠C=90°若a=2,b=3,
则c满足什么条件?C是有理数吗?你能确定c的近
似值吗?(精确到0.1)
P25 T2,T3
正本作业
2.(1)设面积为20的正方形的边长为x,x是有理数吗?说说你的理由.
(2)估计x的值(结果精确到0.1),并用计算器验证你的估计。
(3)如果结果精确到0.01呢?
x2=20,16
x一定不是整数;
x ≈4.5 (
∵ 4.42 =19.36, 4.52=20.25)
x ≈4.47
4.482 =20.0704, 4.472=19.9809)
(∵
T2.(1)设面积为10的正方形的边长为x,x是有理数吗?说说你的理由.
(2)估计x的值(结果精确到0.1),并用计算器验证你的估计。
(3)如果结果精确到0.01呢?
x2=10,9
x一定不是整数;
x ≈3.2 (
∵ 3.12=9.61, 3.152 =9.9225,3.22=10.24)
x ≈3.16
3.1612 =9.991921, 3.1622=9.998244,
3.1632=10.004569 )
(∵
T3 (1) ×(2) √(3) ×(4) ×
1、_________________叫无理数。
2、常见的无理数有哪些形式?
无限不循环小数
(1)含π型
例如:-3π,2π,
(2)构造型
例如:0.10100100010000‥‥‥
3.数的分类
(按小数的形式来分)
有理数:有限小数或无限循环小数
无理数:无限不循环小数
实数
整数
分数
注意:.无限小数包括无限循环小数和无限不循环小数,
其中,无限循环小数是有理数,无限不循环小数是无理数
板书设计
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
