第四章 几何图形初步测试题(含答案)
图片预览

文档简介
第四章 几何图形初步测试题
一、选择题(本大题共10小题,每小题3分,共30分)
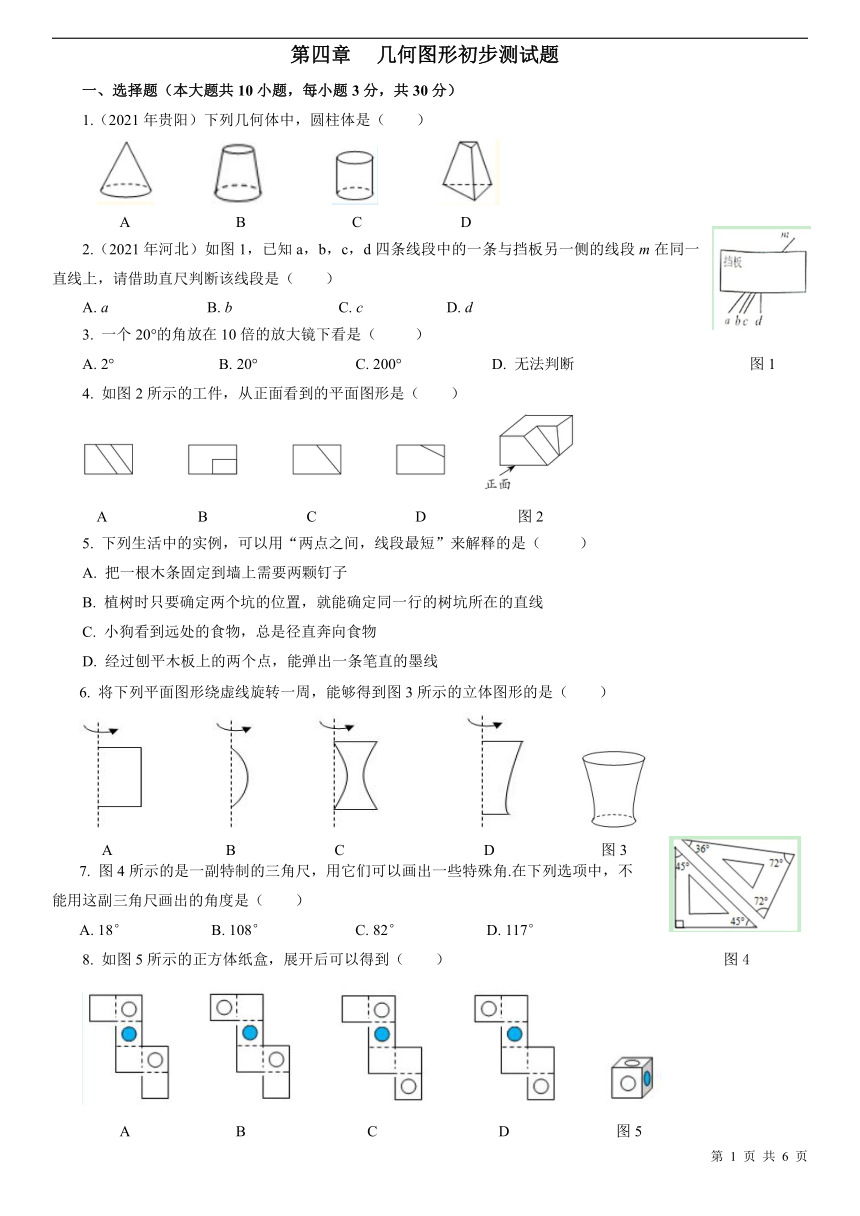
1.(2021年贵阳)下列几何体中,圆柱体是( )
A B C D
2.(2021年河北)如图1,已知a,b,c,d四条线段中的一条与挡板另一侧的线段m在同一直线上,请借助直尺判断该线段是( )
A. a B. b C. c D. d
3. 一个20°的角放在10倍的放大镜下看是( )
A. 2° B. 20° C. 200° D. 无法判断 图1
4. 如图2所示的工件,从正面看到的平面图形是( )
A B C D 图2
5. 下列生活中的实例,可以用“两点之间,线段最短”来解释的是( )
A. 把一根木条固定到墙上需要两颗钉子
B. 植树时只要确定两个坑的位置,就能确定同一行的树坑所在的直线
C. 小狗看到远处的食物,总是径直奔向食物
D. 经过刨平木板上的两个点,能弹出一条笔直的墨线
6. 将下列平面图形绕虚线旋转一周,能够得到图3所示的立体图形的是( )
A B C D 图3
7. 图4所示的是一副特制的三角尺,用它们可以画出一些特殊角.在下列选项中,不
能用这副三角尺画出的角度是( )
A. 18° B. 108° C. 82° D. 117°
8. 如图5所示的正方体纸盒,展开后可以得到( ) 图4
A B C D 图5
第 4 页 共 6 页
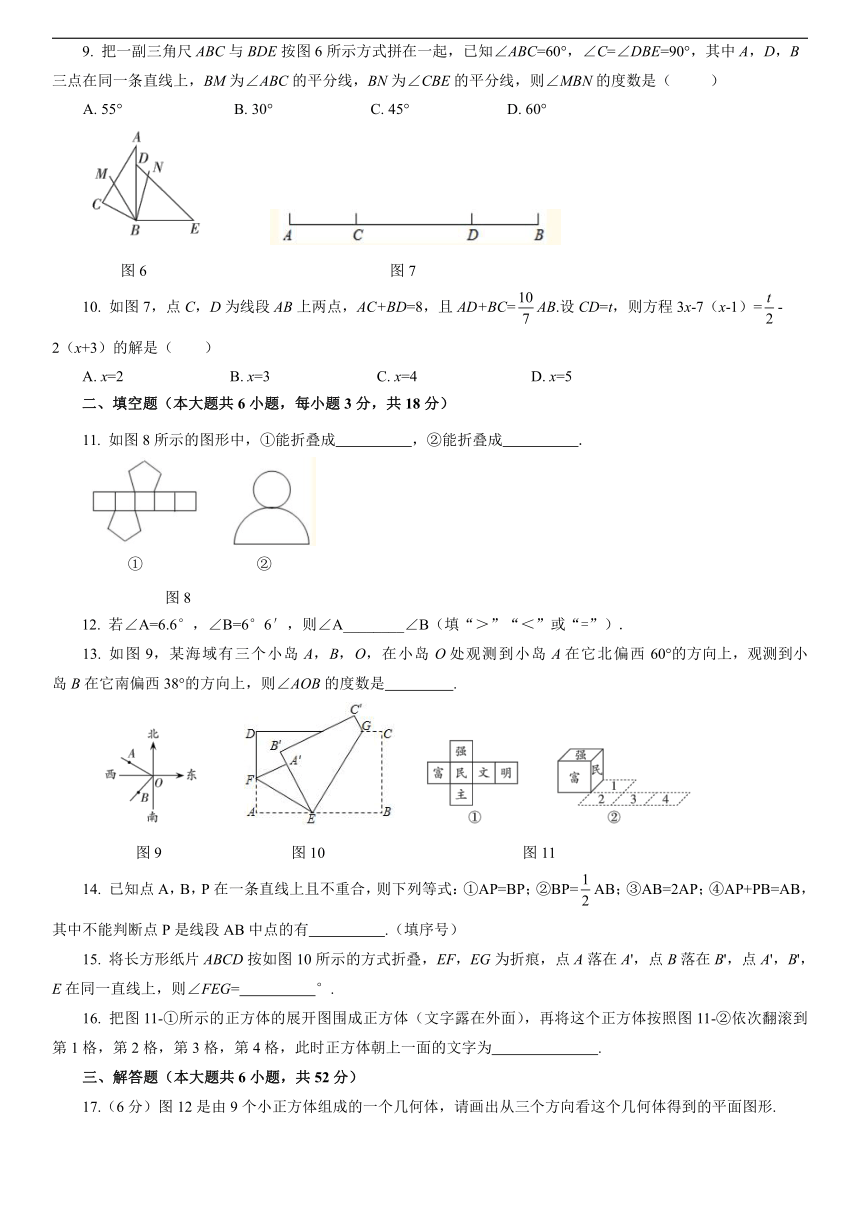
9. 把一副三角尺ABC与BDE按图6所示方式拼在一起,已知∠ABC=60°,∠C=∠DBE=90°,其中A,D,B
三点在同一条直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )
A. 55° B. 30° C. 45° D. 60°
图6 图7
10. 如图7,点C,D为线段AB上两点,AC+BD=8,且AD+BC=AB.设CD=t,则方程3x-7(x-1)=-
2(x+3)的解是( )
A. x=2 B. x=3 C. x=4 D. x=5
二、填空题(本大题共6小题,每小题3分,共18分)
11. 如图8所示的图形中,①能折叠成 ,②能折叠成 .
① ②
图8
12. 若∠A=6.6°,∠B=6°6′,则∠A________∠B(填“>”“<”或“=”).
13. 如图9,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏西60°的方向上,观测到小
岛B在它南偏西38°的方向上,则∠AOB的度数是 .
图9 图10 图11
14. 已知点A,B,P在一条直线上且不重合,则下列等式:①AP=BP;②BP=AB;③AB=2AP;④AP+PB=AB,其中不能判断点P是线段AB中点的有 .(填序号)
15. 将长方形纸片ABCD按如图10所示的方式折叠,EF,EG为折痕,点A落在A',点B落在B',点A',B',E在同一直线上,则∠FEG= °.
16. 把图11-①所示的正方体的展开图围成正方体(文字露在外面),再将这个正方体按照图11-②依次翻滚到第1格,第2格,第3格,第4格,此时正方体朝上一面的文字为 .
三、解答题(本大题共6小题,共52分)
17.(6分)图12是由9个小正方体组成的一个几何体,请画出从三个方向看这个几何体得到的平面图形.
图12
18.(8分)如图13,已知AB=2,延长线段AB至点C,使BC=2AB,点D是线段AC的中点,用刻度尺画出图形,并求线段BD的长度.
图13
19.(8分)已知∠α=76°,∠β=41°31′,求:
(1)∠β的余角;
(2)∠α的2倍与∠β的的差.
20.(8分)如图14,C为线段AB的中点,E为线段AB上的点,D为线段AE的中点.
(1)若线段AB=a,CE=b,且(a-15)2+∣2b-9∣=0,求a,b的值;
(2)在(1)的条件下,求线段CD的长.
图14
21.(10分)聪聪在学习了“展开与折叠”这部分内容后,明白了很多几何体都能展开成平面图形,于是他在
家用剪刀把一个长方体纸盒(如图15-(1))剪开了,可是他一不小心多剪了一条棱,把纸盒剪成了两部分,即图15-(2)中的①和②.根据你所学的知识,回答下列问题:
(1)若这个长方体纸盒的长、宽、高分别是8 cm,4 cm,2 cm,则该长方体纸盒的体积是多少?
(2)聪聪一共剪开了____________条棱;
(3)现在聪聪想将剪掉的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为
他应该将剪掉的②粘贴到①中的什么位置?请你帮助他在①上补全一种情况.
图15
22.(12分)已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1)如图16-①,当∠BOC=40°时,求∠DOE的度数;
(2)如图16-②,当射线OC在∠AOB内绕O点旋转时,OD,OE始终分别是∠AOC与∠BOC的平分线,则
∠DOE的大小是否发生变化?说明理由;
(3)当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时,OD,OE仍始终是∠AOC与∠BOC的平分线,直
接写出∠DOE的度数(不必写过程).
① ②
图16
附加题(共20分,不计入总分)
1.(6分)图1是从正面、左面、上面看由一些相同的小正方体搭成的几何体得到的平面图形,则搭成这个几何
体的小正方体的个数是( )
A. 4 B. 5 C. 6 D. 7
图1
2.(14分)已知A,B两点在数轴上的位置如图2所示,其中点A表示的有理数为-4,且AB=10.点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t(t>0)秒.
(1)当t=1时,线段AP的长为 ,点P表示的有理数为 ;
(2)当PB=2时,求t的值;
(3)若M为线段AP的中点,N为线段PB的中点,在点P运动的过程中,线段MN的长度是否发生变化?若发生变化,请说明理由;若不发生变化,求出线段MN的长.
图2
(吉林 刘春霞)
第四章 几何图形初步测试题参考答案
一、1. C 2. A 3. B 4. C 5. C 6. D 7. C 8. A 9. C
10. D 提示:因为AD+BC=AB=AC+CD+BD+CD,AC+BD=8,AB=AC+BD+CD,所以(8+CD)=2CD+8,解得CD=6,即t=6.所以方程3x-7(x-1)=3-2(x+3)的解为x=5.
二、11. 五棱柱 圆锥 12. > 13. 82° 14. ②③④ 15. 90 16. 富
三、17. 解:(1)如图1所示.
图1
18. 解:如图2所示.
图2
由BC=2AB,AB=2,得BC=4,所以AC=AB+BC=2+4=6.
因为点D是线段AC的中点,所以AD=AC=×6=3.
所以BD=AD-AB=3-2=1.
19. 解:(1)90°-∠β=90°-41°31′=48°29′;
(2)2∠α-∠β=2×76°-×41°31′=152°-20°45′30″=131°14′30″.
20. 解:(1)由(a-15)2+∣2b-9∣=0,得a-15=0,2b-9=0.解得a=15,b=4.5.
(2)因为C为线段AB的中点,AB=15,CE=4.5,所以AC=7.5,所以AE=AC+CE=7.5+4.5=12.
因为D为线段AE的中点,所以DE=AE=×12=6,所以CD=DE CE=6-4.5=1.5.
21. 解:(1)该长方体纸盒的体积是:8×4×2=64(cm3);
(2)8
(3)答案不唯一,有以下三种情况供参考,如图3.
图3
22. 解:(1)∠AOC=90°-∠BOC=50°.
因为OD,OE分别平分∠AOC和∠BOC,所以∠COD=∠AOC=25°,∠COE= QUOTE ∠BOC=20°.
所以∠DOE=∠COD+∠COE=45°.
(2)∠DOE的大小不变.
理由是:∠DOE=∠COD+∠COE= QUOTE ∠AOC+ QUOTE ∠BOC= QUOTE (∠AOC+∠BOC)= QUOTE ∠AOB=45°.
(3)∠DOE=45°或135°.
提示:分两种情况:如答图①,∠DOE=45°;如答图②,∠DOE=135°.
① ②
附加题
1. B 提示:由从正面看和从上面看可知,几何体的底层有3个小正方体;由从正面看和从左面看可知,几何
体的第二层有2个小正方体.则搭成这个几何体的小正方体的个数为3+2=5.
2. 解:(1)2 -2
(2)当点P在点B左侧时,因为AB=10,AP=2t,所以PB=10-2t.
由题意,得10-2t=2,解得t=4.
当点P在点B右侧时,因为AB=10,AP=2t,所以PB=2t-10.
由题意,得2t-10=2,解得t=6.
综上,t=4或t=6.
(3)如图1,当点P在线段AB上时,MN=MP+PN=AP+PB=(AP+PB)=AB=×10=5;
如图2,当点P在AB延长线上时,MN=MP-NP=AP-PB=(AP-PB)=AB=×10=5.
综上,线段MN的长度不发生变化,其值为5.
一、选择题(本大题共10小题,每小题3分,共30分)
1.(2021年贵阳)下列几何体中,圆柱体是( )
A B C D
2.(2021年河北)如图1,已知a,b,c,d四条线段中的一条与挡板另一侧的线段m在同一直线上,请借助直尺判断该线段是( )
A. a B. b C. c D. d
3. 一个20°的角放在10倍的放大镜下看是( )
A. 2° B. 20° C. 200° D. 无法判断 图1
4. 如图2所示的工件,从正面看到的平面图形是( )
A B C D 图2
5. 下列生活中的实例,可以用“两点之间,线段最短”来解释的是( )
A. 把一根木条固定到墙上需要两颗钉子
B. 植树时只要确定两个坑的位置,就能确定同一行的树坑所在的直线
C. 小狗看到远处的食物,总是径直奔向食物
D. 经过刨平木板上的两个点,能弹出一条笔直的墨线
6. 将下列平面图形绕虚线旋转一周,能够得到图3所示的立体图形的是( )
A B C D 图3
7. 图4所示的是一副特制的三角尺,用它们可以画出一些特殊角.在下列选项中,不
能用这副三角尺画出的角度是( )
A. 18° B. 108° C. 82° D. 117°
8. 如图5所示的正方体纸盒,展开后可以得到( ) 图4
A B C D 图5
第 4 页 共 6 页
9. 把一副三角尺ABC与BDE按图6所示方式拼在一起,已知∠ABC=60°,∠C=∠DBE=90°,其中A,D,B
三点在同一条直线上,BM为∠ABC的平分线,BN为∠CBE的平分线,则∠MBN的度数是( )
A. 55° B. 30° C. 45° D. 60°
图6 图7
10. 如图7,点C,D为线段AB上两点,AC+BD=8,且AD+BC=AB.设CD=t,则方程3x-7(x-1)=-
2(x+3)的解是( )
A. x=2 B. x=3 C. x=4 D. x=5
二、填空题(本大题共6小题,每小题3分,共18分)
11. 如图8所示的图形中,①能折叠成 ,②能折叠成 .
① ②
图8
12. 若∠A=6.6°,∠B=6°6′,则∠A________∠B(填“>”“<”或“=”).
13. 如图9,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏西60°的方向上,观测到小
岛B在它南偏西38°的方向上,则∠AOB的度数是 .
图9 图10 图11
14. 已知点A,B,P在一条直线上且不重合,则下列等式:①AP=BP;②BP=AB;③AB=2AP;④AP+PB=AB,其中不能判断点P是线段AB中点的有 .(填序号)
15. 将长方形纸片ABCD按如图10所示的方式折叠,EF,EG为折痕,点A落在A',点B落在B',点A',B',E在同一直线上,则∠FEG= °.
16. 把图11-①所示的正方体的展开图围成正方体(文字露在外面),再将这个正方体按照图11-②依次翻滚到第1格,第2格,第3格,第4格,此时正方体朝上一面的文字为 .
三、解答题(本大题共6小题,共52分)
17.(6分)图12是由9个小正方体组成的一个几何体,请画出从三个方向看这个几何体得到的平面图形.
图12
18.(8分)如图13,已知AB=2,延长线段AB至点C,使BC=2AB,点D是线段AC的中点,用刻度尺画出图形,并求线段BD的长度.
图13
19.(8分)已知∠α=76°,∠β=41°31′,求:
(1)∠β的余角;
(2)∠α的2倍与∠β的的差.
20.(8分)如图14,C为线段AB的中点,E为线段AB上的点,D为线段AE的中点.
(1)若线段AB=a,CE=b,且(a-15)2+∣2b-9∣=0,求a,b的值;
(2)在(1)的条件下,求线段CD的长.
图14
21.(10分)聪聪在学习了“展开与折叠”这部分内容后,明白了很多几何体都能展开成平面图形,于是他在
家用剪刀把一个长方体纸盒(如图15-(1))剪开了,可是他一不小心多剪了一条棱,把纸盒剪成了两部分,即图15-(2)中的①和②.根据你所学的知识,回答下列问题:
(1)若这个长方体纸盒的长、宽、高分别是8 cm,4 cm,2 cm,则该长方体纸盒的体积是多少?
(2)聪聪一共剪开了____________条棱;
(3)现在聪聪想将剪掉的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为
他应该将剪掉的②粘贴到①中的什么位置?请你帮助他在①上补全一种情况.
图15
22.(12分)已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
(1)如图16-①,当∠BOC=40°时,求∠DOE的度数;
(2)如图16-②,当射线OC在∠AOB内绕O点旋转时,OD,OE始终分别是∠AOC与∠BOC的平分线,则
∠DOE的大小是否发生变化?说明理由;
(3)当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时,OD,OE仍始终是∠AOC与∠BOC的平分线,直
接写出∠DOE的度数(不必写过程).
① ②
图16
附加题(共20分,不计入总分)
1.(6分)图1是从正面、左面、上面看由一些相同的小正方体搭成的几何体得到的平面图形,则搭成这个几何
体的小正方体的个数是( )
A. 4 B. 5 C. 6 D. 7
图1
2.(14分)已知A,B两点在数轴上的位置如图2所示,其中点A表示的有理数为-4,且AB=10.点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t(t>0)秒.
(1)当t=1时,线段AP的长为 ,点P表示的有理数为 ;
(2)当PB=2时,求t的值;
(3)若M为线段AP的中点,N为线段PB的中点,在点P运动的过程中,线段MN的长度是否发生变化?若发生变化,请说明理由;若不发生变化,求出线段MN的长.
图2
(吉林 刘春霞)
第四章 几何图形初步测试题参考答案
一、1. C 2. A 3. B 4. C 5. C 6. D 7. C 8. A 9. C
10. D 提示:因为AD+BC=AB=AC+CD+BD+CD,AC+BD=8,AB=AC+BD+CD,所以(8+CD)=2CD+8,解得CD=6,即t=6.所以方程3x-7(x-1)=3-2(x+3)的解为x=5.
二、11. 五棱柱 圆锥 12. > 13. 82° 14. ②③④ 15. 90 16. 富
三、17. 解:(1)如图1所示.
图1
18. 解:如图2所示.
图2
由BC=2AB,AB=2,得BC=4,所以AC=AB+BC=2+4=6.
因为点D是线段AC的中点,所以AD=AC=×6=3.
所以BD=AD-AB=3-2=1.
19. 解:(1)90°-∠β=90°-41°31′=48°29′;
(2)2∠α-∠β=2×76°-×41°31′=152°-20°45′30″=131°14′30″.
20. 解:(1)由(a-15)2+∣2b-9∣=0,得a-15=0,2b-9=0.解得a=15,b=4.5.
(2)因为C为线段AB的中点,AB=15,CE=4.5,所以AC=7.5,所以AE=AC+CE=7.5+4.5=12.
因为D为线段AE的中点,所以DE=AE=×12=6,所以CD=DE CE=6-4.5=1.5.
21. 解:(1)该长方体纸盒的体积是:8×4×2=64(cm3);
(2)8
(3)答案不唯一,有以下三种情况供参考,如图3.
图3
22. 解:(1)∠AOC=90°-∠BOC=50°.
因为OD,OE分别平分∠AOC和∠BOC,所以∠COD=∠AOC=25°,∠COE= QUOTE ∠BOC=20°.
所以∠DOE=∠COD+∠COE=45°.
(2)∠DOE的大小不变.
理由是:∠DOE=∠COD+∠COE= QUOTE ∠AOC+ QUOTE ∠BOC= QUOTE (∠AOC+∠BOC)= QUOTE ∠AOB=45°.
(3)∠DOE=45°或135°.
提示:分两种情况:如答图①,∠DOE=45°;如答图②,∠DOE=135°.
① ②
附加题
1. B 提示:由从正面看和从上面看可知,几何体的底层有3个小正方体;由从正面看和从左面看可知,几何
体的第二层有2个小正方体.则搭成这个几何体的小正方体的个数为3+2=5.
2. 解:(1)2 -2
(2)当点P在点B左侧时,因为AB=10,AP=2t,所以PB=10-2t.
由题意,得10-2t=2,解得t=4.
当点P在点B右侧时,因为AB=10,AP=2t,所以PB=2t-10.
由题意,得2t-10=2,解得t=6.
综上,t=4或t=6.
(3)如图1,当点P在线段AB上时,MN=MP+PN=AP+PB=(AP+PB)=AB=×10=5;
如图2,当点P在AB延长线上时,MN=MP-NP=AP-PB=(AP-PB)=AB=×10=5.
综上,线段MN的长度不发生变化,其值为5.
