6.1函数 同步练习(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章 一次函数
1 函数
基础过关
知识点1 函数的概念
1.2021年春节期间,疫情形势复杂,王丽遵循“防疫当前,本地过年”的原则,给远在家乡的亲人打电话拜年.电话费随着通话时间的变化而变化,在这个过程中,因变量是( )
A.王丽 B.电话费 C.通话时间 D.亲人
2.刘师傅到加油站加油,如图是所用的加油机上某一时刻的数据显示牌,则其中的变量是( )
A.金额 B.单价 C.数量 D.金额和数量
3.下列所描述的四个变化过程中,变量之间的关系不能看成函数关系的是( )
A.三角形的一个外角的度数x度和与它相邻的内角的度数y度的关系
B.树的高度为60厘米,每个月长高3厘米,x个月后,树的高度为y厘米,x与y的关系
C.正方形的面积y(平方厘米)和它的边长x(厘米)的关系
D.y是正数x的平方根,y与x之间的关系
4.若y=x ,则y________x的函数,x__________y的函数.(填“是”或“不是”)
知识点2 函数的表示方法
5.如图是某市一天的气温随时间变化的情况,下列说法正确的是( )
A.这一天的最低气温是-4℃ B.这一天12时的气温最高
C.最高气温比最低气温高8℃ D.0时至8时的气温呈下降趋势
6.用固定的速度往如图所示的杯子里注水,用x表示注水时间,y表示水杯底部到水面的高度,下列图象能大致表示y与x之间的关系的是( )
7.变量x,y的一些对应值如表:
x … -2 -1 0 1 2 3 …
y … 4 2 0 -2 -4 -6 …
根据表格中的数据规律,当x=11时,y的值是( )
A.-22 B.-11 C.11 D.22
8.如图①,在Rt△ABC中,∠BAC=90°,点P从点A出发,沿三角形的边以1cm/s的速度逆时针运动一周,图②是点P运动时,线段AP的长度y(cm)随运动时间x(s)变化的图象,其中Q是曲线部分的最低点,则点Q的坐标是_____________.
9.七年级二班制作文化墙时制作花边,需要将数张长为20cm,宽为8cm的长方形卡纸按如图所示的方式粘合起来,粘合部分的宽为3cm.
(1)根据题意,将下面的表格补充完整;
卡纸张数x(张) 1 2 3 4 5 …
纸条长度y(cm) 20 ____ 54 71 ____ …
(2)直接写出用x表示y的关系式:__________________;
(3)要使粘合后的总长度为1006cm,需用多少张这样的卡纸
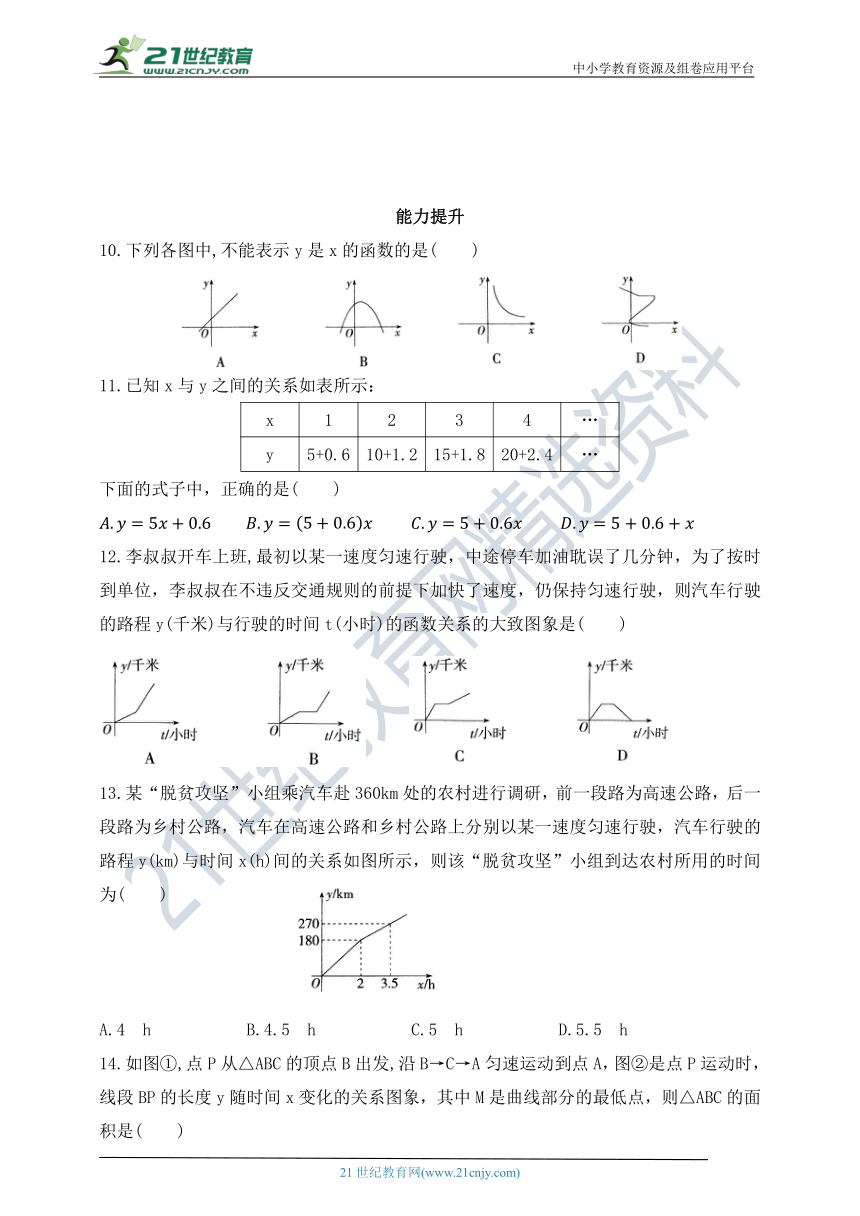
能力提升
10.下列各图中,不能表示y是x的函数的是( )
11.已知x与y之间的关系如表所示:
x 1 2 3 4 …
y 5+0.6 10+1.2 15+1.8 20+2.4 …
下面的式子中,正确的是( )
12.李叔叔开车上班,最初以某一速度匀速行驶,中途停车加油耽误了几分钟,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,仍保持匀速行驶,则汽车行驶的路程y(千米)与行驶的时间t(小时)的函数关系的大致图象是( )
13.某“脱贫攻坚”小组乘汽车赴360km处的农村进行调研,前一段路为高速公路,后一段路为乡村公路,汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(km)与时间x(h)间的关系如图所示,则该“脱贫攻坚”小组到达农村所用的时间为( )
A.4 h B.4.5 h C.5 h D.5.5 h
14.如图①,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图②是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M是曲线部分的最低点,则△ABC的面积是( )
A.12 B.24 C.36 D.48
15.在登山过程中,海拔每升高1千米,气温下降6℃,已知某登山大本营所在的位置的气温是2℃,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是y℃,那么y关于x的函数表达式是_________________.
16.如图是一个运算程序示意图,若开始输入x的值为3,则输出y的值为__________.
17.[应用意识]实验证实,放射性物质在放出射线后,质量将减少,减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某种函数关系.
如图为表示镭的放射规律的函数图象,据此,32mg镭缩减为1mg所用的时间大约是( )
A.4860年 B.6480年 C.8100年 D.9720年
18.[几何直观]如图,从第一个三角形到第n个三角形,每个三角形中的三个数之间均具有相同的规律,按此规律,第n个三角形中,y与n之间的关系式是______________.
参考答案
基础过关
1.B 因为电话费随着通话时间的变化而变化,所以自变量是通话时间,因变量是电话费,故选B.
2.D 常量是固定不变的量,变量是变化的量,单价是不变的量,而金额是随着数量的变化而变化的,故选D.
3.D 故选D.
4.答案 是 不是
解析 根据函数的概念进行判断即可.
5.A 由题图可知,4时的气温最低,为-4℃;最高气温出现在12时之后,为8℃;最高气温比最低气温高12℃;0时至8时,气温先下降后上升.故选A.
6.C 根据题图可知,刚开始水面上升得比较快,然后越来越慢,故选C.
7.A 由题中表格可知y与x的函数关系式为y=-2x,将x=11代入y=-2x,得y=-22,故选A.
8.答案 (14.4,4.8)
解析 由题可知AB=8cm,BC=10cm,∵∠BAC=90°,∴由勾股定理得 6(cm),当AP⊥BC时, 解得AP=4.8cm,故点Q的纵坐标为4.8,此时由勾股定理得 所以点Q的横坐标为8+6.4=14.4,所以点Q的坐标为(14.4,4.8).
9.解析 (1)当x=2时,y=2×20-3=37,
当x=5时,y=5×20-4×3=88.
(2)由表格,得y=20x-(x-1)×3=17x+3.
(3)当y=1006时,17x+3=1006,解得x=59.
答:要使粘合后的总长度为1006cm,需用59张这样的卡纸.
能力提升
10.D 根据函数定义可知选D.
11.B 当x=1时,y=5+0.6;当x=2时,y=5×2+0.6×2;当x=3时,y=5×3+0.6×3;当x=4时,y=5×4+0.6×4,所以y=(5+0.6)x.故选B.
12.B 李叔叔开车上班,最初以某一速度匀速行驶,随着时间的增加,汽车行驶的路程逐渐增加,中途加油,随着时间的增加,汽车行驶的路程不变,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,随着时间的增加,汽车行驶的路程逐渐增加,并且比开始时增加得快.故选B.
13.C 汽车在乡村公路上行驶的速度为(270-180)÷(3.5-2)=60(km/h),,则该“脱贫攻坚”小组到达农村所用的时间为2+(360-180)÷60=5(h),故选C.
14.D 由题图②知,AB=BC=10,当BP⊥AC时,BP=8,此时, 6,∴AC=2PC=12,∴△ABC的面积 故选D.
15.答案 y=-6x+2
解析∵海拔每升高1千米,气温下降6℃,∴当海拔升高x千米时,气温下降6x℃.
故y=-6x+2.
16.答案 2
解析 因为3<4,所以把x=3代入y=|x|-1,得y=3-1=2.
17.C 由题图可知,经过1620年,镭的质量缩减为原来的 即 经过1620×2=3240年,镭的质量缩减为原来的 即 经过1620×3=4860年,镭的质量缩减为原来的 即 经过1620×4=6480年,镭的质量缩减为原来的 即 经过1620×5=8100年,镭的质量缩减为原来的 即32× 故选C.
18.答案 y=n+1+2
解析 根据题意得
第①个图:3=2+1=1+1+2 ,
第②个图:5=3+2=2+1+2 ,
第③个图:8=4+4=3+1+2 ,
第④个图:13=5+8=4+1+2 ,
……
以此类推,第 个图:y=n+1+2 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 一次函数
1 函数
基础过关
知识点1 函数的概念
1.2021年春节期间,疫情形势复杂,王丽遵循“防疫当前,本地过年”的原则,给远在家乡的亲人打电话拜年.电话费随着通话时间的变化而变化,在这个过程中,因变量是( )
A.王丽 B.电话费 C.通话时间 D.亲人
2.刘师傅到加油站加油,如图是所用的加油机上某一时刻的数据显示牌,则其中的变量是( )
A.金额 B.单价 C.数量 D.金额和数量
3.下列所描述的四个变化过程中,变量之间的关系不能看成函数关系的是( )
A.三角形的一个外角的度数x度和与它相邻的内角的度数y度的关系
B.树的高度为60厘米,每个月长高3厘米,x个月后,树的高度为y厘米,x与y的关系
C.正方形的面积y(平方厘米)和它的边长x(厘米)的关系
D.y是正数x的平方根,y与x之间的关系
4.若y=x ,则y________x的函数,x__________y的函数.(填“是”或“不是”)
知识点2 函数的表示方法
5.如图是某市一天的气温随时间变化的情况,下列说法正确的是( )
A.这一天的最低气温是-4℃ B.这一天12时的气温最高
C.最高气温比最低气温高8℃ D.0时至8时的气温呈下降趋势
6.用固定的速度往如图所示的杯子里注水,用x表示注水时间,y表示水杯底部到水面的高度,下列图象能大致表示y与x之间的关系的是( )
7.变量x,y的一些对应值如表:
x … -2 -1 0 1 2 3 …
y … 4 2 0 -2 -4 -6 …
根据表格中的数据规律,当x=11时,y的值是( )
A.-22 B.-11 C.11 D.22
8.如图①,在Rt△ABC中,∠BAC=90°,点P从点A出发,沿三角形的边以1cm/s的速度逆时针运动一周,图②是点P运动时,线段AP的长度y(cm)随运动时间x(s)变化的图象,其中Q是曲线部分的最低点,则点Q的坐标是_____________.
9.七年级二班制作文化墙时制作花边,需要将数张长为20cm,宽为8cm的长方形卡纸按如图所示的方式粘合起来,粘合部分的宽为3cm.
(1)根据题意,将下面的表格补充完整;
卡纸张数x(张) 1 2 3 4 5 …
纸条长度y(cm) 20 ____ 54 71 ____ …
(2)直接写出用x表示y的关系式:__________________;
(3)要使粘合后的总长度为1006cm,需用多少张这样的卡纸
能力提升
10.下列各图中,不能表示y是x的函数的是( )
11.已知x与y之间的关系如表所示:
x 1 2 3 4 …
y 5+0.6 10+1.2 15+1.8 20+2.4 …
下面的式子中,正确的是( )
12.李叔叔开车上班,最初以某一速度匀速行驶,中途停车加油耽误了几分钟,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,仍保持匀速行驶,则汽车行驶的路程y(千米)与行驶的时间t(小时)的函数关系的大致图象是( )
13.某“脱贫攻坚”小组乘汽车赴360km处的农村进行调研,前一段路为高速公路,后一段路为乡村公路,汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(km)与时间x(h)间的关系如图所示,则该“脱贫攻坚”小组到达农村所用的时间为( )
A.4 h B.4.5 h C.5 h D.5.5 h
14.如图①,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图②是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M是曲线部分的最低点,则△ABC的面积是( )
A.12 B.24 C.36 D.48
15.在登山过程中,海拔每升高1千米,气温下降6℃,已知某登山大本营所在的位置的气温是2℃,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是y℃,那么y关于x的函数表达式是_________________.
16.如图是一个运算程序示意图,若开始输入x的值为3,则输出y的值为__________.
17.[应用意识]实验证实,放射性物质在放出射线后,质量将减少,减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某种函数关系.
如图为表示镭的放射规律的函数图象,据此,32mg镭缩减为1mg所用的时间大约是( )
A.4860年 B.6480年 C.8100年 D.9720年
18.[几何直观]如图,从第一个三角形到第n个三角形,每个三角形中的三个数之间均具有相同的规律,按此规律,第n个三角形中,y与n之间的关系式是______________.
参考答案
基础过关
1.B 因为电话费随着通话时间的变化而变化,所以自变量是通话时间,因变量是电话费,故选B.
2.D 常量是固定不变的量,变量是变化的量,单价是不变的量,而金额是随着数量的变化而变化的,故选D.
3.D 故选D.
4.答案 是 不是
解析 根据函数的概念进行判断即可.
5.A 由题图可知,4时的气温最低,为-4℃;最高气温出现在12时之后,为8℃;最高气温比最低气温高12℃;0时至8时,气温先下降后上升.故选A.
6.C 根据题图可知,刚开始水面上升得比较快,然后越来越慢,故选C.
7.A 由题中表格可知y与x的函数关系式为y=-2x,将x=11代入y=-2x,得y=-22,故选A.
8.答案 (14.4,4.8)
解析 由题可知AB=8cm,BC=10cm,∵∠BAC=90°,∴由勾股定理得 6(cm),当AP⊥BC时, 解得AP=4.8cm,故点Q的纵坐标为4.8,此时由勾股定理得 所以点Q的横坐标为8+6.4=14.4,所以点Q的坐标为(14.4,4.8).
9.解析 (1)当x=2时,y=2×20-3=37,
当x=5时,y=5×20-4×3=88.
(2)由表格,得y=20x-(x-1)×3=17x+3.
(3)当y=1006时,17x+3=1006,解得x=59.
答:要使粘合后的总长度为1006cm,需用59张这样的卡纸.
能力提升
10.D 根据函数定义可知选D.
11.B 当x=1时,y=5+0.6;当x=2时,y=5×2+0.6×2;当x=3时,y=5×3+0.6×3;当x=4时,y=5×4+0.6×4,所以y=(5+0.6)x.故选B.
12.B 李叔叔开车上班,最初以某一速度匀速行驶,随着时间的增加,汽车行驶的路程逐渐增加,中途加油,随着时间的增加,汽车行驶的路程不变,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,随着时间的增加,汽车行驶的路程逐渐增加,并且比开始时增加得快.故选B.
13.C 汽车在乡村公路上行驶的速度为(270-180)÷(3.5-2)=60(km/h),,则该“脱贫攻坚”小组到达农村所用的时间为2+(360-180)÷60=5(h),故选C.
14.D 由题图②知,AB=BC=10,当BP⊥AC时,BP=8,此时, 6,∴AC=2PC=12,∴△ABC的面积 故选D.
15.答案 y=-6x+2
解析∵海拔每升高1千米,气温下降6℃,∴当海拔升高x千米时,气温下降6x℃.
故y=-6x+2.
16.答案 2
解析 因为3<4,所以把x=3代入y=|x|-1,得y=3-1=2.
17.C 由题图可知,经过1620年,镭的质量缩减为原来的 即 经过1620×2=3240年,镭的质量缩减为原来的 即 经过1620×3=4860年,镭的质量缩减为原来的 即 经过1620×4=6480年,镭的质量缩减为原来的 即 经过1620×5=8100年,镭的质量缩减为原来的 即32× 故选C.
18.答案 y=n+1+2
解析 根据题意得
第①个图:3=2+1=1+1+2 ,
第②个图:5=3+2=2+1+2 ,
第③个图:8=4+4=3+1+2 ,
第④个图:13=5+8=4+1+2 ,
……
以此类推,第 个图:y=n+1+2 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
