2022-2023学年人教版 九年级数学上册 24.3 正多边形和圆 训练试卷(含答案)
文档属性
| 名称 | 2022-2023学年人教版 九年级数学上册 24.3 正多边形和圆 训练试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 456.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-13 00:00:00 | ||
图片预览

文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
第二十四章 圆
24.3 正多边形和圆
一、选择题
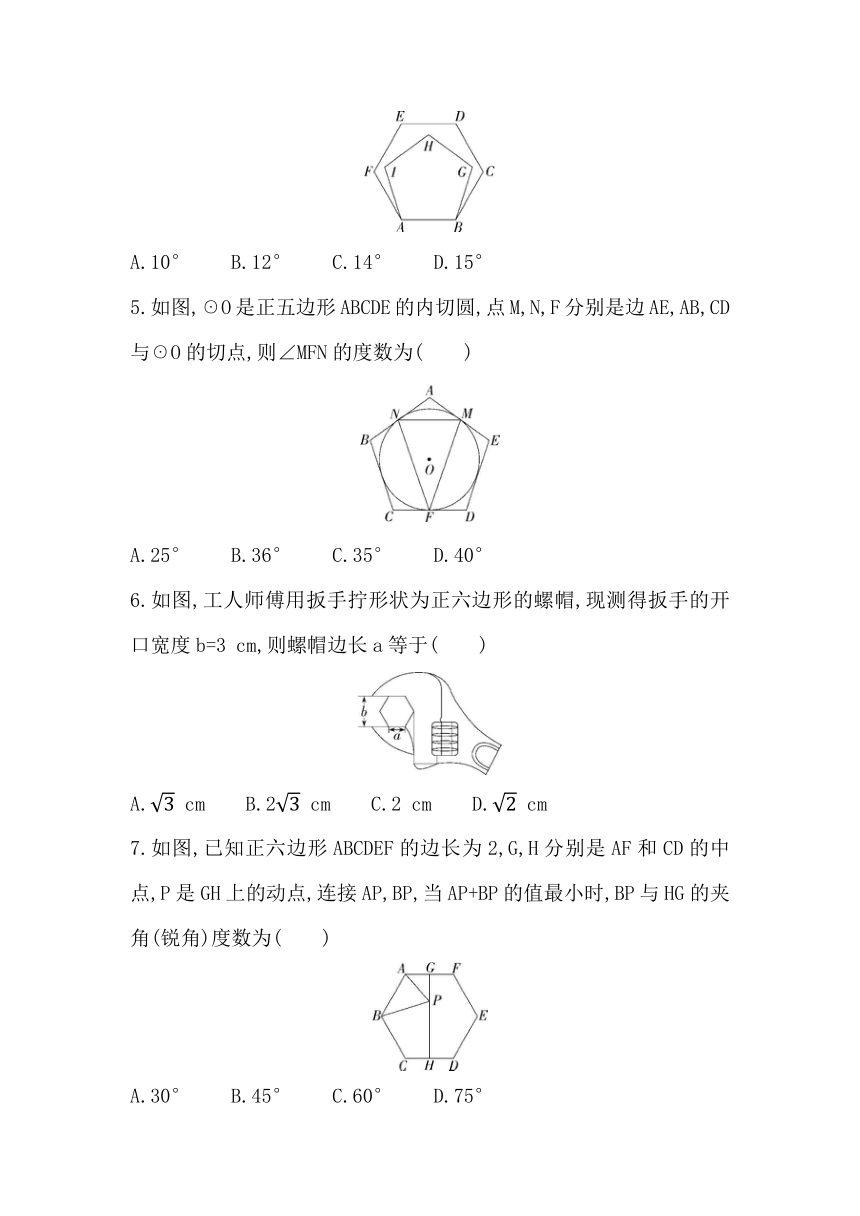
1. 如图,☉O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是( )
A.144° B.130° C.129° D.108°
2. 一个圆的内接正六边形与内接正方形的边长之比为( )
A.3∶2 B.1∶ C.1∶ D.∶
3. 10个大小相同的正六边形按如图所示的方式紧密排列在同一平面内,A、B、C、D、E、O均是正六边形的顶点,则点O是下列哪个三角形的外心( )
A.△AED B.△ABD C.△BCD D.△ACD
4.如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠FAI=( )
A.10° B.12° C.14° D.15°
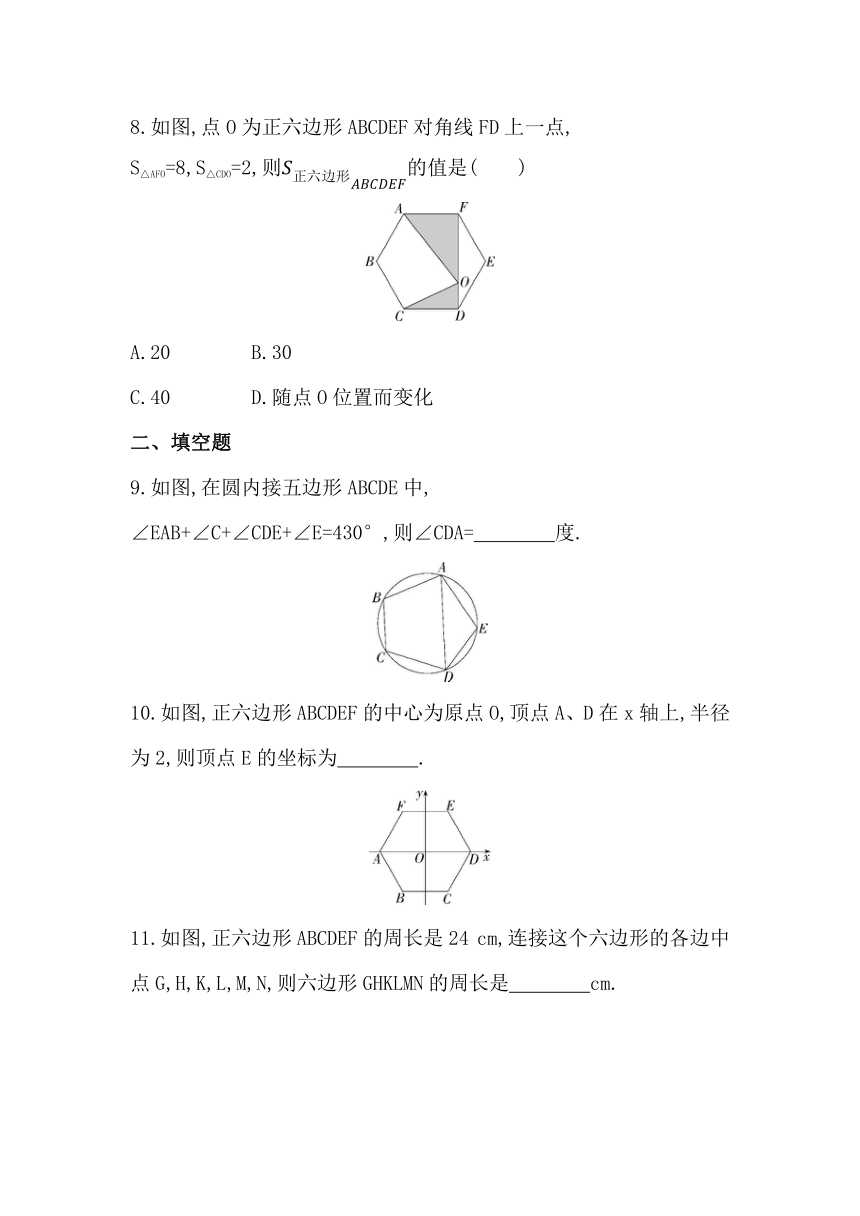
5.如图,☉O是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与☉O的切点,则∠MFN的度数为( )
A.25° B.36° C.35° D.40°
6.如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度b=3 cm,则螺帽边长a等于( )
A. cm B.2 cm C.2 cm D. cm
7.如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,当AP+BP的值最小时,BP与HG的夹角(锐角)度数为( )
A.30° B.45° C.60° D.75°
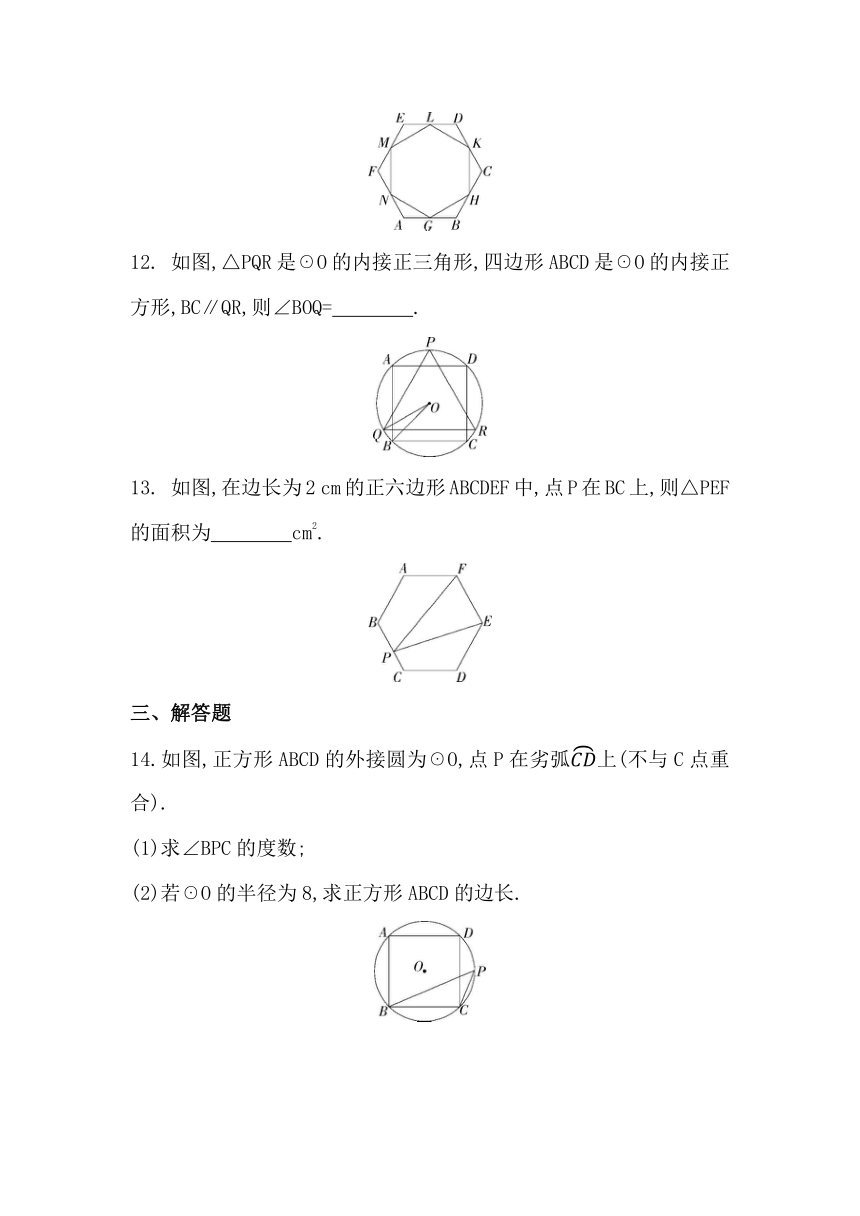
8.如图,点O为正六边形ABCDEF对角线FD上一点,
S△AFO=8,S△CDO=2,则的值是( )
A.20 B.30
C.40 D.随点O位置而变化
二、填空题
9.如图,在圆内接五边形ABCDE中,
∠EAB+∠C+∠CDE+∠E=430°,则∠CDA= 度.
10.如图,正六边形ABCDEF的中心为原点O,顶点A、D在x轴上,半径为2,则顶点E的坐标为 .
11.如图,正六边形ABCDEF的周长是24 cm,连接这个六边形的各边中点G,H,K,L,M,N,则六边形GHKLMN的周长是 cm.
12. 如图,△PQR是☉O的内接正三角形,四边形ABCD是☉O的内接正方形,BC∥QR,则∠BOQ= .
13. 如图,在边长为2 cm的正六边形ABCDEF中,点P在BC上,则△PEF的面积为 cm2.
三、解答题
14.如图,正方形ABCD的外接圆为☉O,点P在劣弧上(不与C点重合).
(1)求∠BPC的度数;
(2)若☉O的半径为8,求正方形ABCD的边长.
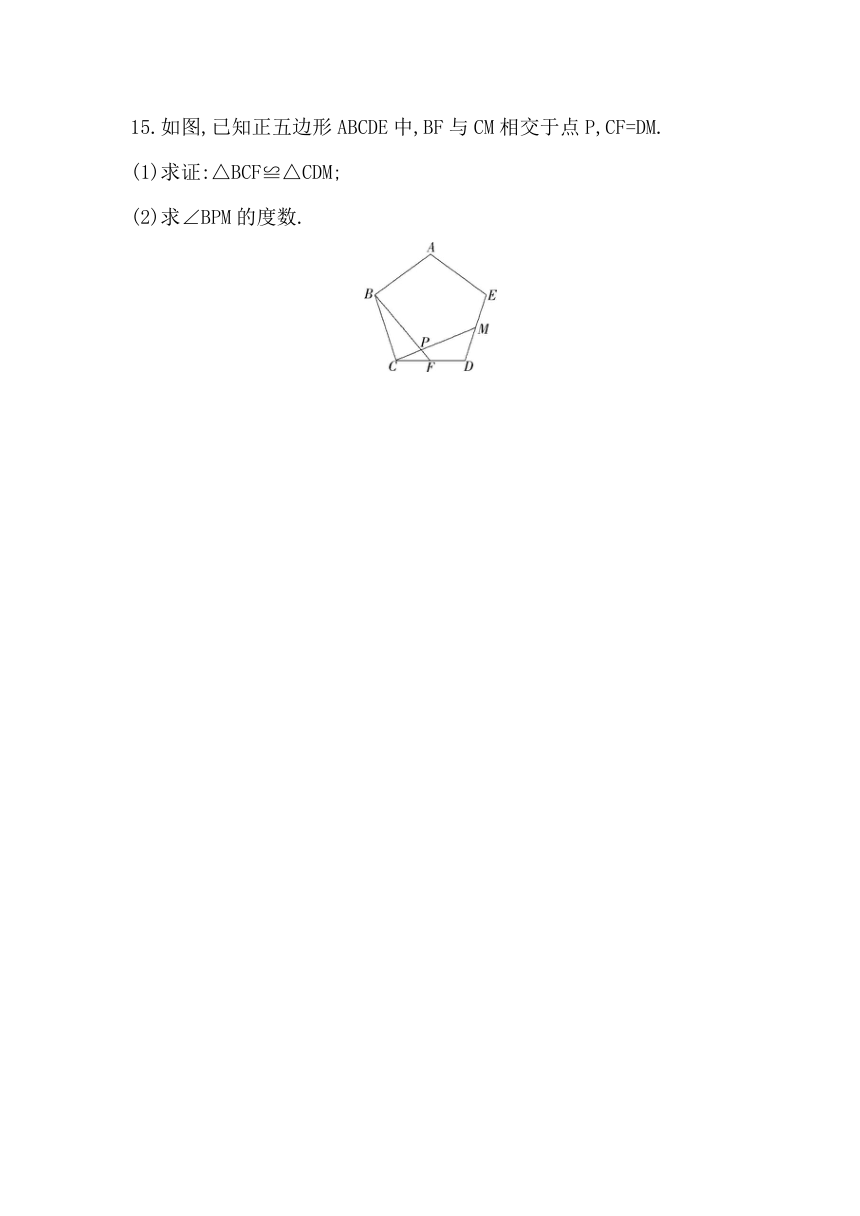
15.如图,已知正五边形ABCDE中,BF与CM相交于点P,CF=DM.
(1)求证:△BCF≌△CDM;
(2)求∠BPM的度数.
答案全解全析
一、选择题
1.答案 A ∵正五边形的一个内角=(5-2)×180°÷5=108°,
∴∠E=∠D=108°,∵AE、CD分别与☉O相切于A、C两点,
∴∠OAE=∠OCD=90°,∴∠AOC=(5-2)×180°-90°-90°-108°-108°=144°.故选A.
2.答案 C 设此圆的半径为R,则它的内接正六边形的边长为R,它的内接正方形的边长为R,所以这个圆的内接正六边形与内接正方形的边长之比为R∶R=1∶.故选C.
3.答案 D 连接OA、OB、OC、OD、OE,有OA=OC=OD,∵三角形的外心到三角形的三个顶点的距离相等,∴点O是△ACD的外心.故选D.
4. 答案 B 在正六边形ABCDEF和正五边形ABGHI中,∠FAB=120°,∠IAB=108°,
∴∠FAI=∠FAB-∠IAB=120°-108°=12°.
5. 答案 B 如图,连接OM,ON.∵M,N分别是AE,AB与☉O的切点,∴OM⊥AE,ON⊥AB,∴∠OMA=∠ONA=90°.∵∠A=108°,
∴∠MON=180°-108°=72°,∴∠MFN=∠MON=36°.
6. 答案 A 如图,连接AC,过点B作BD⊥AC于D,由题意得∠ABC=120°,AB=BC=a,
∴∠BCD=∠BAC=30°,由AC=3,得AD=CD=1.5,∵Rt△ABD中,∠BAD=30°,∴BD=AB=a,∴AD==a,即a=1.5,∴a=(cm).故选A.
答案 C 如图,连接PF,BF,BF交GH于点P',连接AP'.∵正六边形ABCDEF中,G,H分别是AF和CD的中点,∴直线GH是正六边形的对称轴,
∴PA=PF,∴PA+PB=PF+PB.∵PB+PF≥BF,
∴当点P与点P'重合时,PA+PB的值最小.
∵∠BAF=120°,AB=AF,∴∠ABF=∠AFB=30°.
∵∠FGP'=90°,∴∠FP'G=60°,即∠BP'H=60°.故选C.
答案 B 如图,设正六边形ABCDEF的中心为G,连接GC,GD,GE,GF,AC.易得△EFG,△DEG和△CDG都是等边三角形,且大小相同,点C,G,F在同一条直线上,则S△CDG=S△DFG=S正六边形ABCDEF.易得四边形ACDF是矩形,
∵S△AFO=8,S△CDO=2,∴=2×(8+2)=20,∴S△CDG=S矩形ACDF=5,
∴S正六边形ABCDEF=6S△CDG=30.
二、填空题
9.答案 70
解析 ∵五边形ABCDE的内角和为(5-2)×180°=540°,
∴∠EAB+∠B+∠C+∠CDE+∠E=540°.∵∠EAB+∠C+∠CDE+∠E=430°,
∴∠B=540°-430°=110°.∵四边形ABCD为☉O的内接四边形,
∴∠B+∠CDA=180°,∴∠CDA=180°-110°=70°.
10.答案 (1,)
解析 如图,连接OE,由正六边形是轴对称图形知,在Rt△OEG中,
∠GOE=30°,∵OE=2,∴GE=1,OG=.∴E(1,).
11.答案 12
解析 如图,设正六边形ABCDEF的中心为O,连接OG,OA,OB.∵正六边形ABCDEF的周长是24 cm,∴OA=OB=AB=×24=4(cm).∵点G是AB的中点,
∴∠AGO=90°,AG=2 cm,由勾股定理得OG=2(cm).
∵顺次连接正六边形ABCDEF各边的中点G、H、K、L、M、N得到的六边形为正六边形,O为正六边形GHKLMN的中心,∴NG=OG=2 cm,∴六边形GHKLMN的周长是2×6=12(cm).
12. 答案 15°
解析 如图,连接OA,OD,OP,∵△PQR是☉O的内接正三角形,∴PQ=PR=QR,
∴∠POQ=×360°=120°.∵BC∥QR,OP⊥QR,∴OP⊥BC.
∵四边形ABCD是☉O的内接正方形,
∴OP⊥AD,∠AOD=90°,
∴=,∴∠AOP=∠DOP,∴∠AOP=×90°=45°,
∴∠AOQ=∠POQ-∠AOP=75°.∵∠AOB=90°,∴∠QOB=15°.
13. 答案 2
解析 如图,连接BF,BE,过点A作AT⊥BF于T,
∵六边形ABCDEF是正六边形,
∴CB∥EF,AB=AF,∠BAF=120°,
∴S△PEF=S△BEF.∵AT⊥BF,AB=AF,
∴BT=FT,∠BAT=∠FAT=60°,∴∠ABT=30°,
∴AT=AB=1 cm,∴BT= cm.
∴BF=2BT=2 cm,
∵∠AFE=120°,∠AFB=∠ABF=30°,
∴∠BFE=90°,
∴S△PEF=S△BEF=EF·BF=×2×2=2(cm2).
三、解答题
14.解析 (1)如图,连接OB,OC.
∵四边形ABCD为正方形,∴∠BOC=90°,
∴∠BPC=∠BOC=45°.
(2)如图,过点O作OE⊥BC于点E,
∵OB=OC,∠BOC=90°,
∴∠OBE=45°,∵OE⊥BC,∴OE=BE,
∵OE2+BE2=OB2,∴BE===4,
∴BC=2BE=2×4=8,即正方形ABCD的边长为8.
15.解析 (1)证明:∵五边形ABCDE是正五边形,
∴BC=CD,∠BCF=∠CDM.
在△BCF和△CDM中,
∴△BCF≌△CDM.
(2)∵五边形ABCDE是正五边形,
∴∠BCF==108°,
∴∠CBF+∠CFB=180°-∠BCF=72°,
∵△BCF≌△CDM,∴∠MCD=∠CBF,
∴∠MCD+∠CFB=72°,
∴∠BPM=∠CPF=180°-(∠MCD+∠CFB)=108°.
班级 姓名
第二十四章 圆
24.3 正多边形和圆
一、选择题
1. 如图,☉O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是( )
A.144° B.130° C.129° D.108°
2. 一个圆的内接正六边形与内接正方形的边长之比为( )
A.3∶2 B.1∶ C.1∶ D.∶
3. 10个大小相同的正六边形按如图所示的方式紧密排列在同一平面内,A、B、C、D、E、O均是正六边形的顶点,则点O是下列哪个三角形的外心( )
A.△AED B.△ABD C.△BCD D.△ACD
4.如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠FAI=( )
A.10° B.12° C.14° D.15°
5.如图,☉O是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与☉O的切点,则∠MFN的度数为( )
A.25° B.36° C.35° D.40°
6.如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度b=3 cm,则螺帽边长a等于( )
A. cm B.2 cm C.2 cm D. cm
7.如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,当AP+BP的值最小时,BP与HG的夹角(锐角)度数为( )
A.30° B.45° C.60° D.75°
8.如图,点O为正六边形ABCDEF对角线FD上一点,
S△AFO=8,S△CDO=2,则的值是( )
A.20 B.30
C.40 D.随点O位置而变化
二、填空题
9.如图,在圆内接五边形ABCDE中,
∠EAB+∠C+∠CDE+∠E=430°,则∠CDA= 度.
10.如图,正六边形ABCDEF的中心为原点O,顶点A、D在x轴上,半径为2,则顶点E的坐标为 .
11.如图,正六边形ABCDEF的周长是24 cm,连接这个六边形的各边中点G,H,K,L,M,N,则六边形GHKLMN的周长是 cm.
12. 如图,△PQR是☉O的内接正三角形,四边形ABCD是☉O的内接正方形,BC∥QR,则∠BOQ= .
13. 如图,在边长为2 cm的正六边形ABCDEF中,点P在BC上,则△PEF的面积为 cm2.
三、解答题
14.如图,正方形ABCD的外接圆为☉O,点P在劣弧上(不与C点重合).
(1)求∠BPC的度数;
(2)若☉O的半径为8,求正方形ABCD的边长.
15.如图,已知正五边形ABCDE中,BF与CM相交于点P,CF=DM.
(1)求证:△BCF≌△CDM;
(2)求∠BPM的度数.
答案全解全析
一、选择题
1.答案 A ∵正五边形的一个内角=(5-2)×180°÷5=108°,
∴∠E=∠D=108°,∵AE、CD分别与☉O相切于A、C两点,
∴∠OAE=∠OCD=90°,∴∠AOC=(5-2)×180°-90°-90°-108°-108°=144°.故选A.
2.答案 C 设此圆的半径为R,则它的内接正六边形的边长为R,它的内接正方形的边长为R,所以这个圆的内接正六边形与内接正方形的边长之比为R∶R=1∶.故选C.
3.答案 D 连接OA、OB、OC、OD、OE,有OA=OC=OD,∵三角形的外心到三角形的三个顶点的距离相等,∴点O是△ACD的外心.故选D.
4. 答案 B 在正六边形ABCDEF和正五边形ABGHI中,∠FAB=120°,∠IAB=108°,
∴∠FAI=∠FAB-∠IAB=120°-108°=12°.
5. 答案 B 如图,连接OM,ON.∵M,N分别是AE,AB与☉O的切点,∴OM⊥AE,ON⊥AB,∴∠OMA=∠ONA=90°.∵∠A=108°,
∴∠MON=180°-108°=72°,∴∠MFN=∠MON=36°.
6. 答案 A 如图,连接AC,过点B作BD⊥AC于D,由题意得∠ABC=120°,AB=BC=a,
∴∠BCD=∠BAC=30°,由AC=3,得AD=CD=1.5,∵Rt△ABD中,∠BAD=30°,∴BD=AB=a,∴AD==a,即a=1.5,∴a=(cm).故选A.
答案 C 如图,连接PF,BF,BF交GH于点P',连接AP'.∵正六边形ABCDEF中,G,H分别是AF和CD的中点,∴直线GH是正六边形的对称轴,
∴PA=PF,∴PA+PB=PF+PB.∵PB+PF≥BF,
∴当点P与点P'重合时,PA+PB的值最小.
∵∠BAF=120°,AB=AF,∴∠ABF=∠AFB=30°.
∵∠FGP'=90°,∴∠FP'G=60°,即∠BP'H=60°.故选C.
答案 B 如图,设正六边形ABCDEF的中心为G,连接GC,GD,GE,GF,AC.易得△EFG,△DEG和△CDG都是等边三角形,且大小相同,点C,G,F在同一条直线上,则S△CDG=S△DFG=S正六边形ABCDEF.易得四边形ACDF是矩形,
∵S△AFO=8,S△CDO=2,∴=2×(8+2)=20,∴S△CDG=S矩形ACDF=5,
∴S正六边形ABCDEF=6S△CDG=30.
二、填空题
9.答案 70
解析 ∵五边形ABCDE的内角和为(5-2)×180°=540°,
∴∠EAB+∠B+∠C+∠CDE+∠E=540°.∵∠EAB+∠C+∠CDE+∠E=430°,
∴∠B=540°-430°=110°.∵四边形ABCD为☉O的内接四边形,
∴∠B+∠CDA=180°,∴∠CDA=180°-110°=70°.
10.答案 (1,)
解析 如图,连接OE,由正六边形是轴对称图形知,在Rt△OEG中,
∠GOE=30°,∵OE=2,∴GE=1,OG=.∴E(1,).
11.答案 12
解析 如图,设正六边形ABCDEF的中心为O,连接OG,OA,OB.∵正六边形ABCDEF的周长是24 cm,∴OA=OB=AB=×24=4(cm).∵点G是AB的中点,
∴∠AGO=90°,AG=2 cm,由勾股定理得OG=2(cm).
∵顺次连接正六边形ABCDEF各边的中点G、H、K、L、M、N得到的六边形为正六边形,O为正六边形GHKLMN的中心,∴NG=OG=2 cm,∴六边形GHKLMN的周长是2×6=12(cm).
12. 答案 15°
解析 如图,连接OA,OD,OP,∵△PQR是☉O的内接正三角形,∴PQ=PR=QR,
∴∠POQ=×360°=120°.∵BC∥QR,OP⊥QR,∴OP⊥BC.
∵四边形ABCD是☉O的内接正方形,
∴OP⊥AD,∠AOD=90°,
∴=,∴∠AOP=∠DOP,∴∠AOP=×90°=45°,
∴∠AOQ=∠POQ-∠AOP=75°.∵∠AOB=90°,∴∠QOB=15°.
13. 答案 2
解析 如图,连接BF,BE,过点A作AT⊥BF于T,
∵六边形ABCDEF是正六边形,
∴CB∥EF,AB=AF,∠BAF=120°,
∴S△PEF=S△BEF.∵AT⊥BF,AB=AF,
∴BT=FT,∠BAT=∠FAT=60°,∴∠ABT=30°,
∴AT=AB=1 cm,∴BT= cm.
∴BF=2BT=2 cm,
∵∠AFE=120°,∠AFB=∠ABF=30°,
∴∠BFE=90°,
∴S△PEF=S△BEF=EF·BF=×2×2=2(cm2).
三、解答题
14.解析 (1)如图,连接OB,OC.
∵四边形ABCD为正方形,∴∠BOC=90°,
∴∠BPC=∠BOC=45°.
(2)如图,过点O作OE⊥BC于点E,
∵OB=OC,∠BOC=90°,
∴∠OBE=45°,∵OE⊥BC,∴OE=BE,
∵OE2+BE2=OB2,∴BE===4,
∴BC=2BE=2×4=8,即正方形ABCD的边长为8.
15.解析 (1)证明:∵五边形ABCDE是正五边形,
∴BC=CD,∠BCF=∠CDM.
在△BCF和△CDM中,
∴△BCF≌△CDM.
(2)∵五边形ABCDE是正五边形,
∴∠BCF==108°,
∴∠CBF+∠CFB=180°-∠BCF=72°,
∵△BCF≌△CDM,∴∠MCD=∠CBF,
∴∠MCD+∠CFB=72°,
∴∠BPM=∠CPF=180°-(∠MCD+∠CFB)=108°.
同课章节目录
